1478. 安排邮筒||邮递员问题（dp绝对值不等式）

给你一个房屋数组houses 和一个整数 k ，其中 houses[i] 是第 i 栋房子在一条街上的位置，现需要在这条街上安排 k 个邮筒。

请你返回每栋房子与离它最近的邮筒之间的距离的 最小 总和。

答案保证在 32 位有符号整数范围以内。

 

示例 1：

 

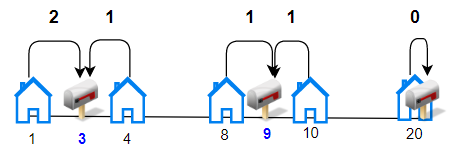
输入：houses = [1,4,8,10,20], k = 3
输出：5
解释：将邮筒分别安放在位置 3， 9 和 20 处。
每个房子到最近邮筒的距离和为 |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5 。

示例 2：

 

 

 

输入：houses = [2,3,5,12,18], k = 2
输出：9
解释：将邮筒分别安放在位置 3 和 14 处。
每个房子到最近邮筒距离和为 |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9 。
示例 3：

输入：houses = [7,4,6,1], k = 1
输出：8
示例 4：

输入：houses = [3,6,14,10], k = 4
输出：0
 

提示：

n == houses.length
1 <= n <= 100
1 <= houses[i] <= 10^4
1 <= k <= n
数组 houses 中的整数互不相同。

这个题就是说给你一排房子，然后给你m个邮箱可以房子，你可以随意安排位置，求每一个房子到离它最近的邮箱的距离总和的最小值

 

首先我们先考虑一个问题就是假如给你n个房子的坐标，然后你只能有一个邮箱怎么求这个最小的距离总和呢？

这个问题涉及到绝对值不等式，就是先拍个序，然后求这个中位数(a[(1+n)/2)然后每一个数，跟他做差求和就是答案

 

然后这个题是一个dp，f[i][j]数组代表的是前i个数组，分到j个邮箱的最小值

然后我们一层枚举i，一层枚举j，然后一层枚举枚举这一段的起点

然后转移方程就是转移时，对于 i 和 j，枚举当前段的起点 l，令闭区间 [l, i] 使用同一个邮筒，则转移 f(i,j)=min(f(l−1,j−1)+cost(l,i))。

然后这个题要预先处理出来cost[i][j]就是从i到j共用一个邮箱的话，最小花费

class Solution {
public:
    int minDistance(vector<int>& h, int m) {
        sort(h.begin(),h.end());
        int n=h.size();
        vector<vector<int>> f(n, vector<int>(m + 1));
        vector<vector<int>> cost(n, vector<int>(n));
        for(int i=0;i<n;i++){
            for(int j=i;j<n;j++){
                for(int k=i;k<=j;k++){
                    cost[i][j] += abs(h[k] - h[i + (j - i + 1) / 2]);
                }
            }
        }
        for (int i = 0; i < n; i ++ ) f[i][0] = 1e8;
        for(int i=1;i<n;i++){
            for(int j=1;j<=m;j++){
                f[i][j]=1e8;
                for(int k=0;k<=i;k++){
                    int t=0;
                    if(k) t=f[k-1][j-1];
                    f[i][j]=min(f[i][j],t+cost[k][i]);
                }
            }
        }
        return f[n-1][m];
    }
};