1463. 摘樱桃 II(dp)
给你一个 rows x cols 的矩阵 grid 来表示一块樱桃地。 grid 中每个格子的数字表示你能获得的樱桃数目。
你有两个机器人帮你收集樱桃,机器人 1 从左上角格子 (0,0) 出发,机器人 2 从右上角格子 (0, cols-1) 出发。
请你按照如下规则,返回两个机器人能收集的最多樱桃数目:
从格子 (i,j) 出发,机器人可以移动到格子 (i+1, j-1),(i+1, j) 或者 (i+1, j+1) 。
当一个机器人经过某个格子时,它会把该格子内所有的樱桃都摘走,然后这个位置会变成空格子,即没有樱桃的格子。
当两个机器人同时到达同一个格子时,它们中只有一个可以摘到樱桃。
两个机器人在任意时刻都不能移动到 grid 外面。
两个机器人最后都要到达 grid 最底下一行。
示例 1:
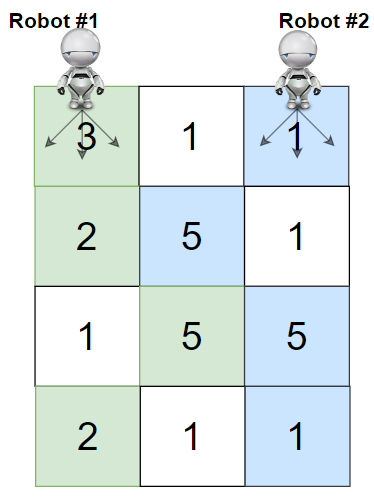



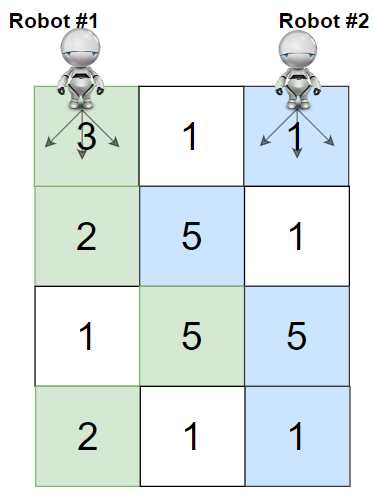
输入:grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
输出:24
解释:机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (3 + 2 + 5 + 2) = 12 。
机器人 2 摘的樱桃数目为 (1 + 5 + 5 + 1) = 12 。
樱桃总数为: 12 + 12 = 24 。
示例 2:
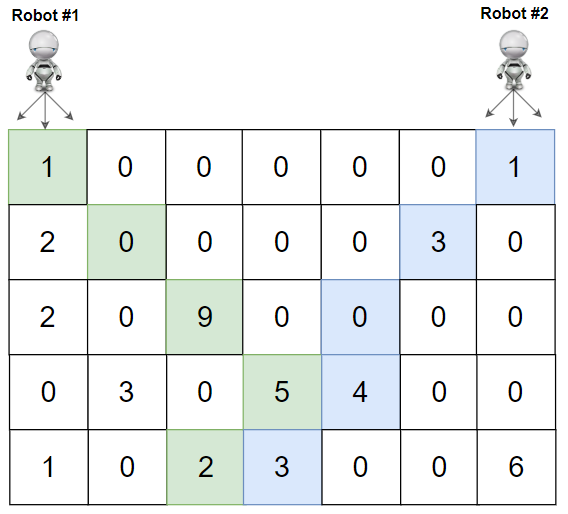
输入:grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
输出:28
解释:机器人 1 和机器人 2 的路径在上图中分别用绿色和蓝色表示。
机器人 1 摘的樱桃数目为 (1 + 9 + 5 + 2) = 17 。
机器人 2 摘的樱桃数目为 (1 + 3 + 4 + 3) = 11 。
樱桃总数为: 17 + 11 = 28 。
示例 3:
输入:grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]
输出:22
示例 4:
输入:grid = [[1,1],[1,1]]
输出:4
提示:
rows == grid.length
cols == grid[i].length
2 <= rows, cols <= 70
0 <= grid[i][j] <= 100
这个题就是说给,两个人一个在(0,0),一个在(0,m-1)就是他们两个都只能向左下,右下,向下走,如果你个人走到了(i,j)那么他就会把a[i][j]的樱桃都拿掉
就是问两个人能摘的樱桃的最大值,如果两个人同时走到a[i][j]只能得到一个a[i][j]
这个题你会发现两个人只要走一步都会向下一层
状态表示:
f[k,i,j]:两个机器人从各自起点分别到达(k,i),(k,j)时获得的樱桃数目的最大值
状态计算:
当机器人1到达(k,i)点时,可以从(k- 1,i - 1),(k- 1,i ),(k- 1,i + 1)点走过来
当机器人2到达(k,j)点时,可以从(k-1,j-1),(k - 1,j),(k - 1,j + 1)点走过来
因此 f[k,i,j] 可以从 f[k- 1,x1,x2] 转移过来,j1 - 1<= x1 <= j1 + 1,j2 - 1<= x2 <= j2 + 1
转移过程中
若i == j,表示在落在同一个地方,f[k,i,j] = f[k- 1,x1,x2] + grid[k,i]
若i != j,表示在落在不同地方,f[k,i,j] = f[k - 1,x1,x2] + grid[k,i] + grid[k,j]
初始化:第0层获得的数目是一定的,即f[0][0][m - 1] = grid[0][0] + grid[0][m - 1],为了避免其他点从无效状态转移过来,若按0处理,容易造成比最优情况值还要大,导致错误,因此需要将无效状态全部赋值为负无穷大
最终值:枚举两个机器人分别落在最后一行的全部位置,算出最大值
class Solution { public: int cherryPickup(vector<vector<int>>& grid) { int n = grid.size(), m = grid[0].size();//行和列 vector<vector<vector<int>>> f(n, vector<vector<int>>(m, vector<int>(m, -1))); f[0][0][m-1]=grid[0][0]+grid[0][m-1]; int ans=0; for(int k=1;k<n;k++){ for(int i=0;i<m;i++){ for(int j=0;j<m;j++){ for(int x=i-1;x<=i+1;x++){ for(int y=j-1;y<=j+1;y++){ if(x<0||x>=m||y<0||y>=m){ continue; } int t=f[k-1][x][y];//这是代表的从(x,y)->(i,j), if(t==-1){ continue; } if(i==j){ t+=grid[k][j]; } else{ t+=grid[k][i]+grid[k][j]; } f[k][i][j]=max(f[k][i][j],t); ans=max(ans,f[k][i][j]); } } } } } return ans; } };
这个题和传纸条的很相似



 浙公网安备 33010602011771号
浙公网安备 33010602011771号