数论分块

 

 Sample Input

11

1

2

3

4

5

6

7

8

9

10

2147483647

Sample Output

Case 1: 1

Case 2: 3

Case 3: 5

Case 4: 8

Case 5: 10

Case 6: 14

Case 7: 16

Case 8: 20

Case 9: 23

Case 10: 27

Case 11: 46475828386

题意：就是让你求[n/i]在1到n上的和，n是1e9所以不能暴力，要用数论分块

 

//要找到是[n/i]==[n/j]中的最大的j;
//j=[n/[n/i]]

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
/*
要找到是[n/i]==[n/j]中的最大的j;
j=[n/[n/i]]
 */
int main(){
    ll n;
    int t;
    cin>>t;
    int kase=1;
    while(t--){
        cin>>n;
        ll ans=0;
        ll l,r;
        for(l=1;l<=n;l=r+1){
            if(n/l==0){
                break;
            }
            r=min(n,n/(n/l));
            ans+=(n/l)*(r-l+1);
        }
        printf("Case %d: %lld\n",kase++,ans);
    }
}

 

 

 

 

 

 

例二：求余数和

 传送门

根据 k mod i = k - floor(k / i ) i,可将j(n,k)转化成如下式子：
f(n,k) = k mod 1+ k mod 2 + …k mod n
　　　 = k - floor(k/1) * 1 + k - floor(k/2) * 2+… k - floor(k /n) n
　　　 = n * k - sum(floor(k/i) * i) 其中 i = 1~ n

 

 

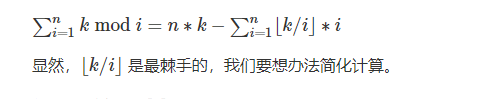
#include <cstdio>
#include <iostream>
using namespace std;
typedef long long LL;
int n, k, l, r;
LL ans;
int main() {
    scanf("%d%d", &n, &k);
    ans = (LL)n * k;
    for (l = 1; l <= n; l = r + 1) {
        if(k / l == 0) break;
        r = min(k / (k / l), n);
        ans -= (LL)(k / l) * (l + r) * (r - l + 1) / 2;
    }
    printf("%lld\n", ans);
    return 0;
}

 

例三：
链接：https://ac.nowcoder.com/acm/contest/11160/C
来源：牛客网

小G定义了两个函数F(n)为n的约数和，G(n)为F(1)+F(2)+...+F(n-1)+F(n)
小G想知道G(G(n))等于多少

输入描述:

小G会给你一个n

输出描述:

输出一个数G(G(n))即可

示例1

输入

复制

5

输出

复制

371

备注:

数据范围:
1<=n<=5e4

 

 这个题就是数论分块。

#include<iostream>
#include<algorithm>
typedef long long ll; 
/*

小G定义了两个函数F(n)为n的约数和，G(n)为F(1)+F(2)+...+F(n-1)+F(n)
小G想知道G(G(n))等于多少
*/
using namespace std;
ll G(ll n){
    ll sum=0;
    ll i,j;
    for(i=1;i<=n;i=j+1){
        if(n/i==0){
            break;
        }
        j=min(n,n/(n/i));
        ll z=((j-i+1)*(i+j))/2;
        sum+=(n/i)*z;
    }
    return sum;
}
int main(){
    ll n;
    cin>>n;
    cout<<G(G(n))<<endl;
    return 0;
} 

 

 

 

 

 

 

 

 

 

 

 

 这个题的题意就是求l到r中的所有数的因子和的和

这个题和上面的都是一样的思路

ll f(ll n)//除法分块+等差数列求
{
    ll left,right;
    ll sum=0;//l 到 r中的因子不同但是个数相同都是n/left 
    for(left=1;left<=n;left=right+1)//分块算因子和
    {
        right=n/(n/left);
        sum +=(n/left)*(left+right)*(right-left+1)/2;//等差数列公式
    }
    return sum;
}

n/left指的是区间[l,r]中的所有数的因子个数都有n/left个

就是l这个因子有n/left个，l+1这个因子有n/left个-----------r这个因子有n/left个

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;//必须是unsigned
ll f(ll n)//除法分块+等差数列求
{
    ll left,right;
    ll sum=0;//l 到 r中的因子不同但是个数相同都是n/left 
    for(left=1;left<=n;left=right+1)//分块算因子和
    {
        right=n/(n/left);
        sum +=(n/left)*(left+right)*(right-left+1)/2;//等差数列公式
    }
    return sum;
}
int main()
{
    ll a,b;
    cin>>a>>b;
    cout<<f(b)-f(a-1)<<endl;
    return 0;
}

题目链接 

 

 

输入输出样例

输入 #1复制

2 4

输出 #1复制

7

这个题你首先看看这个是不是很熟悉？
没错他就是x的因子个数
就是求a-b区间的每一个数的因子的个数和
那么就是分块中的l-r中的每一个因子都出现了n/l次所以就是出现了n/l*(r-l+1)次

#include<iostream>
#include<algorithm>
#include<map>
#include<cstring>
#include<vector>
using namespace std;
typedef long long ll;
const int maxn=3e6+100;
const int mod=998244353;
ll solve(ll n){
    ll l,r;//数论分块
    ll ans=0; 
    for(l=1;l<=n;l=r+1){
        r=n/(n/l); 
        ans=(ans+(r-l+1)*(n/l))%mod;
    }
    return ans;
}
int main(){
    ll l,r;
    cin>>l>>r;
    cout<<(solve(r)-solve(l-1)+mod)%mod<<endl;
}