【bzoj2402】陶陶的难题II

题目

题解

分数规划+树链剖分+维护凸壳

神题

所求答案是分数的形式，一眼分数规划。

二分mid后问题转化为判断 $y_i+q_j−mid(x_i+p_j)$ 的最大值是否大于0。

整理得 $(y_i−mid⋅x_i)+(q_j−mid⋅p_j) $最大，此时可以发现i 和 j不再有关系，分开考虑最大值。

对于这种树上路径问题，一般先通过树剖转成序列问题

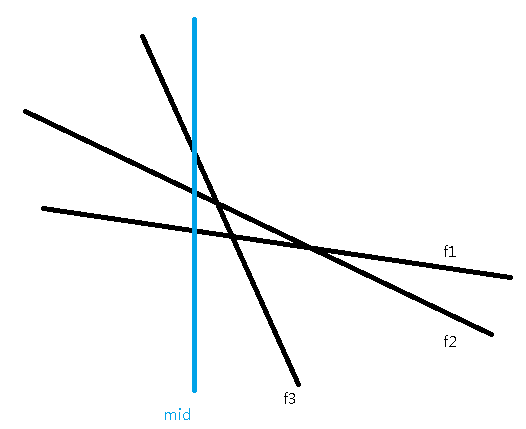
观察$y_i−mid⋅x_i$可以看作一个函数：$f(mid)=-mid⋅x_i+y_i$

即把每个点变成一个函数

那么对于每一个询问，求得就是指定区间中的函数的自变量为当前二分的mid时时最大的函数值（如下图）

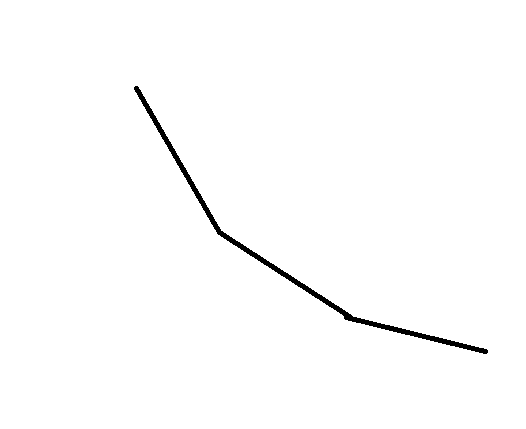
那么就在线段树的每个节点维护对应区间的函数所构成的一个这样的凸壳（这些函数都是单调递减的）

 

 那么用半平面交处理即可

具体的话就是每次合并的时候，按斜率归并排序

然后跑半平面交即可

预处理这个只需要$O(nlogn^2)$

 每次询问二分这个凸壳（看mid在哪两个交点中间）即可

时间复杂度为$O(nlogn^2+nlogn^4)$（放心，能过）

代码

#include <algorithm>
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
#define point line
#define N 300000
#define lc id*2
#define rc id*2+1
#define add(a) lines[id].push_back(a),pts[id].push_back(inter(a,lines[id][c++]))
#define half (l+r)/2
double x[N],y[N],p[N],q[N];
struct line
{
	double a,b;
	line(double c,double d):a(c),b(d){};
};
bool operator >(line a,line b)
{
	return a.a==b.a?(a.b>b.b):(a.a>b.a);
}
bool operator <(point a,double b)
{
	return a.a<b;
}
line operator -(line a,line b)
{
	return line(a.a-b.a,a.b-b.b);
}
double operator *(point a,point b)
{
	return a.a*b.b-a.b*b.a;
}
point inter(line a,line b)
{
	double x=(b.b-a.b)/(a.a-b.a);
	return point(x,a.a*x+a.b);
}
vector<int> vec[N];
vector<line> lines1[N],lines2[N];
vector<point> pts1[N],pts2[N];
int bigson[N],sz[N],dep[N],top[N],dfn[N],_index,n,m,fa[N],neg[N],value[N];
void dfs(int start,int from)
{
    int maxn=0;
    sz[start]=1;
    fa[start]=from;
    for(int i=0;i<vec[start].size();i++)
    {
        int end=vec[start][i];
        if(end==from)continue;
        dep[end]=dep[start]+1;
        dfs(end,start);
        sz[start]+=sz[end];
        if(sz[end]>maxn)
        {
            bigson[start]=end;
            maxn=sz[end];
        }
    }
}
void connect(int start,int root)
{
    dfn[start]=++_index;
    top[start]=root;
    neg[dfn[start]]=start;
    if(bigson[start])connect(bigson[start],root);
    for(int i=0;i<vec[start].size();i++)
    {
        int end=vec[start][i];
        if(dep[end]<=dep[start]||bigson[start]==end) continue;
        else connect(end,end);
    }
}
void build(int id,int l,int r,vector<line> lines[],vector<point> pts[],double arr1[],double arr2[])
{
	if(l==r)
	{
		lines[id].push_back(line(-arr1[neg[l]],arr2[neg[l]]));
		return;
	}
	build(lc,l,half,lines,pts,arr1,arr2);
	build(rc,half+1,r,lines,pts,arr1,arr2);
	int p1=0,p2=0;
	vector<line> t;
	while(p1<lines[lc].size()&&p2<lines[rc].size())
	{
		if(lines[lc][p1]>lines[rc][p2]) t.push_back(lines[rc][p2++]);
		else t.push_back(lines[lc][p1++]);
	}
	while(p1<lines[lc].size()) t.push_back(lines[lc][p1++]);
	while(p2<lines[rc].size()) t.push_back(lines[rc][p2++]);
	lines[id].push_back(t[0]);
	int c=0;
	for(int i=1;i<t.size();i++)
	{
		if(t[i].a==lines[id][c].a)
		{
			lines[id][c]=t[i];
			continue;
		}
		if(pts[id].empty())
		{
			add(t[i]);
			continue;
		}
		point a=point(10,t[i].a*10+t[i].b);
		while(!pts[id].empty()&&(a-point(0,t[i].b))*(pts[id][pts[id].size()-1]-point(0,t[i].b))<0) pts[id].pop_back(),lines[id].pop_back();
		c=lines[id].size()-1;
		add(t[i]);
	}
}
double query(int id,int l,int r,int tl,int tr,double mid,vector<line> lines[],vector<point> pts[])
{
	if(l>=tl&&r<=tr)
	{
		int a=lower_bound(pts[id].begin(), pts[id].end(),mid)-pts[id].begin();
		return lines[id][a].a*mid+lines[id][a].b;
	}
	double ans=-1e7;
	if(tl<=half) ans=query(lc,l,half,tl,tr,mid,lines,pts);
	if(tr>half) ans=max(ans,query(rc,half+1,r,tl,tr,mid,lines,pts));
	return ans;
}
double get_path(int st,int ed,double mid,vector<line> lines[],vector<point> pts[])
{
	double ans=-1e7;
	while(top[st]!=top[ed])
	{
		if(dep[top[st]]<dep[top[ed]]) swap(st,ed);
		if(dep[top[st]])
		ans=max(ans,query(1,1,n,dfn[top[st]],dfn[st],mid,lines,pts));
		st=fa[top[st]];
	}
	if(dep[st]<dep[ed]) swap(st,ed);
	if(st) ans=max(ans,query(1,1,n,max(1,dfn[ed]),dfn[st],mid,lines,pts));
	return ans;
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++) scanf("%lf",&x[i]);
	for(int i=1;i<=n;i++) scanf("%lf",&y[i]);
	for(int i=1;i<=n;i++) scanf("%lf",&p[i]);
	for(int i=1;i<=n;i++) scanf("%lf",&q[i]);
	for(int i=1;i<n;i++)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		vec[a].push_back(b);
		vec[b].push_back(a);
	}
	cin>>m;
	dfs(1,0);
	connect(1,1);
	build(1,1,n,lines1,pts1,x,y);
	build(1,1,n,lines2,pts2,p,q);
	for(int i=1;i<=m;i++)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		double l=0,r=100000;
		while(r-l>1e-6)
		{
			double mid=half;
			double t=get_path(a,b,mid,lines1,pts1)+get_path(a,b,mid,lines2,pts2);
			if(t>=0.0) l=mid;
			else r=mid;
		}
		printf("%.4f\n",l);
	}
}