博客作业06--图
1.学习总结(2分)
1.1图的思维导图

1.2 图结构学习体会
图的遍历
- 图的深度优先遍历是从初始点v出发,以纵向的方式逐渐访问各个顶点,一旦找不到相邻的顶点就回退,需要递归的过程,广度遍历是类似层次遍历,利用队列来一一访问
Prim和Kruscal算法
- Prim和Kruscal算法,Prim算法是多次寻找邻边的权重最小值,而Kruskal是需要先对权重排序后查找的,Kruskal在算法效率上是比Prim快的,因为Kruskal只需一次对权重的排序就能找到最小生成树,而Prim算法需要多次对邻边排序才能找到
Dijkstra算法
- Dijkstra算法,在无向图 G=(V,E) 中,假设每条边 E 的长度为 w,找到由顶点 V0 到其余各点的最短路径
- 主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止
拓扑排序
- 拓扑排序:是将一个有向无环图G的所有的顶点排成一个线性序列,使得有向图中的任意的顶点u 和 v 构成的弧,(u, v) 属于该图的边集,并且使得 u 始终是出现在 v 前面
- 只有有向无环图才可以进行拓扑排序
- 算法思想:1.找到有向无环图中没有前驱的节点(或者说是入度为0的节点)输入;2.然后从图中将此节点删除并且删除以该节点为尾的弧
2.PTA实验作业(4分)
2.1 题目1:7-1 图着色问题
2.2 设计思路(伪代码或流程图)
输入顶点数与边数,颜色数进行建图
深度遍历并将其结果储存于数组d中
输入待检查的颜色分配方案的个数num
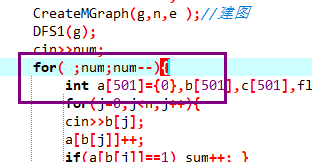
for( ;num;num--){
for j=1 to 顶点数{
输入颜色的分配方案,统计所用颜色总数sum
}
若统计的颜色总数sum!=题干的颜色数
则把flag由0赋为1
}
将颜色按深度遍历排序储存在数组c中
for i=0 to 顶点数{
for j=0 to 顶点数{
若有相邻的颜色相同
则把flag的值由0赋为1
}
flag值已为1即已有相邻颜色相同停止循环
}
如果flag=1 输出no 否则 输出yes
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
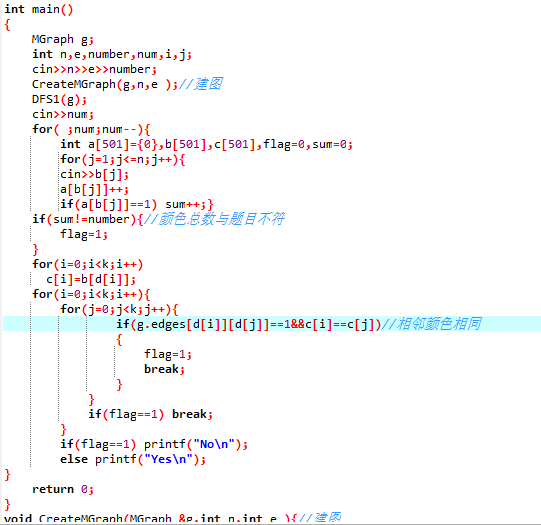
2.4 PTA提交列表说明。
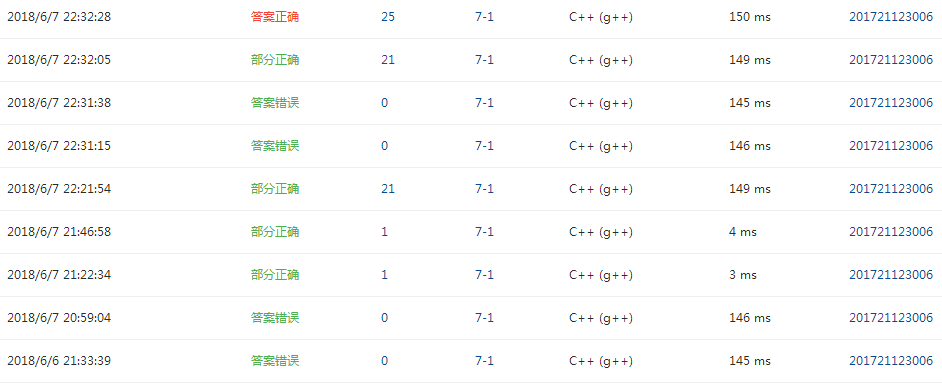
答案错误
部分正确
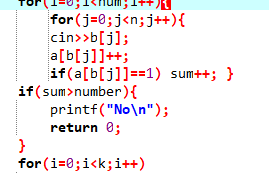
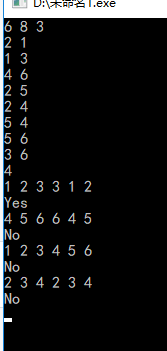

一开始数值赋不进去,只能输出两个,后发现自己在sum这里判断颜色数目时错误直接返回,出错了
改正后输出正常但是输出不对,比样例输出有一个no
自己的循环变量不对,在num循环那里自己忘记循环内有用i,重复使用变量i;
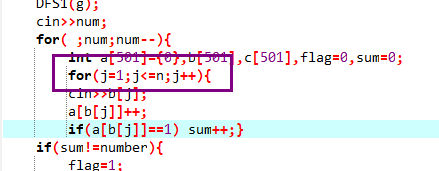
自己的循环条件出错。。。
2.1 题目2:7-3 六度空间
2.2 设计思路(伪代码或流程图)
int bfs(int v)
{
初始化队列
while(队不空)
{
出队元素v
for i=1 to 顶点数
{
若G[v][i]==1 && vis[i]==0
{
count++;
把i进队
tail=i;
}
}
若v为该层最后一个结点
{
层数++
更新层末的顶点
}
若层数为6
跳出循环
}
返回count的值
}
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)

2.4 PTA提交列表说明。


段错误
自己最早用构建邻接矩阵的方式进行赋值,但是赋不进去,总是强制退出,后改为定义二维数组赋值才能很好运行,才正确
2.1 题目3:7-4 公路村村通
2.2 设计思路(伪代码或流程图)
int Prim(int G[MAXV][MAXV],int v)//prim算法计算最短路径
{
定义数组 lowcost[MAXV],closest[MAXV];
lowcost[1]=0;
closest[1]=0;
for i=2 to 顶点数 {
lowcost[i]=G[v][i];
closest[i]=v;
}
for i=2 to 顶点数 {
min置为INFINITY
for j=2 to 顶点数 {
在(V-U)中找出离U最近的顶点k
k记录最近顶点的编号
}
以last更新记录权值长度
lowcost[k]=0;
for j=2 to 顶点数{
若 顶点未被访图联通{
更新
k记录最近顶点
}
}
}
返回last的值
}
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)

2.4 PTA提交列表说明。
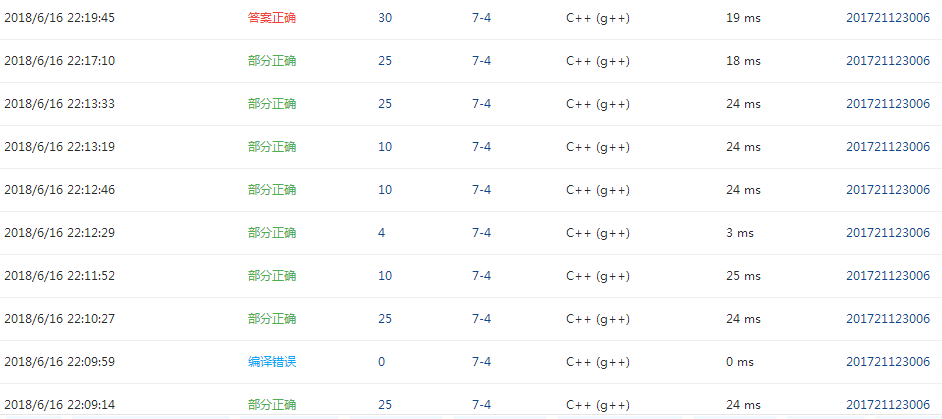

部分正确
自己一开始只有-1的那个点正确

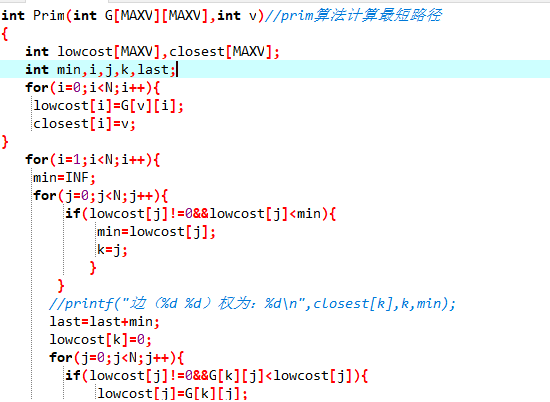
后发现自己的prim算法有问题,是自己的last忘记赋初值
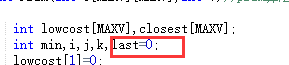

后面的部分正确是自己循环问题,在循环时少了等于,最后一层循环
编译错误
自己的选择c与c++的选择错误
3.截图本周题目集的PTA最后排名(3分)
本次题目集总分:310分
3.1 PTA排名![]()
3.2 我的总分:222
本题评分规则:
(1)PTA总分310分:3分(全部题目都做)
(2)PTA总分在250分--310分:2.5分(大部分做完1)
(3)PTA总分在200--250分:2分(大部分做完2)
(4)PTA总分在150--200分:1.5分
(5)PTA总分在60分-150分:1分
(6)PTA总分在60分以下:0分
4. 阅读代码(必做,1分)
#include<iostream>
using namespace std;
#include<cstring>
#include<cstdio>
#include<queue>
#define inf 0x3f3f3f3f
struct spe
{
int next,to,from;
int len,time;
};
spe edge[250001];
int head[501];
int cnt = 1;
int n,m;
bool cmp( vector<int> a,vector<int> b )
{
if( a.size() != b.size() )
return false;
for( int i= 0 ; i < a.size() ; i++ )
if( a[i] !=b[i] )
return false;
return true;
}
void add(int a,int b,int len,int time)
{
edge[cnt].from = a;
edge[cnt].to = b;
edge[cnt].len = len;
edge[cnt].time = time;
edge[cnt].next = head[a];
head[a] = cnt;
cnt++;
}
struct node_num
{
int prev,num;
};
node_num node[501];
struct node_time
{
int prev,len;
};
node_time nod[501];
int spfa_time( int start, int end )
{
queue<int> q;
int visit[501];
int dis[501];
memset(visit,0,sizeof(visit));
memset(dis,0,sizeof(dis));
memset(nod,0,sizeof(nod));
for( int i = 0 ; i < n ; i++ )
nod[i].len = inf;
nod[0].prev = inf;
nod[start].prev = start;
nod[start].len = 0;
for( int i = 0 ; i < n ; i++ )
dis[i] = inf;
q.push(start);
dis[start] = 0;
visit[start] = 1;
while( !q.empty() )
{
int t = q.front(); q.pop();
for( int i = head[t] ; i != -1 ; i = edge[i].next )
{
if( dis[t] + edge[i].time < dis[ edge[i].to ] )
{
dis[ edge[i].to ] = dis[t] + edge[i].time;
nod[ edge[i].to ].prev = t;
nod[ edge[i].to ].len = nod[t].len+edge[i].len;
if( visit[edge[i].to] == 0 )
{
visit[edge[i].to] = 1;
q.push(edge[i].to);
}
}
else if( dis[t] + edge[i].time == dis[ edge[i].to ] )
{
if( nod[t].len + edge[i].len < nod[ edge[i].to ].len )
{
nod[ edge[i].to ].len = nod[t].len + nod[ edge[i].to ].len;
nod[ edge[i].to ].prev = t;
}
}
}
}
return dis[end];
}
int spfa_len( int start, int end )
{
queue<int> q;
int visit[501];
int dis[501];
memset(visit,0,sizeof(visit));
memset(dis,0,sizeof(dis));
memset(node,0,sizeof(node));
for( int i = 0 ; i < n ; i++ )
node[i].num = inf;
node[0].prev = inf;
node[start].prev = start;
node[start].num = 0;
for( int i = 0 ; i < n ; i++ )
dis[i] = inf;
q.push(start);
dis[start] = 0;
visit[start] = 1;
while( !q.empty() )
{
int t = q.front(); q.pop();
for( int i = head[t] ; i != -1 ; i = edge[i].next )
{
if( dis[t] + edge[i].len < dis[ edge[i].to ] )
{
dis[ edge[i].to ] = dis[t] + edge[i].len;
node[ edge[i].to ].prev = t;
node[ edge[i].to ].num = node[t].num+1;
if( visit[edge[i].to] == 0 )
{
visit[edge[i].to] = 1;
q.push(edge[i].to);
}
}
else if( dis[t] + edge[i].len == dis[ edge[i].to ] )
{
if( node[t].num + 1 < node[ edge[i].to ].num )
{
node[ edge[i].to ].num = node[t].num + 1;
node[ edge[i].to ].prev = t;
}
}
}
}
return dis[end];
// cout<<"LEN:"<<dis[end]<<endl;
}
int main()
{
while( scanf("%d %d",&n,&m) == 2 )
{
memset(head,-1,sizeof(head));
for( int i = 1 ; i <= m ; i++ )
{
int a,b,c,d,e;
scanf("%d %d %d %d %d",&a,&b,&c,&d,&e);
add(a,b,d,e);
if( c == 0 )
add(b,a,d,e);
}
int start,end;
scanf("%d %d",&start,&end);
int LEN = spfa_len(start,end);
int TIME = spfa_time(start,end); //两个spfa
vector<int> len,time;
int t = end;
while( node[t].prev != t )
{
len.push_back(t);
t = node[t].prev;
}
len.push_back(start); //prev数组顺序是反的
t = end;
while( nod[t].prev != t )
{
time.push_back(t);
t = nod[t].prev;
}
time.push_back(start);
if( cmp(len,time) )
{
printf("Time = %d; Distance = %d:",TIME,LEN);
for( int i = time.size() - 1 ; i >= 0 ; i-- )
{
if( i )
printf(" %d =>",time[i]);
else printf(" %d\n",time[i]);
}
}
else
{
printf("Time = %d:",TIME);
for( int i = time.size() - 1 ; i >= 0 ; i-- )
{
if( i )
printf(" %d =>",time[i]);
else printf(" %d\n",time[i]);
}
printf("Distance = %d:",LEN);
for( int i = len.size() - 1 ; i >= 0 ; i-- )
{
if( i )
printf(" %d =>",len[i]);
else printf(" %d\n",len[i]);
}
}
}
return 0;
}





 浙公网安备 33010602011771号
浙公网安备 33010602011771号