矩阵快速幂和普通快速幂类似,只是数据结构变成了矩阵
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int mod=1000000007;
struct matrix{
LL c[101][101];
matrix(){memset(c, 0, sizeof c);}
} A, res;
LL n, k;
matrix operator*(matrix &x, matrix &y){ //矩阵乘法
matrix t; //临时矩阵
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
for(int k=1; k<=n; k++)
t.c[i][j]=(t.c[i][j]+x.c[i][k]*y.c[k][j])%mod;
return t;
}
void quickpow(LL k){ //快速幂
for(int i=1; i<=n; i++) res.c[i][i]=1; //单位矩阵
while(k){
if(k & 1) res = res*A;
A = A*A;
k >>= 1;
}
}
int main(){
scanf("%d%lld",&n,&k);
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
scanf("%d",&A.c[i][j]);
quickpow(k);
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++)
printf("%d ",res.c[i][j]);
puts("");
}
return 0;
}
递推优化:
看所求元素是否能表示成一项乘以一个矩阵等于下一项
比如求斐波那契数列Fn=Fn-1+Fn-2
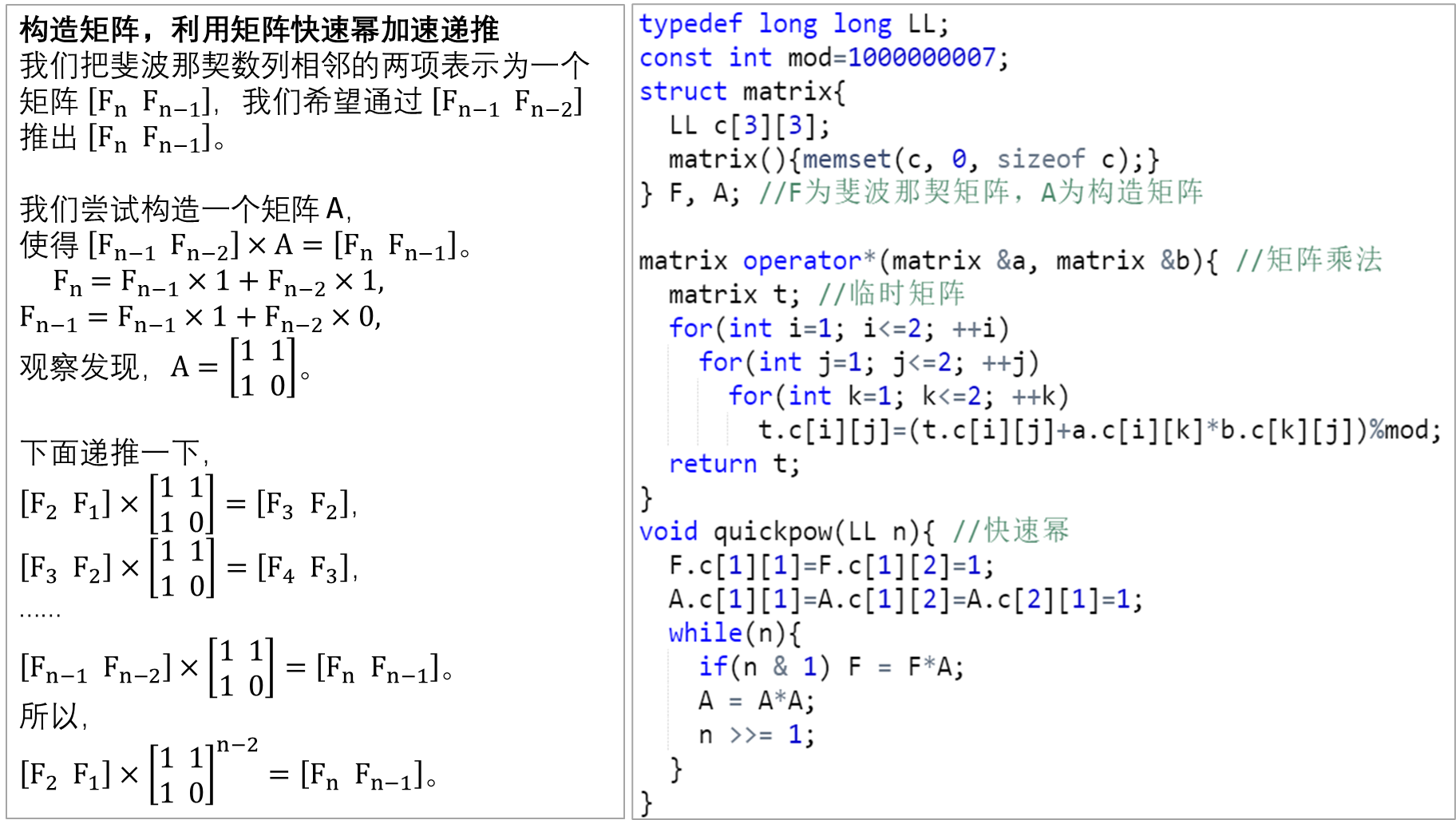
// O(2^3*logn)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int mod=1000000007;
struct mat{
LL c[2][2];
mat(){memset(c,0,sizeof c);}
}F,A; //F:数列矩阵 A:转移矩阵
mat operator*(const mat &a,const mat &b){
mat t;
for(int i=0; i<2; ++i)
for(int j=0; j<2; ++j)
for(int k=0; k<2; ++k)
t.c[i][j]=(t.c[i][j]+a.c[i][k]*b.c[k][j])%mod;
return t;
}
void qpow(LL n){
F.c[0][0]=F.c[0][1]=1;
A.c[0][0]=A.c[0][1]=A.c[1][0]=1;
while(n){
if(n&1) F=F*A;
A=A*A;
n>>=1;
}
}
int main(){
LL n; cin>>n;
if(n<=2){puts("1"); return 0;}
qpow(n-2);
cout<<F.c[0][0];
}


