深度-广度搜索-状态空间

-
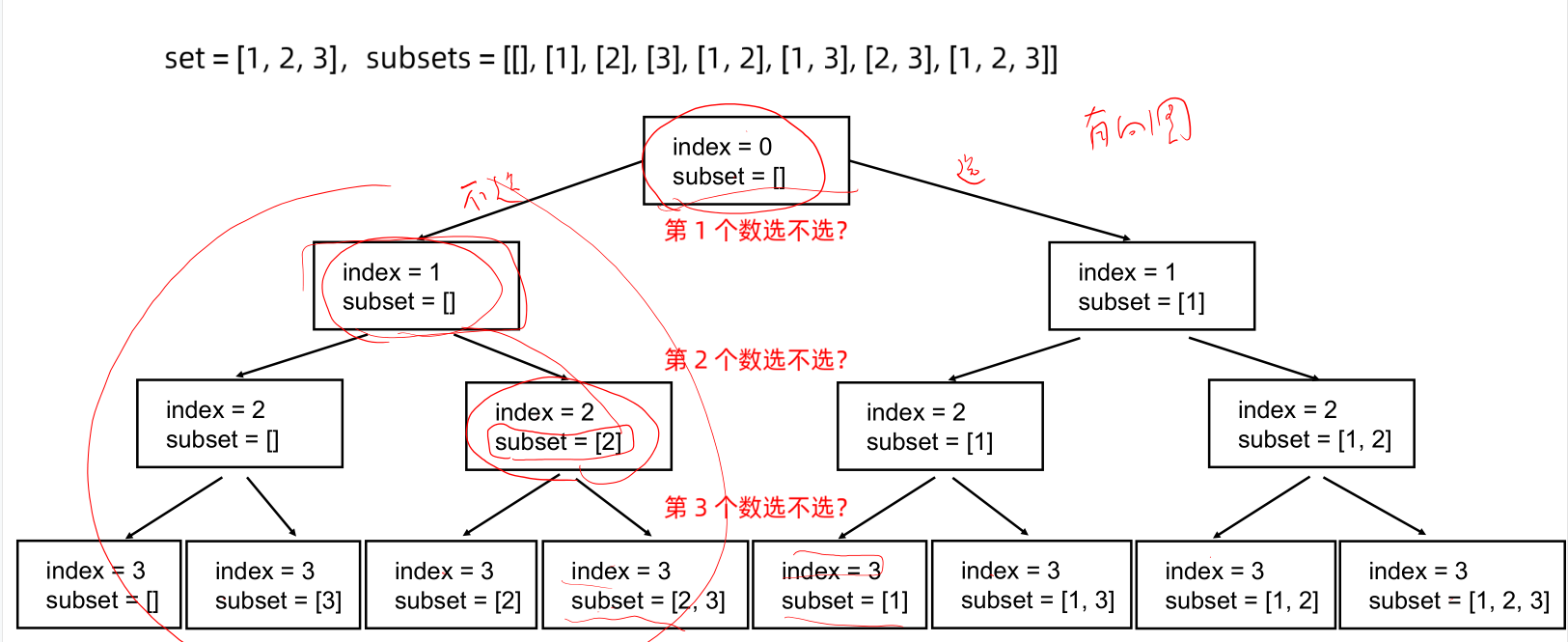
求子集
-
上图把问题抽象成为图的遍历
17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
示例 2:
输入:digits = ""
输出:[]
示例 3:
输入:digits = "2"
输出:["a","b","c"]
提示:
0 <= digits.length <= 4digits[i]是范围['2', '9']的一个数字。
解题思路
1. 问题抽象为状态空间
2. 遍历所有可能的状态空间
完整代码
/**
* @param {string} digits
* @return {string[]}
*/
var letterCombinations = function(digits) {
// 我们使用搜索算法
// 把问题抽象成状态空间
// 变化的状态 index s(结果字符串)
// 维护数字到字母字符串的映射
let edges={
'2':['a','b','c'],
'3':['d','e','f'],
'4':['g','h','i'],
'5':['j','k','l'],
'6':['m','n','o'],
'7':['p','q','r','s'],
'8':['t','u','v'],
'9':['w','x','y','z']
}
let s=''
let res=[]
// 遍历状态空间
const dfs=(s,index)=>{
// 到达深搜终点,返回
if(s.length===digits.length){
if(s.length===0) return
res.push(s)
return
}
// 出边数组,即下一步可能的出边
// console.log(edges[digits[0]])
let arr=edges[digits[index]]
// 走向不同的状态空间
arr.forEach((item)=>{
dfs(s+item,index+1)
})
}
dfs(s,0)
return res
};
51. N 皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:

输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
提示:
-
1 <= n <= 9 -
判断对角线的方法

解题思路
1. 全排列的状态空间
2. 在全排列的基础上排除有对角线的
完整代码
/**
* @param {number} n
* @return {string[][]}
*/
var solveNQueens = function(n) {
// 先计算出全排列
let res=[]
// 定义对角线是否使用对象
let useIplusJ={}
let useIminsJ={}
const dfs=(arr)=>{
let depth=arr.length
if(arr.length===n){
res.push(Array.from(arr))
}
for(let i=0;i<n;i++){
if(!arr.includes(i)&&!useIplusJ[depth+i]&&!useIminsJ[depth-i]){
// 我们在加上对角线的限制
useIplusJ[depth+i]=true
useIminsJ[depth-i]=true
dfs(arr.concat(i))
useIplusJ[depth+i]=false
useIminsJ[depth-i]=false
}
}
}
dfs([])
console.log(res)
const newRes=res.map(item=>{
return item.map(ele=>{
let s=''
for(let i=0;i<n;i++){
if(i===ele){
s+='Q'
}else{
s+='.'
}
}
return s
})
})
return newRes
};
200. 岛屿数量(地图dfs模板题)
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]的值为'0'或'1'
解题思路
1. 需要理解题意
2. 找岛屿个数,其实是找所有相互连接(相邻)的1的集群
3. 集群的个数即为岛屿的个数
地图dfs
/**
* @param {character[][]} grid
* @return {number}
*/
var numIslands = function(grid) {
// 即寻找1的所有连通图
let res=0
// 行
let m=grid.length
// 列
let n=grid[0].length
// 访问数组
let visited=new Array(m)
for(let i=0;i<m;i++){
let arr=new Array(n).fill(false)
visited[i]=arr
}
// 定义一个方向数组
let dx=[-1,0,1,0]
let dy=[0,1,0,-1]
const dfs=(x,y)=>{
visited[x][y]=true
// 寻找当前节点的所有出边,即相邻的方向
for(let i=0;i<4;i++){
// 4个方向
let nx=x+dx[i]
let ny=y+dy[i]
if(nx<0||ny<0||nx>=m||ny>=n) continue
// 合法
if(grid[nx][ny]==='1'&&!visited[nx][ny]){
dfs(nx,ny)
}
}
}
// 寻找连通图的个数
for(let i=0;i<m;i++){
for(let j=0;j<n;j++){
if(grid[i][j]==='1'&&!visited[i][j]){
dfs(i,j)
res++
}
}
}
return res
};
地图bfs
/**
* @param {character[][]} grid
* @return {number}
*/
var numIslands = function(grid) {
// 广度优先搜索
// 找有几个连通图
let res=0
let m=grid.length
let n=grid[0].length
// 方向数组
let dx=[-1,0,1,0]
let dy=[0,1,0,-1]
// 定义一个visited数组,记录是否被访问
let visited=new Array(m)
for(let i=0;i<m;i++){
let arr=new Array(n).fill(false)
visited[i]=arr
}
// console.log(visited)
const bfs=(x,y)=>{
// 广度优先搜索,维护一个队列
let queue=[]
queue.push([x,y])
visited[x][y]=true
while(queue.length){
let first=queue[0][0]
let second=queue[0][1]
queue.shift()
// 遍历所有的出边
for(let i=0;i<4;i++){
let nx=first+dx[i]
let ny=second+dy[i]
if(nx<0||ny<0||nx>=m||ny>=n) continue
if(grid[nx][ny]==='1'&&!visited[nx][ny]){
queue.push([nx,ny])
console.log('nx',nx,'ny',ny)
visited[nx][ny]=true
}
}
}
}
// 开始遍历没有访问过的1
for(let i=0;i<m;i++){
for(let j=0;j<n;j++){
if(grid[i][j]==='1'&&!visited[i][j]){
// console.log(i,j)
bfs(i,j)
// console.log(visited)
res++
}
}
}
return res
};
130. 被围绕的区域
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例 1:

输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例 2:
输入:board = [["X"]]
输出:[["X"]]
提示:
m == board.lengthn == board[i].length1 <= m, n <= 200board[i][j]为'X'或'O'
解题思路
1. 还是找连通图
2. 不过加上了限制条件,不能选取连接在边缘的连通图
完整代码
/**
* @param {character[][]} board
* @return {void} Do not return anything, modify board in-place instead.
*/
var solve = function(board) {
let m=board.length
let n=board[0].length
let visited=new Array(m)
for(let i=0;i<m;i++){
let arr=new Array(n).fill(false)
visited[i]=arr
}
// 存放需要修改的下标数组
let res=[]
// 连通图访问,如果判断为封闭,push到res
let temp=[]
// 判断区域是否被环绕
var has=false
let dx=[-1,0,1,0]
let dy=[0,1,0,-1]
const dfs=(x,y)=>{
temp.push([x,y])
visited[x][y]=true
for(let i=0;i<4;i++){
nx=x+dx[i]
ny=y+dy[i]
// 合法性判断
if(nx<0||ny<0||nx>=m||ny>=n){
continue
}
// O走到了边缘,不是被环绕
if((nx===0||ny===0||nx===m-1||ny===n-1)){
// console.log('nx',nx,'ny',ny)
if(!visited[nx][ny]&&board[nx][ny]==='O')
has=true
// break
}
// 不是边缘,继续走
if(board[nx][ny]==='O'&&!visited[nx][ny]){
dfs(nx,ny)
}
}
// visited[x][y]=false
}
// 我们从零开始遍历联通
for(let i=0;i<m;i++){
for(let j=0;j<n;j++){
// 边缘我们不考虑
if(i==0||j===0||i===m-1||j===n-1) continue
if(board[i][j]==='O'&&!visited[i][j]){
has=false
// 存放走过的O,可能是正确解
temp=[]
dfs(i,j)
// 确实被环绕
if(!has){
res.push(Array.from(temp))
}
}
}
}
console.log(res)
// 将被环绕的点修改为X
res.forEach(item=>{
item.forEach(item2=>{
board[item2[0]][item2[1]]='X'
})
})
// return []
};
433. 最小基因变化
基因序列可以表示为一条由 8 个字符组成的字符串,其中每个字符都是 'A'、'C'、'G' 和 'T' 之一。
假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。
- 例如,
"AACCGGTT" --> "AACCGGTA"就是一次基因变化。
另有一个基因库 bank 记录了所有有效的基因变化,只有基因库中的基因才是有效的基因序列。(变化后的基因必须位于基因库 bank 中)
给你两个基因序列 start 和 end ,以及一个基因库 bank ,请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化,返回 -1 。
注意:起始基因序列 start 默认是有效的,但是它并不一定会出现在基因库中。
示例 1:
输入:start = "AACCGGTT", end = "AACCGGTA", bank = ["AACCGGTA"]
输出:1
示例 2:
输入:start = "AACCGGTT", end = "AAACGGTA", bank = ["AACCGGTA","AACCGCTA","AAACGGTA"]
输出:2
示例 3:
输入:start = "AAAAACCC", end = "AACCCCCC", bank = ["AAAACCCC","AAACCCCC","AACCCCCC"]
输出:3
提示:
start.length == 8end.length == 80 <= bank.length <= 10bank[i].length == 8start、end和bank[i]仅由字符['A', 'C', 'G', 'T']组成
解题思路
1. 写出状态空间,根据状态空间搜索
2. 因为题目是看变化最小次数达到目的,适合实验bfs搜索
3. 搜索的层数即为变化的次数
完整代码
/**
* @param {string} start
* @param {string} end
* @param {string[]} bank
* @return {number}
*/
var minMutation = function(start, end, bank) {
// 解题思路
// 画出所有的状态空间
// 基因长度为8
// 总的基于序列个数 4^8
// 对于每个基因,变化1次,出边 3*8
// 则规模 4^8 *24
// 广度优先搜索
// 在第n层搜到,说明变化次数即为n次
let queue=[]
// 存储每个节点对应的深度
let depth={}
let gens=['A','C','G','T']
// 广度,维护一个队列
queue.push(start)
depth[start]=0
while(queue.length){
let str=queue.shift()
// 开始变化,变化一次
for(let i=0;i<8;i++){
for(let j=0;j<4;j++){
if(str.charAt(i)!==gens[j]){
// 变化成新的字符串
let newStr=''
for(let m=0;m<8;m++){
if(m===i){
newStr+=gens[j]
}else{
newStr+=str[m]
}
}
// 判断新的字符串是否合法
if(bank.includes(newStr)){
// 产生的新基因没有访问过
if(!depth[newStr]){
// console.log(newStr)
depth[newStr]=depth[str]+1
queue.push(newStr)
if(newStr===end){
return depth[newStr]
}
}
}
}
}
}
}
return -1
};
329. 矩阵中的最长递增路径
给定一个 m x n 整数矩阵 matrix ,找出其中 最长递增路径 的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外(即不允许环绕)。
示例 1:

输入:matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
示例 2:

输入:matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
示例 3:
输入:matrix = [[1]]
输出:1
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 2000 <= matrix[i][j] <= 231 - 1
解题思路
1. dfs 暴力,遍历每个节点能走的深度,取出最大值,超时
2. dfs+记忆数组
遍历每个节点能走的深度,同时记录这个深度,这样其他
节点获取深度时,可以根据已经记录的深度,减少计算量
dfs+记忆化 完整代码
/**
* @param {number[][]} matrix
* @return {number}
*/
var longestIncreasingPath = function(matrix) {
// 使用普通的dfs会超时
// dfs+记忆化
// 我们记忆每个格子往高处走,能走多远
// 其实不需要visited数组,为什么
// 因为只能往高处走,不会形成环
let m=matrix.length
let n=matrix[0].length
// 使用dfs
// let visited=new Array(m)
// 记录每个格子能走多远
let howFar=new Array(m)
for(let i=0;i<m;i++){
// let arr=new Array(n).fill(false)
let arr1=new Array(n).fill(1)
// visited[i]=arr
howFar[i]=arr1
}
let dx=[-1,0,1,0]
let dy=[0,1,0,-1]
let res=-1
const dfs=(x,y)=>{
if(howFar[x][y]!==1) return howFar[x][y]
// 开始遍历所有的出边
for(let i=0;i<4;i++){
let nx=x+dx[i]
let ny=y+dy[i]
if(nx<0||ny<0||nx>=m||ny>=n) continue
if(matrix[nx][ny]>matrix[x][y]){
howFar[x][y]=Math.max(howFar[x][y],dfs(nx,ny)+1)
}
}
return howFar[x][y]
}
for(let i=0;i<m;i++){
for(let j=0;j<n;j++){
res=Math.max(res,dfs(i,j))
}
}
return res
};
bfs
/**
* @param {number[][]} matrix
* @return {number}
*/
var longestIncreasingPath = function (matrix) {
// bfs进行拓扑排序
// 我们遍历节点从入度为0的开始
// 遍历它的出边数组时,把出边对应的入度-1
let m = matrix.length;
let n = matrix[0].length;
let dx = [-1, 0, 1, 0];
let dy = [0, 1, 0, -1];
// 这里deg数组使用了二维数组,其实可以使用一维数组(降维,压缩)
let inDeg = new Array(m * n).fill(0);
// 出边数组,如果直接存储,数组为变成三维,比较难维护,我们降维
let edges = [];
// 距离数组,记录每个节点能走的最大值,默认是1
let dist = new Array(m * n).fill(1);
for (let i = 0; i < m * n; i++) {
let arr = Array.from([]);
edges.push(arr);
}
// 遍历所有节点,存储入度数组
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
for (let k = 0; k < 4; k++) {
let nx = i + dx[k];
let ny = j + dy[k];
if (nx < 0 || ny < 0 || nx >= m || ny >= n) {
continue;
}
if (matrix[nx][ny] < matrix[i][j]) {
inDeg[i * n + j]++;
}
if (matrix[i][j] < matrix[nx][ny]) {
edges[i * n + j].push(nx * n + ny);
}
}
}
}
// console.log(inDeg);
// console.log(edges);
const tpSort = () => {
// 开始拓扑排序
let queue = [];
for (let i = 0; i < m * n; i++) {
// 入度为0
if (inDeg[i] === 0) {
queue.push(i);
}
// queue.push(x)
}
while (queue.length) {
let m = queue[0];
queue.shift();
// 它的出边(入度为0的)入队
edges[m].forEach((item) => {
inDeg[item]--;
dist[item] = Math.max(dist[item], dist[m] + 1);
if (inDeg[item] === 0) {
queue.push(item);
}
});
}
};
tpSort()
// console.log(dist);
let res=0
for(let i=0;i<dist.length;i++){
res=Math.max(res,dist[i])
}
return res
};






 浙公网安备 33010602011771号
浙公网安备 33010602011771号