树与图

589. N 叉树的前序遍历

给定一个 n 叉树的根节点 root ，返回其节点值的 前序遍历 。

n 叉树在输入中按层序遍历进行序列化表示，每组子节点由空值 null 分隔（请参见示例）。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：[1,3,5,6,2,4]

示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[1,2,3,6,7,11,14,4,8,12,5,9,13,10]

提示：

节点总数在范围 [0, 104]内
0 <= Node.val <= 104
n 叉树的高度小于或等于 1000

解题思路

1. 变量，前序==>深度优先搜索
2. n叉树=>遍历根，遍历所有孩子节点

递归

 const preOrder=(root)=>{
         if(!root){
             return 
         }
    
         // console.log(root.val)
         res.push(root.val)

         // console.log(root.children)
         for(let i=0;i<root.children.length;i++){
            preOrder(root.children[i])
         }
     }

迭代

关键在于使用栈来模拟递归的堆栈调用

/**
 * // Definition for a Node.
 * function Node(val, children) {
 *    this.val = val;
 *    this.children = children;
 * };
 */

/**
 * @param {Node|null} root
 * @return {number[]}
 */
var preorder = function(root) {

    // 迭代的方法实现

    // 关键在于使用栈来模拟递归调用堆栈

    // const preOrder=(root)=>{
    //     if(!root){
    //         return 
    //     }
    
    //     // console.log(root.val)
    //     res.push(root.val)

    //     // console.log(root.children)
    //     for(let i=0;i<root.children.length;i++){
    //         preOrder(root.children[i])
    //     }
    // }

    let res=[]

    let stack=[]

    stack.push(root)
    
    while(stack.length){
        
        let node=stack.pop()
        if(!node) break
        res.push(node.val)
        for(let i=node.children.length-1;i>=0;i--){
            stack.push(node.children[i])
        }
    }
    


    return res
    
};

429. N 叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]

示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

提示：

树的高度不会超过 1000
树的节点总数在 [0, 10^4] 之间

解题思路

1. 层序遍历，一般需要使用队列维护
2. 结果集分组，需要为队列中的每个元素添加深度

完整代码

/**
 * // Definition for a Node.
 * function Node(val,children) {
 *    this.val = val;
 *    this.children = children;
 * };
 */

/**
 * @param {Node|null} root
 * @return {number[][]}
 */

 function NodeWithLevel(node,level){

     this.node=node
     this.level=level

 }
var levelOrder = function(root) {

    let res=[]
    
    // 层序遍历，一般都是使用一个队列来维护
    let queue=[]

    let levelNode=new NodeWithLevel(root,1)
    queue.push(levelNode)

    while(queue.length){

        let levelNode=queue.shift()
        
        if(!levelNode.node) break

        // 结果集合
        let level=levelNode.level-1
        // res[level]=res[level]===undefined? []:res[level].push(levelNode.node.val) 

        if(res[level]){
            res[level].push(levelNode.node.val)
        }else{
            res[level]=new Array()
            res[level].push(levelNode.node.val)
        }

        // 孩子节点入队
        
        let length=levelNode.node.children.length

        for(let i=0;i<length;i++){
            let aNode=new NodeWithLevel(levelNode.node.children[i],levelNode.level+1)
            queue.push(aNode)
        }
    }


    return res


};

297. 二叉树的序列化与反序列化

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

示例 1：

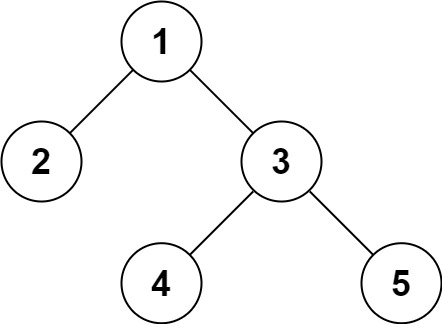
输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[1,2]

提示：

树中结点数在范围 [0, 104] 内
-1000 <= Node.val <= 1000

解题思路

1. 序列化和反序列化其实就是树结构和字符串的转化
2. 序列化将树结构转化为前序字符串
3. 反序列化将前序字符串转化为树结构

完整代码

/**
 * // Definition for a Node.
 * function Node(val,children) {
 *    this.val = val;
 *    this.children = children;
 * };
 */

/**
 * @param {Node|null} root
 * @return {number[][]}
 */

 function NodeWithLevel(node,level){

     this.node=node
     this.level=level

 }
var levelOrder = function(root) {

    let res=[]
    
    // 层序遍历，一般都是使用一个队列来维护
    let queue=[]

    let levelNode=new NodeWithLevel(root,1)
    queue.push(levelNode)

    while(queue.length){

        let levelNode=queue.shift()
        
        if(!levelNode.node) break

        // 结果集合
        let level=levelNode.level-1
        // res[level]=res[level]===undefined? []:res[level].push(levelNode.node.val) 

        if(res[level]){
            res[level].push(levelNode.node.val)
        }else{
            res[level]=new Array()
            res[level].push(levelNode.node.val)
        }

        // 孩子节点入队
        
        let length=levelNode.node.children.length

        for(let i=0;i<length;i++){
            let aNode=new NodeWithLevel(levelNode.node.children[i],levelNode.level+1)
            queue.push(aNode)
        }
    }


    return res


};

105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

解题思路

1. 前序序列告诉我们根的值
2. 中序遍历告诉我们根的位置
3. 降规模
	原树划分为左子树和右子树
	重复1，2操作
	
4. 递归出口，前序序列的范围不合法

完整代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {

    // 我们把问题进行分解降规模

    // 对于[3,9,20,15,7]
    // 前序遍历告诉我们root=3
    // 中序遍历[9,3,15,20,7] 告诉我们3的位置

    // 问题分解为

    [9 | 3 | 15,20,7]

    // 左子树[9]
    // 右子树 [15,20,7]

    // 对左右子树递归分解问题

    

    // 递归子问题
    const build=(l1,r1,l2,r2)=>{

        // l1 r1 确定前序序列的范围

        // l2,r2 确定中序序列的范围

        if(l1>r1){
            return null
        }

        // 确定根
        let root =new TreeNode(preorder[l1])

        

        // 确定分界点
        // 从中序序列找，找到根
        let point=l2
        while(inorder[point]!==preorder[l1]){
            point++
        }

        // 确定左子树和右子树

        let leftSize=point-l2
        // let rightSize=r2-point



        root.left=build(l1+1,l1+leftSize,l2,point-1)
        root.right=build(l1+leftSize+1,r1,point+1,r2)

        return root
    }

    return build(0,preorder.length-1,0,inorder.length-1)


};

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。

解题思路

1. 暴力
	把每个节点遍历一次，同时存储每个节点的父节点和深度
	遍历过程找到p,q节点
	根据找出的 p,q 节点通过存储的父节点找到祖先

优化版本

1. 思路还是暴力，但在空间和时间复杂度上有优化
	我们只存储每个节点的父节点和一个激化标记（默认false）
	q节点往上走到根，走过的激化(包含自身)标记为true
	p节点往上走，遇到激活标记结束，找到了共同祖先
	
	
	其实空间复杂度差不多，时间上有优化，不需要每次比较值，只需要看激活标记即可

心得体会

1. 把原节点变为包含额外父节点的节点 ，可以定义一个数据结构，将原数据结构node进行改造，但是空间有浪费

2. 其实应该这样 function MyNode(val,node){
	this.val=val
	this.parentNode=node
}

3. 或者使用map

let m=new Map()
m.set(p.val,p.parentNode)

完整代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */

 function MyNode(node,parentNode,depth){

     this.node=node
     this.parentNode=parentNode
     this.depth=depth
 }
var lowestCommonAncestor = function(root, p, q) {

    // 1.  暴力
    
    // 将这棵树遍历一次，每个节点存储它的父节点和该节点对应的层数

    // 这里使用广度优先遍历

    let queue=[]

    let myNodeList=[]

    let myRoot=new MyNode(root,null,0)


    queue.push(myRoot)
    myNodeList.push(myRoot)

    let pNode;
    let qNode;

    while(queue.length){

        let curNode=queue.shift()
        if(!curNode.node) break

        // console.log(curNode.node.val)

        if(curNode.node.val===p.val){
            console.log(1)
            pNode=curNode
        }

        if(curNode.node.val===q.val){
            qNode=curNode
        }

        let leftNode=curNode.node.left
        let rightNode=curNode.node.right

        if(leftNode){
            let myLeftNode=new MyNode(leftNode,curNode,curNode.depth+1)
            queue.push(myLeftNode)
        }

        if(rightNode){
            let myRightNode=new MyNode(rightNode,curNode,curNode.depth+1)
            queue.push(myRightNode)
        }
    }

    console.log(pNode)
    console.log(qNode)

    // 开始寻找祖先

    // 我们先让p，q节点层级相同

    while(pNode.depth>qNode.depth){
        pNode=pNode.parentNode
    }

    while(qNode.depth>pNode.depth){
        qNode=qNode.parentNode
    }

    const getParent=(pNode,qNode)=>{
        // 层数相同
        if(pNode.depth===qNode.depth){
            // 一路往上找父节点
            let p=pNode
            let q=qNode

            while(p.node.val!==q.node.val){
                p=p.parentNode
                q=q.parentNode
            }

            // console.log(p)

            return p
        }
    }

    const res=getParent(pNode,qNode)

    console.log(res)

    return res.node
};

优化版本

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function(root, p, q) {
    
    // 使用map简化空间复杂度
    let map=new Map()

    // 使用标记数组存储节点 优化时间复杂度
    let redNodes=new Set()

    // 遍历树
    map.set(root.val,null)
    const travelTree=(root)=>{
        if(!root){
            return 
        }

        if(root.left){
            map.set(root.left.val,root)
            travelTree(root.left)
        }

        if(root.right){
            map.set(root.right.val,root)
            travelTree(root.right)
        }
    }

    travelTree(root)

    // p 往上走，走到根，其中经过的节点全部加入redNodes数组

    while(p.val!==root.val){
        redNodes.add(p.val)
        p=map.get(p.val)
    }

    while(q.val!==root.val){
        if(redNodes.has(q.val)){
            break
        }
        q=map.get(q.val)
    }

    return q
};

684. 冗余连接(模板题)（用于找环的模板）

树可以看成是一个连通且无环的无向图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

示例 1：

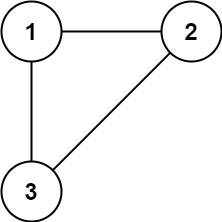
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

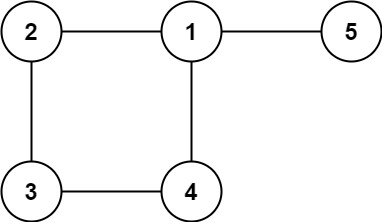
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

提示:

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

无向图找环

解题思路

1. 这条玩文字游戏，其实本质就是判断每加入一条边是否可以形成环
2. 如果形成了，把新加的边返回
3. 如何判断是否有环
	1. 双向图
	2. 递归出边
	3. 递归的出边可以是父亲，也可以是其他边
		递归父亲不算，如果其他边已经被访问过了，说明形成了环

完整代码

/**
 * @param {number[][]} edges
 * @return {number[]}
 */
var findRedundantConnection = function (edges) {
  // 问题的本质在于找环

  // dfs找环

  // 我们一条边一条边的加，看没加一条边是否会形成环，如果形成，则返回

  // 定义一个出边数组
  let arr = new Array(edges.length)
  for (let i = 0; i < edges.length + 1; i++) {
    // let newArr=new Array()
    arr[i] = []
  }

  // dfs找环
  // 定义一个visited数组
  let visited = new Array(edges.length + 1).fill(false)
  let hasCycle = false

  const dfs = (x, father) => {
    visited[x] = true
    // 遍历出边，因为双向，所以可以出边指向父亲，执行父亲的不算
    arr[x].forEach((item) => {
      if (item === father) return

      if (visited[item]) {
        hasCycle = true
      } else {
        dfs(item, x)
      }
    })
  }

  // 遍历edges数组，双向加边
  for (let i = 0; i < edges.length; i++) {
    let source = edges[i][0]
    let target = edges[i][1]

    arr[source].push(target)
    arr[target].push(source)

    // 每加一条边，看是否存在环,父亲一开始没有(-1)
    for (let i = 0; i < edges.length + 1; i++) {
      visited[i] = false
    }
    dfs(source, -1)
    if (hasCycle) return edges[i]
  }

  return null
}

207. 课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

1 <= numCourses <= 105
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对 互不相同

解题方法

dfs有向图找环
bfs有向图找环

dfs

1. 深度搜索，遇到没有访问过的节点就递归调用
2. 一路递归下去，在没有返回的情况下，如果发现某个节点的出边已经被访问，有环
3. 递归回头时，把该节点已经访问设为false（防止假环）

/**
 * @param {number} numCourses
 * @param {number[][]} prerequisites
 * @return {boolean}
 */
var canFinish = function(numCourses, prerequisites) {

    // 课程表，判断能否修完所有课程的标准为
    // 不形成环 ==>可以
    // 形成环==> 不可以

    // 深度优先搜索看是否形成了环

   

    // 定义出边数组
    let arr=new Array(numCourses)

    for(let i=0;i<numCourses;i++){
        arr[i]=[]
    }

    // 根据课程表加边
    let hasCycle=false
    let visited=new Array(numCourses).fill(false)

     const dfs=(x)=>{
        visited[x]=true
        // x的出边
        for(let i=0;i<arr[x].length;i++){
            if(visited[arr[x][i]]){
                hasCycle=true
                break
            } else{
                dfs(arr[x][i])
            }
        }
        visited[x]=false
    }
    for(let i=0;i<prerequisites.length;i++){

        let target=prerequisites[i][0]
        let source=prerequisites[i][1]

        for(let j=0;j<visited.length;j++){
            visited[j]=false
        }

        arr[source].push(target)

        console.log(source)

        dfs(source)

        // 判断是否形成环
        if(hasCycle){
            return false
        }
    }

    return true

};

bfs 找环法

有向图的一些概念

出度：该节点指向其他节点的边的数量
入度：其他节点指向该节点的边的数量

1. 找环方法
	找到入度为0的节点，访问
	它可能指向了其他节点，被指向的节点入度-1
	
	循环上述操作，如果所有节点都被访问了，说明没有环
	否则有环

/**
 * @param {number} numCourses
 * @param {number[][]} prerequisites
 * @return {boolean}
 */
var canFinish = function(numCourses, prerequisites) {

    // 使用bfs找环

    // 判断入度为0的点开始学习

    // 直到没有入度为0的节点，这时候看看已经访问过的节点是否等于课程数

    // 定义出边数组
    let arr=new Array(numCourses)

    // 定义入度数组，记录每个节点的入度
    let inDeg=new Array(numCourses).fill(0)

    for(let i=0;i<numCourses;i++){
        arr[i]=[]
    }

    const tpSort=()=>{

        // 找到入度为0的节点

        let queue=[]
        let cnt=0

        console.log(inDeg)

        for(let i=0;i<inDeg.length;i++){
            if(inDeg[i]===0){
                queue.push(i)
            }
        }

        while(queue.length){
            // console.log('queue')
            let x=queue[0]
            queue.shift()
            cnt++

            // 解放这个节点，其出边的节点入度-1
            for(let i=0;i<arr[x].length;i++){
                inDeg[arr[x][i]]--

                if(inDeg[arr[x][i]]===0){
                    queue.push(arr[x][i])
                }
            }

        }
        // console.log(cnt)

        return cnt
    }

    // 加边
    for(let i=0;i<prerequisites.length;i++){

        let target=prerequisites[i][0]
        let source=prerequisites[i][1]

        arr[source].push(target)
        inDeg[target]++

        // 开始拓扑排序，也即bfs找环
    }
    let res=tpSort()

    return res===numCourses
};

posted @ 2023-02-03 13:11 凌歆阅读(31) 评论(0) 收藏举报

刷新页面返回顶部

树与图

589. N 叉树的前序遍历

解题思路

递归

迭代

429. N 叉树的层序遍历

解题思路

完整代码

297. 二叉树的序列化与反序列化

解题思路

完整代码

105. 从前序与中序遍历序列构造二叉树

解题思路

完整代码

236. 二叉树的最近公共祖先

解题思路

完整代码

684. 冗余连接(模板题)（用于找环的模板）

无向图找环

解题思路

完整代码

207. 课程表

解题方法

dfs

bfs 找环法

公告