数组-链表-栈-队列

变长数组

• 实现方法（三步）

• 初始化，分配常数空间

• 在插入元素的过程中，如果空间不够，新建一个2倍原来空间长度的数组，把原数组的值拷贝到扩容的数组中，释放原数组空间

• 如果扩容后元素有删除的情况，但总元素个人少于数组长度25，释放一半的空间

• 时间复杂度分析（这里n>length才扩容，解释不是非常合理，理解就行）

  • 例如n=5

  数组	插入	拷贝
  [null]	0	0
  [1]	1	0
  [1,2]	2	1(次数) 1（元素个数）
  [1,2,3,null]	3	1(次数) 2 （元素个数）
  [1,2,3,4]	4	0 0
  [1,2,3,4,5,null,null,null]	5	1(次数) 4 (元素个数)

  • 分析
    • 长度为2是，拷贝1次，转移1个元素
    • 长度为3时，拷贝1次，转移2个元素
    • 长度为5时，拷贝1次，转移4个元素
  • 1+3+5 =n+n/2+n/4 即差不多（因为空数组没有另外计算了）

• 对于其他的n ，n+n/2+n/4+.... <=2n

• 一次扩容到下一次释放的最小的删除次数（一次删一个）0.5n（这里使用n=4时进行扩容）

  • 例如上题的n=4
  • n=4时扩容了一次，2n=8
  • 还需要删除2，4-2=2（25%,即0.5n）

注意点

• 可以是n=5是进行扩容
• 也可以是n=4（到达数组长度就进行扩容），这样上述的解释更合理
• 取决于你如何设计，但复杂度分析还是大差不差的

LeetCode

88. 合并两个有序数组

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

提示：

• nums1.length == m + n
• nums2.length == n
• 0 <= m, n <= 200
• 1 <= m + n <= 200
• -109 <= nums1[i], nums2[j] <= 109

进阶：你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗？

朴素算法

/**
 * @param {number[]} nums1
 * @param {number} m
 * @param {number[]} nums2
 * @param {number} n
 * @return {void} Do not return anything, modify nums1 in-place instead.
 */
var merge = function(nums1, m, nums2, n) {
 
    // 合并两个有序数组
    // 升序排列
 
    // 1.朴素算法 
    // 定义一个m+n长度的数组，存放排序好的
 
    // 定义三个指针，分别是nums1移动下标，nums2的移动下标
 
    let res=[]
 
    let p1=0
    let p2=0
    // let p3=0
 
    while(p1<m&&p2<n){
        if(nums1[p1]>nums2[p2]){
            res.push(nums2[p2])
            // console.log(nums2[p2])
            p2++
        }else {
            res.push(nums1[p1])
            // console.log(nums1[p1])
            p1++
        }
    }
 
    while(p1<m){
        res.push(nums1[p1])
        // console.log(nums1[p1])
        p1++
    }
 
    while(p2<n){
        res.push(nums2[p2])
        // console.log(nums2[p2])
        p2++
    }
 
    // console.log(res)
 
    for(let k=0;k<m+n;k++){
        nums1[k]=res[k]
    }
 
    // return res
    
 
};

• 时间复杂度：O(m+n) 准确 2*（m+n）
• 空间复杂度：O(m+n)

优化版本

/**
 * @param {number[]} nums1
 * @param {number} m
 * @param {number[]} nums2
 * @param {number} n
 * @return {void} Do not return anything, modify nums1 in-place instead.
 */
var merge = function(nums1, m, nums2, n) {
 
    // 合并两个有序数组
    // 升序排列
 
    
    // 2. 优化版本
 
    // 从nums1的最后下标开始，选取大的放入
 
    // 定义两个指针，分别指向 nums1，nums2的最后一个元素
 
    let i=m-1
    let j=n-1
    let k=m+n-1
    for(;k>=0;k--){
 
        // 出口，如果i或者j小于0
        if(i<0||j<0){
            break;
        }
 
        if(nums1[i]>nums2[j]){
            nums1[k]=nums1[i]
            i--
        }else{
            nums1[k]=nums2[j]
            j--
        }
    }
 
    // i最大的全部被挑选了
    while(j>=0){
        nums1[j]=nums2[j]
        j--
    }
 
    // j最大的全部被挑选了
    // while(i>=0){
    //     // 什么都不用做，因为i对于数组有序
    // }
 
};

• 时间复杂度O(m+n) 准确m+n
• 空间复杂度O(1)

堆排版本(更适用于有n个有序数组的合并)

1. 使用最大堆
2. 先把每个数组头[0]入堆
3. 开始最小的出堆，同时把其后面一个元素入堆[0+1(可变)]
4. 直到堆为空

• 需要维护一个指针数组，每个数组的后继元素
• 以本题为例
  • 时间复杂度mlog(2)+m+nlog(2)+n ,2O(m+n)
  • 空间复杂度 2(数组个数)

26. 删除有序数组中的重复项（模板题）

给你一个 升序排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。

由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。

将最终结果插入 nums 的前 k 个位置后返回 k 。

不要使用额外的空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

判题标准:

系统会用下面的代码来测试你的题解:

int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案
 
int k = removeDuplicates(nums); // 调用
 
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
    assert nums[i] == expectedNums[i];
}

如果所有断言都通过，那么您的题解将被 通过。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

提示：

• 1 <= nums.length <= 3 * 104
• -104 <= nums[i] <= 104
• nums 已按 升序 排列

解题思路

1.数组升序,原地去重
2.找出数组中所有不同的元素
3.遍历数组，判断数组元素不相同
4.数组元素不相同（因为数组有序，则分界点[i-1] - [i] 不同）
 

• 5.思想：
  不同则选取

完整代码

class Solution {
    public int removeDuplicates(int[] nums) {
        // 思路，遍历数组，判断是否需要保留该数
        int cnt=0;
        for(int i=0;i<nums.length;i++){
            if(i==0){
                cnt++;
                continue;
            } 
            if(nums[i]!=nums[i-1]){
                nums[cnt]=nums[i];
                cnt++;
            }
        }
 
        return cnt;
    }
}

283. 移动零(模板题)

• 该题与上题26-删除有序数组的重复思想相同（满足条件则选取）

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

示例 2:

输入: nums = [0]
输出: [0]

提示:

• 1 <= nums.length <= 104
• -231 <= nums[i] <= 231 - 1

进阶：你能尽量减少完成的操作次数吗？

完整代码

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
 
        // 解题思路
        // 满足条件的放前面
        int n=0;
        for(int i=0;i<nums.size();i++){
            if(nums[i]!=0){
                nums[n]=nums[i];
                n++;
            }
        }
 
        for(;n<nums.size();n++){
            nums[n]=0;
        }
    }
};

206. 反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

提示：

• 链表中节点的数目范围是 [0, 5000]
• -5000 <= Node.val <= 5000

进阶：链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

解题思路

1. 反转链表，即每个节点指向需要发生改变
2. 需要改n次
3. 遍历该链表
4. 每到达一个节点，改变指向为前一个节点，（同时把该节点存储为前一个节点）（方便后面元素使用）

完整代码

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var reverseList = function(head) {
 
    // 更换链条的顺序，更换n次
 
    let pre=null;
 
    for(let p=head;p!=null;){
        let nextNode=p.next
 
        p.next=pre
 
        pre=p
 
        
        p=nextNode
    }
 
    return pre;
 
};

136. 邻值查找（可选）

给定一个长度为 nn 的序列 AA，AA 中的数各不相同。

对于 AA 中的每一个数 AiAi，求：

min1≤j<i|Ai−Aj|min1≤j<i|Ai−Aj|

以及令上式取到最小值的 jj（记为 PiPi）。若最小值点不唯一，则选择使 AjAj 较小的那个。

输入格式

第一行输入整数 nn，代表序列长度。

第二行输入 nn 个整数A1…AnA1…An,代表序列的具体数值，数值之间用空格隔开。

输出格式

输出共 n−1n−1 行，每行输出两个整数，数值之间用空格隔开。

分别表示当 ii 取 2∼n2∼n 时，对应的 min1≤j<i|Ai−Aj|min1≤j<i|Ai−Aj| 和 PiPi 的值。

数据范围

n≤105n≤105,|Ai|≤109|Ai|≤109

输入样例：

3
1 5 3

输出样例：

4 1
2 1

解题思路

1. 从下标2开始，找在它前面的元素（元素的值-当前值最小），输出差值和找到元素的下标
2. 如果使用朴素算法 1*2*3*。。。*n n!

正确解法
1. 为每个元素先创建节点（val和下标）n
2. 对节点进行排序 nlog(n)
3. 把排序后的节点连接起来（双向链表）n
4. 定义一个数组，存储没有排序的节点
5. 从5数组的最后一个下标（一个节点->对应排序后双向链表中的一个节	点）开始，比较它的前驱和后继与该节点值的差值 n
	看那个小，输出该查找和较小的下标
6. 删除双向链表中数组5最后一个节点 1*n
7. 5的下标左移，重新循环5,6,7，直到下标=1

• 注意点

  • 从5数组的最后一个下标开始，因为可以保证它的前驱和后继的下标都在它前面
  • 删除5数组在双向链表中的对应节点（可以保证其他的元素节点的前驱和后继都是在本身下标的前面）
  • 比较它的前驱和后继与该节点值的差值 （因为排序后，节点附近的差值一定是最小的）

• 时间复杂度

  • n+nlogn+n+n+n ==>O(n+nlog(n))

• 空间复杂度

  • n+n==>O(n)

完整代码

let arr = [1, 5, 3]
 
// 存储节点，用于构建双向链表
function Node(val, index, pre, next) {
  this.val = val === undefined ? -1 : val
  this.index = index === undefined ? -2 : index
  this.pre = pre === undefined ? null : pre
  this.next = next === undefined ? null : next
}
 
// 创建保护节点
let head = new Node(-1, -1)
let tail = new Node(-2, -2)
 
head.next = tail
tail.pre = head
// 创建保护节点
 
// 创建元素节点
let nodeList = []
let nodeList2 = []
arr.forEach((item, index) => {
  let node = new Node(item, index)
  nodeList.push(node)
  nodeList2.push(node)
})
 
// 节点排序
nodeList.sort((a, b) => {
  return a.val - b.val
})
 
// 创建双向链表（排序后的）
let pTail = head
nodeList.forEach(item => {
  pTail.next = item
  item.pre = pTail
  pTail = pTail.next
})
 
nodeList[nodeList.length - 1].next = tail
tail.pre = nodeList[nodeList.length - 1]
 
 
// nodeList2 从最后一个元素开始
// 比较前驱和后继
for (let i = nodeList2.length - 1; i >= 1; i--) {
  let a = 0 // 前驱差值绝对值
  let b = 0 // 后继差值绝对值
  let res = 0 // 差值绝对值最小值
  let index = 0 // 找到的下标
  
  if (nodeList2[i].pre) {
    a = Math.abs(nodeList2[i].val - nodeList2[i].pre.val)
  }
 
  if (nodeList2[i].next) {
    b = Math.abs(nodeList2[i].val - nodeList2[i].next.val)
  }
 
  if (a > b) {
    res = b
    index = nodeList2[i].next.index
  } else if (a < b) {
    res = a
    index = nodeList2[i].pre.index
  } else {
    res = a
    index = Math.min(nodeList2[i].pre.index, nodeList2[i].next.index)
  }
 
  console.log(res, index + 1, i)
 
  // 把当前节点删除
  let pre1 = nodeList2[i].pre
  nodeList2[i].pre.next = nodeList2[i].next
  nodeList2[i].next.pre = pre1
}
 
console.log(nodeList)
 

142. 环形链表 II(可选)

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

• 链表中节点的数目范围在范围 [0, 104] 内
• -105 <= Node.val <= 105
• pos 的值为 -1 或者链表中的一个有效索引

进阶：你是否可以使用 O(1) 空间解决此题？

解题思路

• 快慢指针
  • 快的一次走两步
  • 慢的一次走一步
  • 如果存在环，必定相遇

1. 判断是否存在环，不存在，直接返回
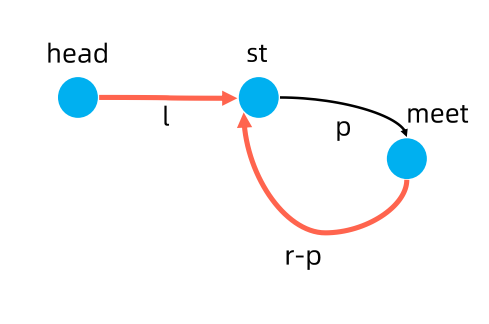
2. 存在，在相遇点，假设快指针走了l+p+kr(r为环的长度)，慢指针走了
l+p
3. 则2(l+p)=l+p+kr==》l=(k-1)*r+(r-p)
 
4. 即l=r-p+k倍环的长度
 
5.则head一次走一步，慢指针重相遇点一次走一步，必定在起点相遇
	

• 

完整代码

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
 
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var detectCycle = function(head) {
 
    // 定义一个是否有环的判断函数
 
    const hasCircle=(head)=>{
 
        let fast=head;
        let slow=head;
 
        while(fast!=null&&slow!=null&&fast.next!=null){
            fast=fast.next.next
            slow=slow.next
 
            if(fast===slow){
                return slow
            }
        }
 
        return null
    }
 
    let slow=hasCircle(head)
    if(!slow){
        return null
    }
 
    // 有环，返回起点的下标
 
    // head 和slow相遇点同时开始走，再次相遇就是start
 
    let p=head
    while(p!==slow){
        p=p.next
        slow=slow.next
    }
 
    return p
};

155. 最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

• MinStack() 初始化堆栈对象。
• void push(int val) 将元素val推入堆栈。
• void pop() 删除堆栈顶部的元素。
• int top() 获取堆栈顶部的元素。
• int getMin() 获取堆栈中的最小元素。

示例 1:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
 
输出：
[null,null,null,null,-3,null,0,-2]
 
解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

提示：

• -231 <= val <= 231 - 1
• pop、top 和 getMin 操作总是在 非空栈 上调用
• push, pop, top, and getMin最多被调用 3 * 104 次

解题思路

获取栈的最小值
1. 在每个元素入栈时比较，当前元素和栈顶元素的大小，把较小值存储起来
2. 弹栈时，栈顶元素出去，存储的较小值也出去

完整代码

 
// 解题思路
 
// 定义一个辅助栈
 
// 每次进来时，辅助站只存储栈的最小值
 
// 当获取栈的最小值时，最小值就在辅助栈栈顶
 
var MinStack = function() {
    this.stack=[]
    this.minStack=[Infinity]
};
 
/** 
 * @param {number} val
 * @return {void}
 */
MinStack.prototype.push = function(val) {
    this.stack.push(val)
    this.minStack.push(Math.min(this.minStack[this.minStack.length-1],val))
};
 
/**
 * @return {void}
 */
MinStack.prototype.pop = function() {
    this.stack.pop()
    this.minStack.pop()
};
 
/**
 * @return {number}
 */
MinStack.prototype.top = function() {
    if(this.stack.length){
        return this.stack[this.stack.length-1]
    }
 
    return undefined   
};
 
/**
 * @return {number}
 */
MinStack.prototype.getMin = function() {
    return this.minStack[this.minStack.length-1]
};
 
/**
 * Your MinStack object will be instantiated and called as such:
 * var obj = new MinStack()
 * obj.push(val)
 * obj.pop()
 * var param_3 = obj.top()
 * var param_4 = obj.getMin()
 */

150. 逆波兰表达式求值

根据 逆波兰表示法，求表达式的值。

有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

注意 两个整数之间的除法只保留整数部分。

可以保证给定的逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

提示：

• 1 <= tokens.length <= 104
• tokens[i] 是一个算符（"+"、"-"、"*" 或 "/"），或是在范围 [-200, 200] 内的一个整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

• 平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
• 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

• 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
• 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

完整代码

/**
 * @param {string[]} tokens
 * @return {number}
 */
var evalRPN = function(tokens) {
 
    // 后缀表达式求值
 
    // 存在最近相关性，一般用栈解决
 
    // 遇到数字，入栈
 
    // 遇到运算符，出栈两个运算数，结果压入栈中
 
    let stack=[]
 
    const compute=(ch)=>{
        let a=stack.pop()
        let b=stack.pop()
        switch(ch){
 
            case "+":
                return a+b
            break
            case "-":
                return b-a
            break
            case "*":
                return b*a
            break
            case "/":
                return Number.parseInt(b/a) 
            break  
        }
    }
 
    let chArr=["+","-","*","/"]
 
    tokens.forEach((item)=>{
        if(chArr.some(item1=>item1===item)){
            let res=compute(item)
            stack.push(res)
        }else{
            // 转换成数字
            let num=Number.parseInt(item)
            stack.push(num)
        }
    })
 
    console.log(stack)
 
    return stack[0]
 
};

224. 基本计算器

给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。

注意:不允许使用任何将字符串作为数学表达式计算的内置函数，比如 eval() 。

示例 1：

输入：s = "1 + 1"
输出：2

示例 2：

输入：s = " 2-1 + 2 "
输出：3

示例 3：

输入：s = "(1+(4+5+2)-3)+(6+8)"
输出：23

提示：

• 1 <= s.length <= 3 * 105
• s 由数字、'+'、'-'、'('、')'、和 ' ' 组成
• s 表示一个有效的表达式
• '+' 不能用作一元运算(例如， "+1" 和 "+(2 + 3)" 无效)
• '-' 可以用作一元运算(即 "-1" 和 "-(2 + 3)" 是有效的)
• 输入中不存在两个连续的操作符
• 每个数字和运行的计算将适合于一个有符号的 32位 整数

解题思路

1. 转换为后缀表达式
   遇到数字，入stack栈（后缀表达式的栈）
   遇到左括号，直接入符号栈
   遇到运算符，如果符号栈栈顶优先级>=当前运算符，符号栈出栈，元素    push到stack栈，直到条件不满足，将当前运算符入符号栈
   遇到右括号，出栈符号栈，元素push到stack栈，直到为左括号，左括号也出栈
   把符号栈剩下的元素都push到stack栈中

• 注意点
  • 连续数字的处理 parse_nums
    • 第一次数字，parse_nums, val=val*10+currVal
    • 直到不是数字
  • -号作为数字符号位的处理
    • 例如 -8 转换为0-8
    • 需要转换的情况
      • ( 后面的数字
      • +号-号后面的数字

完整代码

/**
 * @param {string} s
 * @return {number}
 */
var calculate = function (s) {
  // 获取优先级
  const getRand = ch => {
    if (ch === '+' || ch === '-') {
      return 1
    }
 
    if (ch === '(' || ch === ')') {
      return 0
    }
  }
 
  // 解题思路
 
  // 将中缀表达式转换为后缀表达式
 
  // 遇到数字，直接输出
 
  // 遇到左括号，直接入栈
 
  // 遇到运算符，如果运算符的优先级<=栈顶 将栈顶出栈，直到条件不满足，将运算符入栈
 
  // 遇到右括号，出栈所有符号，同时输出，出栈左括号
 
  // 处理特殊情况
  // need_zero 是否需要前补零 例如(-2+3)*7 ==> (0-2+3)*7
  // parse_nums 是否需要进行数字的拼接 (11+22)*3  1拼上1 2要拼上2
 
  let need_zero = true
  let parse_nums = false
  // 存储后缀表达式
  let stack = []
 
  // 存储操作符
  let ops = []
  // 存储parse的数值
  let val = 0
  for (let i = 0; i < s.length; i++) {
    let code = s.charCodeAt(i)
 
    // 为数字
    if (code >= 48 && code <= 57) {
      val = val * 10 + code - 48
      parse_nums = true
      continue
    } else if (parse_nums) {
      // 数字后面遇到不是数字的
      parse_nums = false
      // 不需要补零 (10-2) (10+2)
      need_zero = false
      // 把parse好的数字入栈
      stack.push(val.toString())
      val = 0
    }
 
    // 为空格
    if (s[i] === ' ') {
      continue
    }
 
    // 为符号
 
    if (s[i] === '(') {
      ops.push(s[i])
      // 左括号在数字前面，需要补零（-2+3）==>(0-2+3)
      need_zero = true
      continue
    }
 
    if (s[i] === ')') {
      // 直接输出，直到左括号
 
      while (true) {
        let op = ops.pop()
 
        if (op === '(') {
          // ops.pop()
          break
        } else {
          stack.push(op.toString())
        }
      }
      // 右括号 (xxx)+2 (xxx)-2
      need_zero = false
      continue
    }
 
    // 如果是+ - 号
 
    // 走到这里，说明符号是正负号，需要处理补零的
    if (need_zero) {
      stack.push('0')
      // need_zero=false
    }
 
    // 判断栈顶和运算符的优先级
 
    // 栈顶大于新来的
    while (ops.length && getRand(ops[ops.length - 1]) >= getRand(s[i])) {
      let op = ops.pop()
      stack.push(op)
    }
 
    ops.push(s[i])
    need_zero = true // + -号也需要补零 48+-49  18-+48
  }
 
  // 如果parse_nums=true 还在parse
  // 直接入栈
  if (parse_nums) {
    stack.push(val.toString())
  }
 
  while (ops.length) {
    stack.push(ops.pop())
  }
 
  // 得到后缀表达式
  console.log(stack)
}
 
calculate('(1+(4+5+2)-3)+(6+8)')