Paper Reading：DOFEN: Deep Oblivious Forest ENsemble

目录

• 研究动机
• 文章贡献
• 预备知识
  • Oblivious Decision Tree
  • Heaviside函数
• 本文方法
  • ODT 松弛化
  • DOFEN 模型架构
    • 条件生成
    • Relaxed ODT 构建
    • 两级 Relaxed ODT 集成
  • DOFEN 模型设置
• DOFEN 和 ODF 的对应关系的理解
• 实验结果
  • 数据集和实验设置
  • 性能评估
  • 模型稳定性
  • 个体rODT的权重分析
  • 计算效率分析
  • 模型可解释性分析
    • 消融实验
  • 超参数分析
• 优点和创新点

Paper Reading 是从个人角度进行的一些总结分享，受到个人关注点的侧重和实力所限，可能有理解不到位的地方。具体的细节还需要以原文的内容为准，博客中的图表若未另外说明则均来自原文。

论文概况	详细
标题	《DOFEN:Deep Oblivious Forest ENsemble》
作者	Kuan-Yu Chen, Ping-Han Chiang, Hsin-Rung Chou, Chih-Sheng Chen, Darby Tien-Hao Chang
发表会议	Advances in Neural Information Processing Systems 37 (NeurIPS 2024)
发表年份	2024
会议等级	CCF-A
论文代码	https://github.com/Sinopac-Digital-Technology-Division/DOFEN

作者单位：

1. Sinopac Holdings
2. National Cheng Kung University

研究动机

尽管 DNN 在图像、文本等领域取得了巨大成功，但是在表格数据领域，梯度提升决策树等树模型长期以来在性能上显著优于深度神经网络。GBDT 等树模型在构建每个基学习器（决策树）时，仅会稀疏地选择一部分特征，这不仅增强了特征的多样性，还有效地防止了过拟合。主流的表格 DNN 无法实现真正的稀疏选择，例如基于注意力机制的模型（如 Transformer 变体）通过 Softmax 操作聚合所有特征信息，本质上是一种“稠密选择”；而一些尝试使用Sparsemax等方法逼近稀疏性的模型，也仅能实现“近似稀疏”的效果，而非真正的开关式选择。因此识别并明确指出“缺乏真正的稀疏特征选择机制”是限制现有表格 DNN 性能超越树模型的一个根本性障碍。直接生成用于开关式列选择的稀疏矩阵是一个不可微的操作，无法融入基于梯度下降的神经网络训练流程。为此，可以通过一个创新的两阶段解决思路来绕过这一难题：

1. 枚举（Enumeration）：尽可能多地生成各种可能的稀疏列选择组合。
2. 加权（Weighting）：通过一个可微分的神经网络来学习并为这些组合分配重要性权重。

文章贡献

受到遗忘决策树的启发，本文提出了一个用于处理表格数据深度神经网络架构 DOFEN。DOFEN 首先通过随机组合条件来构建一个庞大的、可微分的松弛 ODT 池，然后引入一个独特的两级集成策略：第一级通过随机采样 rODT 形成多个独立的森林以引入多样性并防止过拟合，第二级则将这些森林的预测结果进行聚合，最终输出预测。这种设计使 DOFEN 能够有效模拟树模型的优势，同时保持神经网络的端到端可训练性。通过在 Tabular Benchmark 上的实验，本文证明了 DOFEN 的表现不仅显著优于其他深度学习方法，而且与强大的梯度提升决策树模型具有竞争力。

预备知识

Oblivious Decision Tree

Oblivious Decision Tree 是一种特殊类型的决策树，它在树的每一层（同一深度）都使用完全相同的特征和分裂阈值。在标准的决策树（如 CART、ID3）中，每个内部节点（非叶子节点）都可以基于任何一个特征进行分裂。这意味着第一层的一个节点可能根据特征 A 进行分裂，同一层的另一个节点可能根据完全不同的特征 B 进行分裂。分裂点的选择是局部的、贪婪的，旨在最好地分割到达该节点的数据。Oblivious Decision Tree 对标准决策树施加了一个强大的结构性约束：在树的每一层，所有节点都必须使用相同的特征和相同的分裂阈值。这意味着第一层的所有节点都根据特征 A 和阈值 T1 进行分裂，第二层的所有节点都根据特征 B 和阈值 T2 进行分裂，以此类推。如此，树就变成了一种“对称”或“平衡”的结构，无论数据如何，从根节点到任何叶子节点的路径长度都是相同的，并且路径上评估的特征顺序也是固定的。

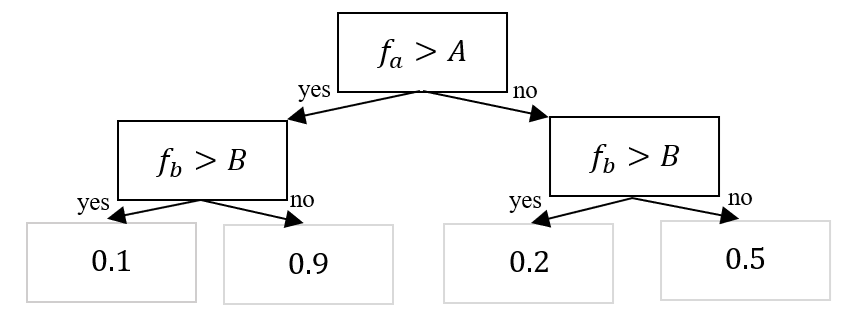
Oblivious Decision Tree 包含以下优点：

1. 推理速度极快：由于树的每一层只检查一个特征，整个推理过程可以转化为一系列简单的“if-else”判断，或者甚至可以通过位操作来并行处理。
2. 模型尺寸小：只需要存储每个层使用的特征和阈值，而不需要存储整个树结构。模型大小与树的深度成线性关系，而不是与节点数量成指数关系。
3. 正则化效果：这种结构性约束本身就是一种强大的正则化，可以有效防止过拟合。
4. 易于解释：虽然不如单棵标准决策树那么直观，但其对称结构使得模型行为相对规整，更容易从整体上理解特征的重要性。

Oblivious Decision Tree 包含以下缺点：

1. 模型表达能力受限：由于强结构约束，Oblivious Tree 的拟合能力通常不如同等深度的标准决策树，它可能无法捕捉数据中一些复杂的、非对称的交互关系。
2. 训练更困难：找到每一层“最优”的特征和阈值是一个组合优化问题，比标准决策树的贪婪训练算法要复杂得多，通常需要使用梯度下降或其他优化技术来近似求解。

Heaviside函数

Heaviside 函数是一个最简单的“开关”函数，它将所有负输入映射为 0，将所有正输入映射为 1。通常用 \(H(x)\) 或 \(Theta(x)\) 表示，最常见的定义是：

\[H(x) = \begin{cases} 0 & \text{if } x < 0 \\ 1 & \text{if } x \ge 0 \end{cases}\]

Sign 函数（符号函数）是 Heaviside 函数的“中心化”版本，它将负输入映射为 -1，正输入映射为 +1，它们之间的关系是：\(H(x) = \frac{\text{sgn}(x) + 1}{2}\)。Sigmoid 函数（逻辑斯蒂函数）可以看作是 Heaviside 函数的“光滑近似”，Sigmoid函数有一个平滑的 S 形曲线，而不是一个突兀的跳跃。因为 Sigmoid 处处可导，使得基于梯度的优化成为可能，可以说 Sigmoid 是“软化”或“光滑化”的 Heaviside 函数。

本文方法

ODT 松弛化

首先将不可微的 Oblivious Decision Tree (ODT) 松弛化，使其能够整合到神经网络中进行端到端训练。一个传统的 ODT 对输入向量 \(\vec{x} \in R^{N_{\text{col}}}\) 进行操作，其核心是一个由 \(d\) 个条目组成的决策表。每个条目对应树的一个深度，包含一个选定的列索引 \(I_j\)、该列的值 \(x_{I_j}\) 以及一个阈值 \(b_j\)，最终通过 Heaviside 函数 \(H\) 输出决策结果。其数学表达如下：

\[\begin{align*}\operatorname{ODT}(\vec{x})=&\left\{H\left(x_{I_{j}}-b_{j}\right)\right\},\vec{x}\xrightarrow{\text{ decided by entropy, Gini impurity, etc.}}\left\{\left(x_{I_{j}}, b_{j}\right)\right\},\\ & I_{j}\in\left\{1,2,\ldots, N_{\text{col}}\right\}, b_{j}\in R, j=(1,2,\ldots, d)\end{align*} \]

然而，ODT 中的列选择、阈值决策和 Heaviside 函数都是非微分的操作，这阻碍了其直接融入基于梯度下降训练的神经网络。为了解决这个问题，DOFEN 提出了一种松弛方法，将 ODT 转化为可微的 relaxed ODT（rODT）。具体来说 rODT 在各深度随机选择列，而非基于信息增益等准则。对于选定的列 \(I_j\)，其阈值 \(b_j\) 和 Heaviside 函数 \(H\) 被一个子网络 \(\Delta_{1 I_{j}}\) 所取代。该子网络使用 sigmoid 等激活函数来生成软条件（soft conditions），从而实现可微性。松弛后的 rODT 数学表达式为：

\[\begin{array}{l}rODT(\vec{x})=\left\{\Delta_{1 I_{j}}\left(x_{I_{j}}\right)\right\},\vec{x}\xrightarrow{\text{ randomly select}}\left\{x_{I_{j}}\right\},\\ I_{j}\in\left\{1,2,\ldots, N_{col}\right\}, j=(1,2,\ldots, d)\end{array} \]

DOFEN 模型架构

DOFEN 模型的整体架构由三个核心模块构成，实现生成大量 rODT 并对其进行有效的集成。

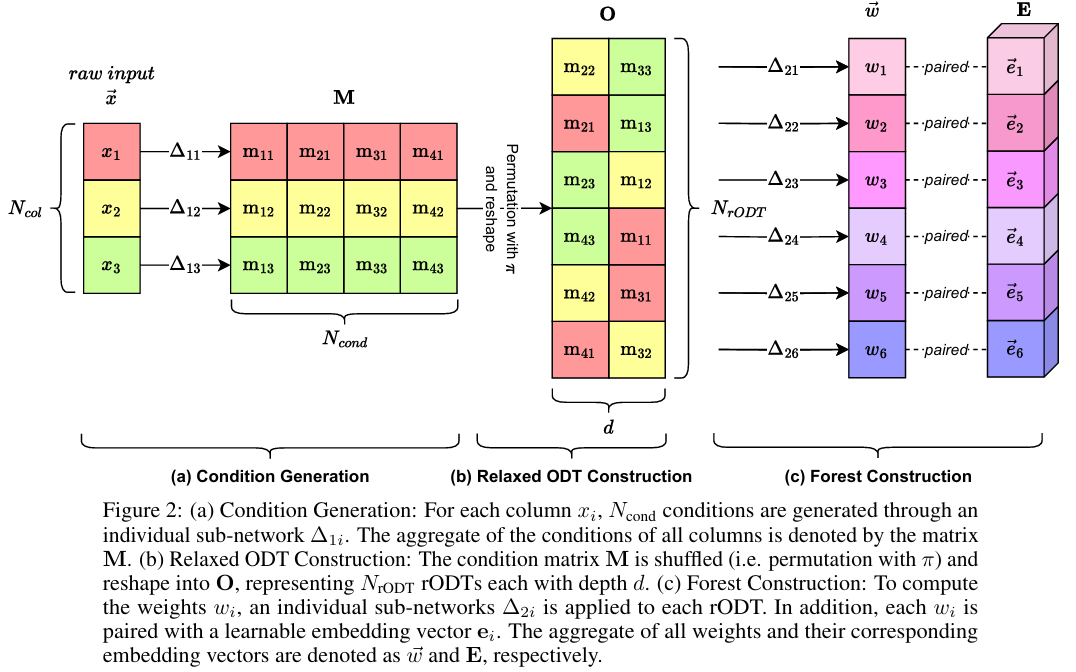
条件生成

该模块的核心目标是将原始的输入数据转换为一个条件矩阵 \(M\)，这里的每个“条件”是一个标量，用于表示一个特定的列（特征）在多大程度上满足某个决策规则。模块的输入是原始的表格数据向量 \(\vec{x}\)，其中包含数值型和类别型的列。为了处理类别型特征，DOFEN 使用了嵌入层（embedding layers）将其转换为数值表示。对于输入向量中的每一个列 \(x_i\)，DOFEN 都使用一个独立的子网络 \(\Delta_{1i}\) 进行处理。这个子网络是一个嵌入层（针对类别列）或一个线性层（针对数值列）。每个 \(\Delta_{1i}\) 会为该列生成 \(N_{\text{cond}}\) 个条件。因此，对于一个有 \(N_{\text{col}}\) 个列的数据集，最终会生成一个大小为 \(N_{\text{cond}} \times N_{\text{col}}\) 的条件矩阵 \(M\)。该矩阵的数学定义如下：

\[M=\begin{bmatrix}m_{11}&\ldots&m_{1N_{\text{col}}}\\ \vdots&\ddots&\vdots\\ m_{N_{\text{cond}}1}&\ldots&m_{N_{\text{cond}}N_{\text{col}}}\end{bmatrix}\in R^{N_{\text{cond}}\times N_{\text{col}}},(m_{i1},\ldots,m_{iN_{\text{cond}}})=\Delta_{1i}(x_{i}),i=(1,2,\ldots,N_{\text{col}}) \]

这个设计源于 ODT 的原理，即决策树中的每个节点条件都只依赖于一个单一的特征。通过为每个特征生成多个条件，DOFEN 实际上是在创建一组丰富的、可学习的决策规则候选池。

Relaxed ODT 构建

该模块的核心目标是将条件生成模块（Condition Generation）输出的条件矩阵 \(M\) 转换为多个可微分的 rODT，每个 rODT 代表一个具有深度 \(d\) 的决策表。与传统的 ODT 基于预定义准则（如熵或基尼不纯度）选择特征和阈值不同，DOFEN 采用了一种随机策略来构建 rODT。具体而言，该模块从条件矩阵 \(M\) 中随机选择 \(d\) 个条件（不重复）来构建一个 rODT。矩阵 \(M\) 的维度为 \(N_{\text{cond}} \times N_{\text{col}}\)，其中 \(N_{\text{cond}}\) 是每列生成的条件数，\(N_{\text{col}}\) 是数据集的列数。

为了系统化地实现这一随机选择过程，DOFEN 采用了一种“洗牌-重塑”（shuffle-then-reshape）的操作。首先，将矩阵 \(M\) 中的所有元素进行随机排列，使用一个双射函数 \(\pi\) 表示。然后将排列后的元素重新塑形为一个新的矩阵 \(O\)，其维度为 \(N_{\text{rODT}} \times d\)。这个过程可以用以下数学公式描述：

\[O = \begin{bmatrix} o_{11} & \ldots & o_{1d} \\ \vdots & \ddots & \vdots \\ o_{N_{\text{rODT}}1} & \ldots & o_{N_{\text{rODT}}d} \end{bmatrix} \in \mathbb{R}^{N_{\text{rODT}} \times d} \]

其中，矩阵 \(O\) 的每个元素 \(o_{jk}\) 与矩阵 \(M\) 中的元素 \(m_{uv}\) 对应，映射关系由下式定义：

\[\{ o_{jk} \mid j = \lceil \frac{\pi(n)}{d} \rceil, k = \pi(n) \mod d, n = u \times N_{\text{col}} + v \} = \{ m_{uv} \} \subset M \]

这里，\(1 \leq u \leq N_{\text{cond}}\)，\(1 \leq v \leq N_{\text{col}}\)。矩阵 \(O\) 的每一行代表一个完整的 rODT，包含了从根节点到叶子节点路径上的 \(d\) 个决策条件。
在实现中，rODT 的数量 \(N_{\text{rODT}}\) 由公式 \(N_{\text{rODT}} = N_{\text{cond}} N_{\text{col}} / d\) 决定。为了确保 \(N_{\text{rODT}}\) 是整数，作者引入了一个中间参数 \(m\)，使得 \(N_{\text{cond}} = m d\)。在实践中，通过调整 \(m\) 来间接控制 \(N_{\text{cond}}\) 的大小。为了保持训练过程中的稳定性，排列操作（即洗牌步骤）仅在模型构建时执行一次，其配置在整个训练过程中保持不变。这种设计确保了每个 rODT 的结构一致性，同时通过初始的随机化保证了 rODT 池的多样性。

两级 Relaxed ODT 集成

两级集成策略的核心思想是模仿传统集成学习（如 Bagging）中的“重采样”思想，但在深度学习的框架下进行实现。其整体流程如下图所示，该过程主要分为两个层次：

1. 森林构建（Forest Construction）：从整个 rODT 池中随机抽取一个子集，形成一个独立的 rODT 森林。
2. 森林集成（Forest Ensemble）：构建多个这样的森林，并将它们的预测结果进行聚合，得到最终输出。

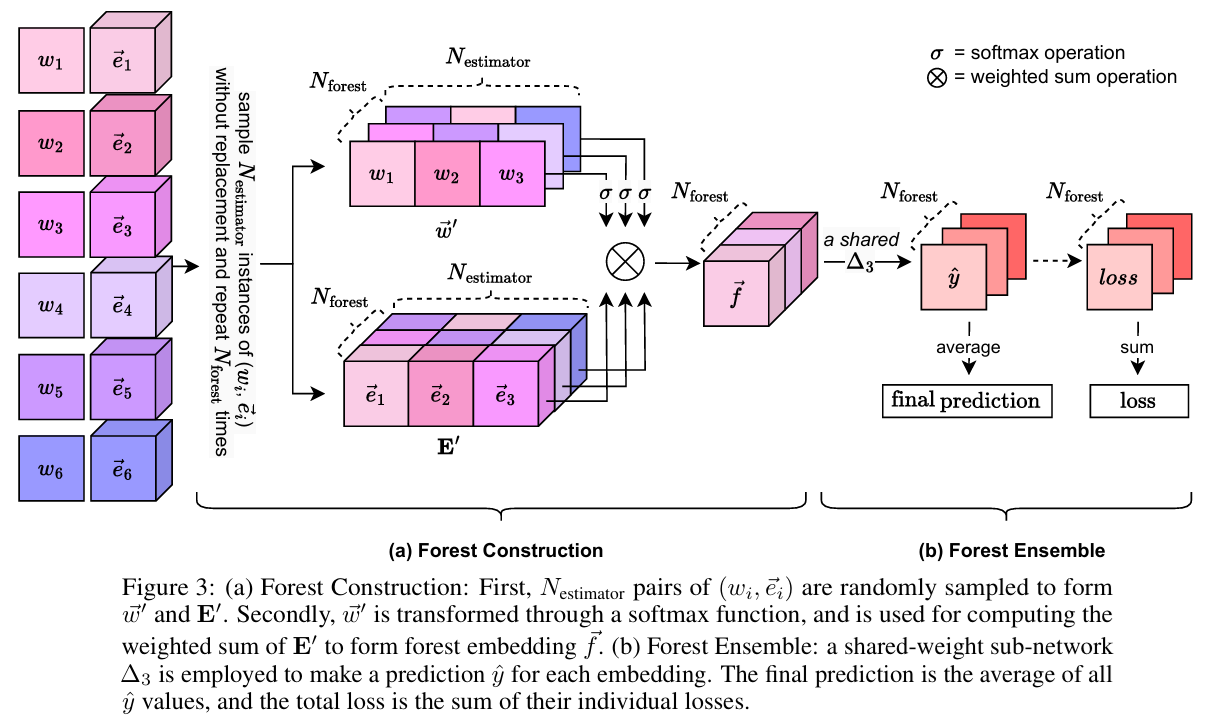
在森林构建这一级中，DOFEN 的目标是构建 \(N_{\text{forest}}\) 个rODT森林。每个森林的构建包含为每个 rODT 分配权重和嵌入向量和随机采样和森林嵌入两个步骤。对于一个输入样本，每个 rODT 都会被分配一个权重（\(\vec{w}\)），表示该样本与 rODT 决策规则的匹配程度。权重向量 \(\vec{w}\) 通过一个子网络 \(\Delta_{2}\) 计算得到，其维度为 \(N_{\text{rODT}}\)：

\[\vec{w} = \begin{pmatrix} \Delta_{21}((o_{11},\ldots,o_{1d})) \\ \vdots \\ \Delta_{2N_{\text{rODT}}}((o_{N_{\text{rODT}}1},\ldots,o_{N_{\text{rODT}}d})) \end{pmatrix} = (w_{1},\ldots,w_{N_{\text{rODT}}}) \in \mathbb{R}^{N_{\text{rODT}}} \]

每个 rODT 还有一个与之关联的、独立于输入样本的嵌入向量\(\vec{e}_i\)，它代表了该 rODT 本身的信息。所有嵌入向量组成矩阵 \(E\)：

\[E = \left[ \begin{array}{c} \vec{e}_{1} \\ \vdots \\ \vec{e}_{N_{\text{rODT}}} \end{array} \right] \in \mathbb{R}^{N_{\text{rODT}} \times N_{\text{hidden}}}, \text{ where } \vec{e}_{i} \in \mathbb{R}^{N_{\text{hidden}}}, i = (1,2,\ldots, N_{\text{rODT}}) \]

在随机采样和森林嵌入步骤中，为了构建一个森林，需要从整个 rODT 池（即 \(\vec{w}\) 和 \(E\)）中随机地、无放回地抽取 \(N_{\text{estimator}}\) 对权重和嵌入向量，形成子集 \(\vec{w}'\) 和 \(E'\)。然后，使用 Softmax 函数对采样得到的权重 \(\vec{w}'\) 进行归一化，并将其与对应的嵌入向量 \(E'\) 进行加权求和，生成一个代表整个森林的嵌入向量 \(\vec{f}\)。这个加权求和操作可以理解为，根据当前样本与各rODT的匹配程度（由权重表示），来聚合这些 rODT 的“知识”，从而形成一个综合的森林级表示。

\[\vec{f} \leftarrow \sum_{i=1}^{N_{\text{estimator}}} \text{softmax}(\vec{w}') \circ E' \]

在第二级，DOFEN将第一级构建的多个森林的预测结果进行森林集成（Forest Ensemble）。将每个森林的嵌入向量 \(\vec{f}\) 输入一个共享权重的子网络 \(\Delta_{3}\) 中，得到该森林的预测结果 \(\hat{y}'\)。

\[\hat{y}' \leftarrow \Delta_{3}(\vec{f}) \]

最终的预测 \(\hat{y}\) 是所有森林预测 \(\hat{y}'\) 的平均值（即Bagging）。对于回归任务，\(\hat{y}\) 是一个标量；对于分类任务，它是一个向量。在训练过程中，模型的总损失是每个森林预测的损失（使用损失函数 \(\mathcal{L}\)，如交叉熵或均方误差）之和：

\[\hat{y} \leftarrow \frac{1}{N_{\text{forest}}} \sum \hat{y}' \]

\[\text{loss} \leftarrow \sum \mathcal{L}(\hat{y}', y) \]

这种将损失相加而非平均的设计，有助于在训练过程中平衡不同森林的贡献。该步骤的整体流程如以下伪代码所示。

这种两级集成策略为 DOFEN 带来了关键优势：

• 防止过拟合：直接使用整个 rODT 池（即单森林）会导致严重的过拟合。而通过随机采样构建多个森林，相当于对 rODT 池应用了 Dropout，引入了正则化效果，显著提升了模型的泛化能力。
• 增强稳定性与性能：该过程本质上是深度学习框架下的一种 Bagging 方法。通过在单次训练中构建多样化的森林，并聚合它们的预测，有效提升了模型的性能和稳定性。

DOFEN 模型设置

下表列出了 DOFEN 模型的关键超参数及其默认值、描述和计算关系。这些参数共同定义了模型的架构、容量和行为。\(m\) 和 \(d\) 是基础参数，它们决定了 \(N_{\text{cond}}\)。\(N_{\text{col}}\) 和 \(m\) 共同决定了整个 rODT 池的规模 \(N_{\text{rODT}}\)，这种设计使得模型容量能够自适应于数据集的复杂度。\(N_{\text{estimator}}\) 不是固定值，而是与特征数 \(N_{\text{col}}\) 的平方根成正比。这意味着对于特征更多的数据集，每个森林会包含更多的rODT，使模型结构更具弹性。

超参数	默认值	描述与功能
\(N_{\text{col}}\)	取决于数据集	数据集中特征列的数量。这是模型输入维度的基础。
\(d\)	4	单个松弛遗忘决策树（rODT）的深度。它决定了每个 rODT 所包含的决策条件数量。
\(m\)	16	一个中间参数，主要用于确保条件数 \(N_{\text{cond}}\) 是深度 \(d\) 的整数倍。它是一个重要的容量调节参数。
\(N_{\text{cond}}\)	\(m \times d\) (默认 64)	为数据集的每一列生成的软条件（决策规则）的数量。计算公式为 \(m\) 乘以 \(d\)。
\(N_{\text{rODT}}\)	\(N_{\text{col}} \times m\)	模型构建的松弛遗忘决策树（rODT）池的总大小。它代表了模型可以选择的"树"的总量。
\(N_{\text{estimator}}\)	\(\max\{2, \lfloor \sqrt{N_{\text{col}}} \rfloor \} \cdot \frac{N_{\text{cond}}}{d}\)	在每个rODT森林中随机采样的 rODT 数量。这个值会根据数据集的特征数 \(N_{\text{col}}\) 动态调整。
\(N_{\text{forest}}\)	100	构建的 rOD T森林的数量。这是实现两级集成、提升模型稳定性和性能的关键参数。
\(N_{\text{hidden}}\)	128	每个 rODT 对应的嵌入向量 \(\vec{e}_i\) 的维度。它定义了 rODT "知识"的表示空间大小。
\(N_{\text{class}}\)	取决于数据集	分类任务中的目标类别数量。决定了模型输出层的维度。
dropout_rate	0.0	Dropout 操作的丢弃率。默认值为 0 表示不进行丢弃，用于正则化以防止过拟合。

所有实验均使用相同的优化设置：

配置项	设置值/说明
优化器 (Optimizer)	AdamW
学习率 (Learning Rate)	1e-3
权重衰减 (Weight Decay)	0
批量大小 (Batch Size)	256
训练周期数 (Training Epochs)	500
学习率调度 (Learning Rate Scheduler)	未使用
早停 (Early Stopping)	未使用
分类损失函数	交叉熵损失 (Cross-Entropy)
回归损失函数	均方误差损失 (Mean Squared Error)

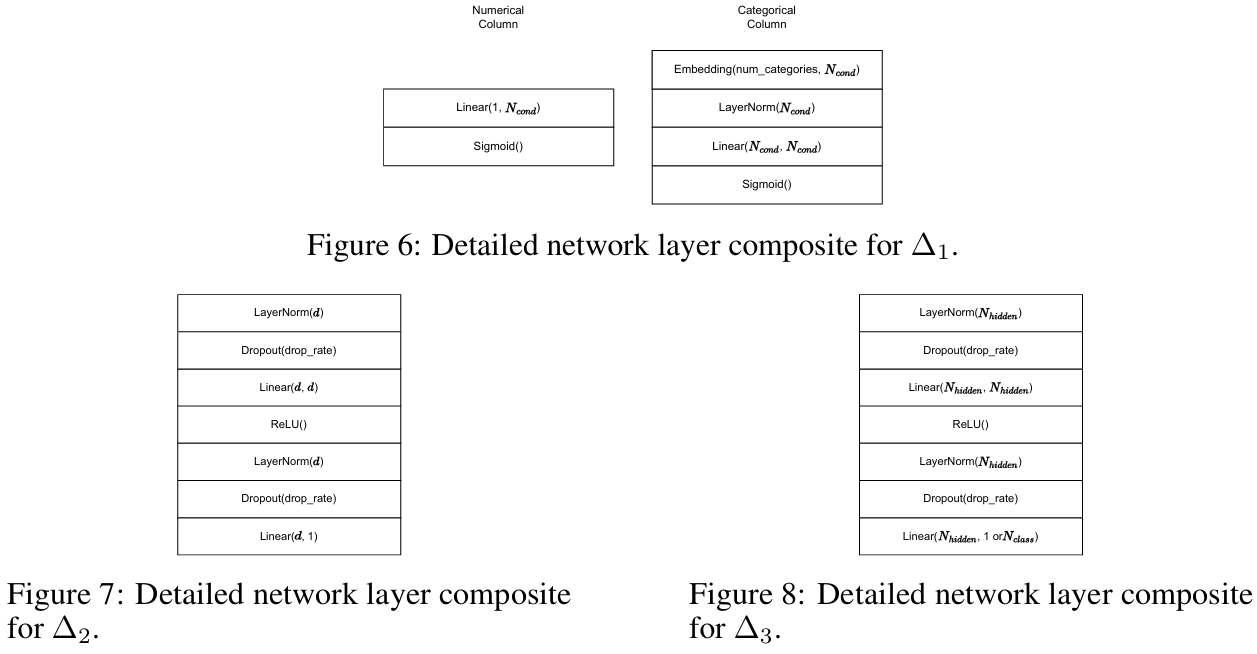
三个核心子网络 \(\Delta_1\), \(\Delta_2\), 和 \(\Delta_3\) 的模块功能和具体结构如下图所示。

1. \(\Delta_1\) - 条件生成：为每个输入列生成 \(N_{\text{cond}}\) 个软条件。对于数值型列，使用一个线性层；对于类别型列，使用一个嵌入层后接一个线性层。这意味着每个列都有自己独立的 \(\Delta_{1i}\) 网络进行处理。
2. \(\Delta_2\) - 权重生成：根据一个rODT所包含的 \(d\) 个条件，计算该rODT对于当前样本的权重 \(w_i\)。通常包含多层感知机、层归一化和 Dropout 等操作。其设计采用了组卷积来并行处理所有 rODT。
3. \(\Delta_3\) - 预测生成：将rODT森林的嵌入向量 \(\vec{f}\) 映射为最终的预测输出 \(\hat{y}\)。也是一个多层感知机结构，其输出维度根据任务而定（回归任务为 1，分类任务为 \(N_{\text{class}}\)）。

DOFEN 和 ODF 的对应关系的理解

DOFEN 模型与 ODT 的对应关系是其设计的核心，可以理解为 DOFEN 通过一种松弛化和结构化集成的策略，将传统 ODT 的硬决策过程转换为了一个可嵌入深度学习框架的可微分软决策系统。在决策规则方面：

• ODT：传统的遗忘决策树是一种硬决策模型。在每一层（深度）使用同一个特征及其阈值对所有样本进行划分。决策路径是确定性的、不可微的，通常基于信息增益等准则选择最优的特征和阈值。其决策过程可以简化为：如果 特征x > 阈值b, 则走右分支；否则走左分支。
• rODT：DOFEN 中的松弛 ODT 是 ODT 的可微分版本，它保留了ODT“每层条件统一”的结构性特点，但做了关键放松。rODT 每层所使用的特征（列）不再是基于贪心算法选择，而是随机指定的，通过“洗牌-重塑”过程实现；硬性的阈值比较和阶跃函数被替换为一个可微分的子网络 Δ₁，为每个输入值输出一个0到1之间的软分数，表示“该样本满足此决策条件”的程度。因此，一个 rODT 不再输出一个明确的二元决策路径，而是输出一组软条件分数，这些分数后续会被加权聚合。

在集成方式方面：

• ODT：在树集成算法（例如 CatBoost）中使用 ODT 作为弱学习器，通过梯度提升等方式进行集成，每个 ODT 是独立且顺序生成的。
• DOFEN：DOFEN 集成的是 rODT，但其集成方式更为复杂和结构化，体现为两级集成。第一级构建 rODT 森林，DOFEN 首先构建一个包含大量rODT的“池”，然后随机从池中抽取多个 rODT，并通过一个可学习的权重向量 w（由 Δ₂`子网络生成）进行加权求和，形成一个“森林嵌入向量”。第二级森林的集成，构建 rODT 森林的过程重复多次产生多个森林，每个森林的预测结果最后被平均（Bagging），得到最终输出。

信息表示方面：

• ODT：最终的预测信息存储在树的叶子节点值中。
• DOFEN：DOFE N摒弃了固定的叶子节点值。每个 rODT 都关联着一个可学习的嵌入向量 e，代表了该 rODT 的“知识”。在集成时，森林的表示是由各 rODT 的嵌入向量按其重要性权重聚合而成，最终的预测则由另一个子网络 Δ₃ 从这个聚合后的嵌入向量中解码出来。

总而言之，DOFEN 继承了 ODT 规整的、每层共享条件的树形结构作为其基本构建单元，但通过随机化特征选择和软化决策函数，将其转变为了可微分的 rODT。

实验结果

数据集和实验设置

为了确保评估的客观性和可比性，本研究严格遵循了Tabular Benchmark 的设置。使用的数据集如下，涵盖了分类和回归任务，特征类型包括纯数值型特征和数值-类别混合型特征。

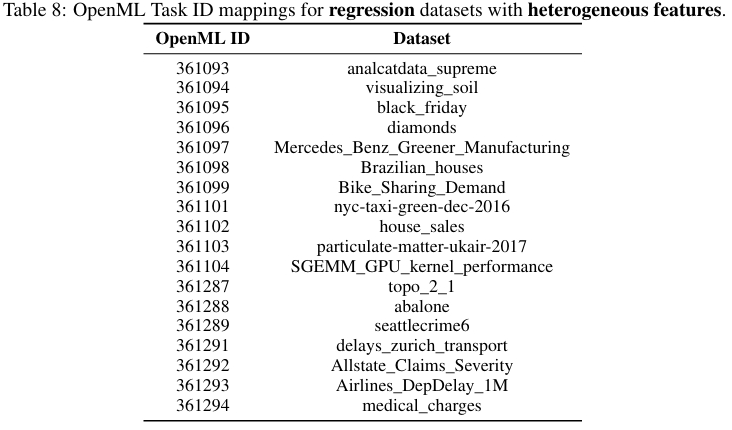
根据样本规模，数据集被进一步分为中等规模和大规模两类。

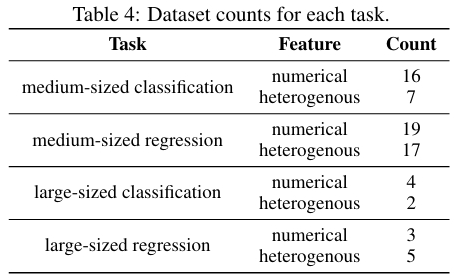
为了进行全面对比，实验选取的基线模型包括：

1. 树模型：RandomForest, GradientBoostingTree, HGBT, XGBoost, LightGBM, CatBoost。
2. 通用 DNN 模型：MLP, ResNet。
3. 前沿表格 DNN 模型：SAINT, FT-Transformer, NODE, Trompt, GRANDE。

其中，NODE 和 GRANDE 与 DOFEN 在高层次结构上相似，Trompt 被认为是当前最先进的表格 DNN 之一。

性能评估

正文重点展示了 DOFEN 在中等规模数据集上的性能，评估指标方面：分类任务使用准确率，回归任务使用 R 平方得分。实验结果如下图所示，DOFEN 在所有 DNN 基线模型中 consistently 排名第一或处于领先地位。它不仅在性能上可与树模型媲美，甚至在部分任务（如数值型分类）中超越了大多数树模型。在包含类别型特征的异构数据集上，DOFEN 的表现处于中等或偏下水平，反映了所有 DNN 模型在处理异构特征时面临的共同挑战。

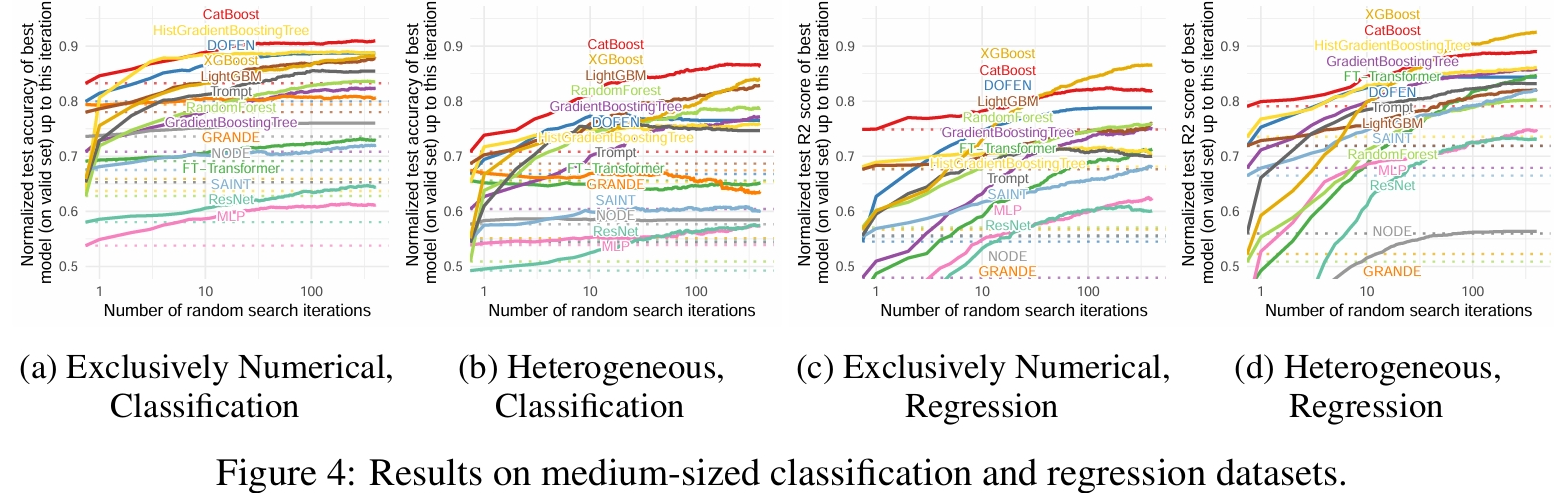
模型稳定性

DOFEN 在 rODT 构建和集成两个步骤中引入了随机性。如下表所示，当森林数量 \(N_{\text{forest}}\) 大于 10 时，模型在不同随机种子下的表现标准差非常小（约为均值的 0.01% 到 0.1%）。增加 \(N_{\text{forest}}\) 不仅能进一步提升稳定性，还能提高性能，证明了两级集成策略的有效性。实验表明，这种随机性并不会损害模型的稳定性。

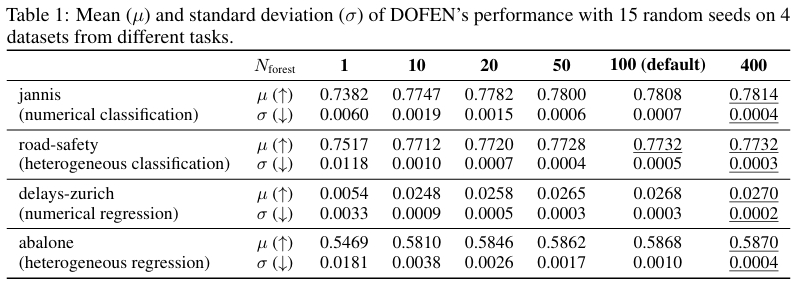
个体rODT的权重分析

通过分析 rODT 权重 \(w_i\) 在不同类别样本上的变化，研究发现权重标准差较大的 rODT 在分类中扮演更关键的角色。相反，权重变化小的 rODT 对样本不敏感。

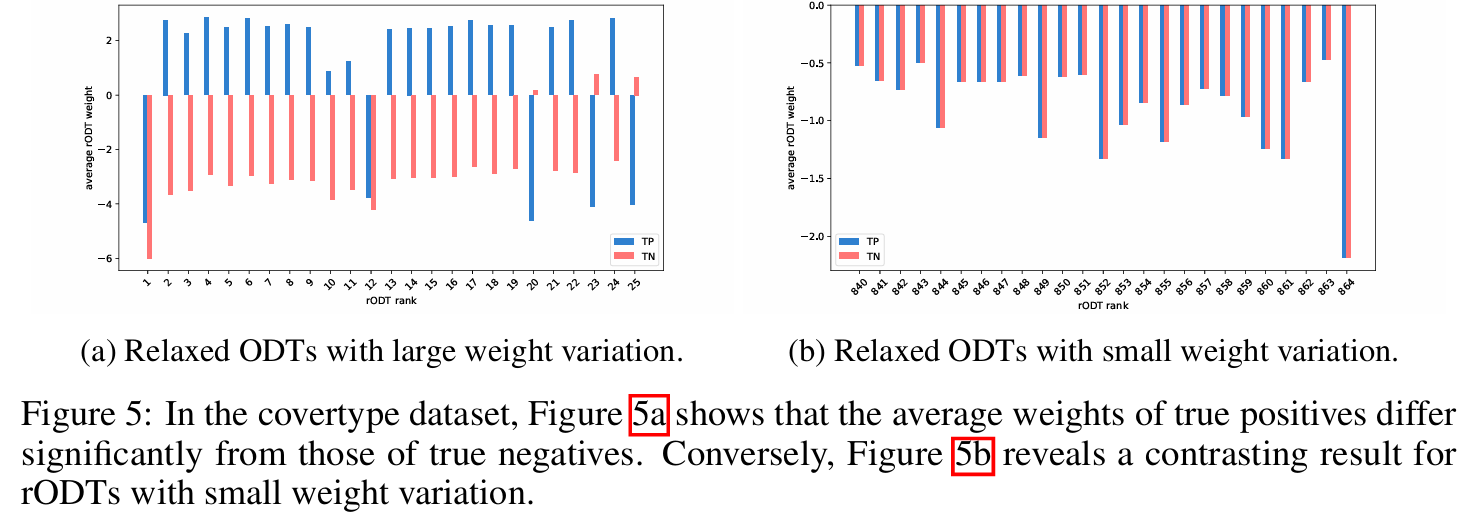
进一步实验表明，可以根据权重的标准差对 rODT 进行剪枝，移除不重要的 rODT 不仅能提高模型效率，甚至能轻微提升性能。

计算效率分析

DOFEN 在浮点运算次数和模型参数数量上均低于其他深度学习基线模型（如 Trompt、FT-Transformer），，但 DOFEN 的实际推理时间却相对较长。深入剖析发现，其瓶颈在于模型实现中使用的组卷积操作。具体来说，在森林构建模块中，用于并行计算每个 rODT 权重的子网络 \(\Delta_{2}\) 消耗了超过 85% 的推理时间，这是由于当前 PyTorch 框架对组卷积操作的优化不足所致。这属于工程实现层面的挑战，未来可以通过更优化的底层实现来改善。

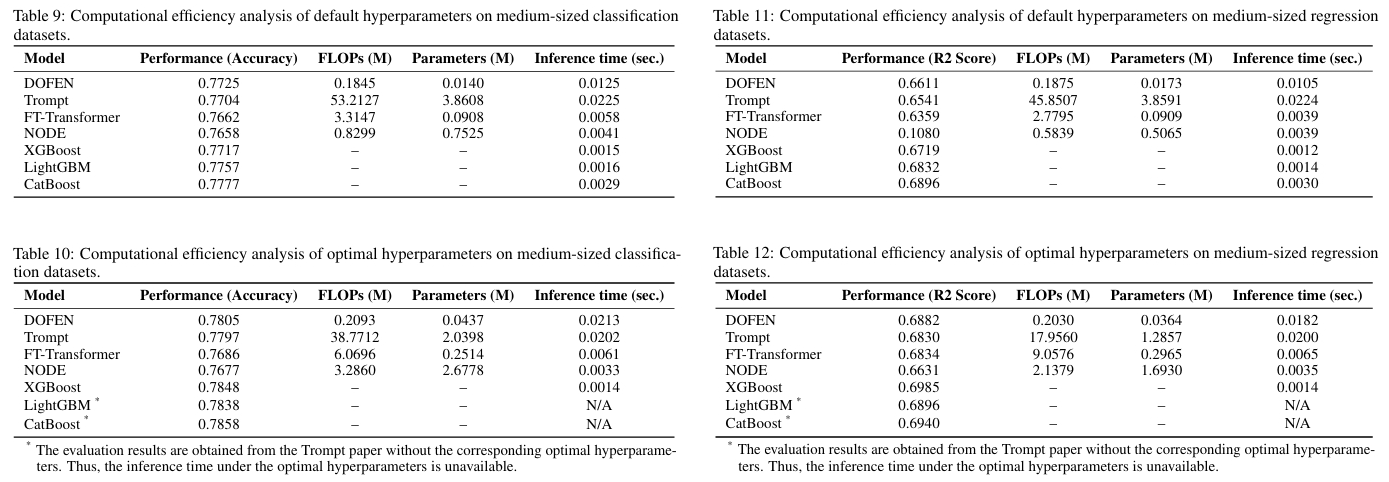
模型可解释性分析

DOFEN 的特征重要性计算方式类似于 LightGBM 或 XGBoost 中的“分裂重要性”，它通过计算一个样本的预测结果中，各个特征在所有被激活的 rODT 中的加权出现频率来得到。在多个真实数据集上的测试表明，DOFEN 识别出的前 3 个重要特征与主流树模型（如RandomForest、XGBoost、CatBoost 等）高度一致，仅在排名上略有差异，这证明了 DOFEN 的决策过程与树模型有相似之处，具备良好的可解释性，增强了模型的可信度。

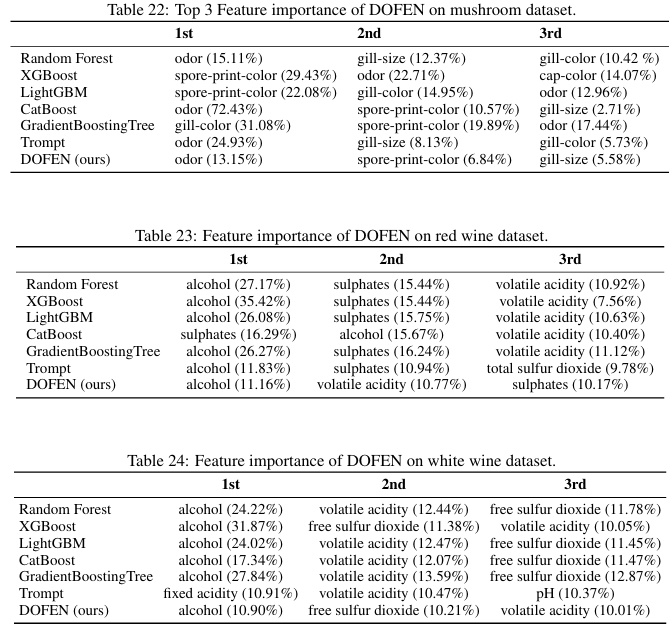
消融实验

两级集成的重要性方面，该实验移除了第二级集成（即不使用随机采样，而是用整个 rODT 池构建一个巨大的森林进行预测）。结果发现，这会导致模型严重过拟合，证明了两级集成中引入的随机性对于控制模型复杂度和确保泛化能力至关重要。

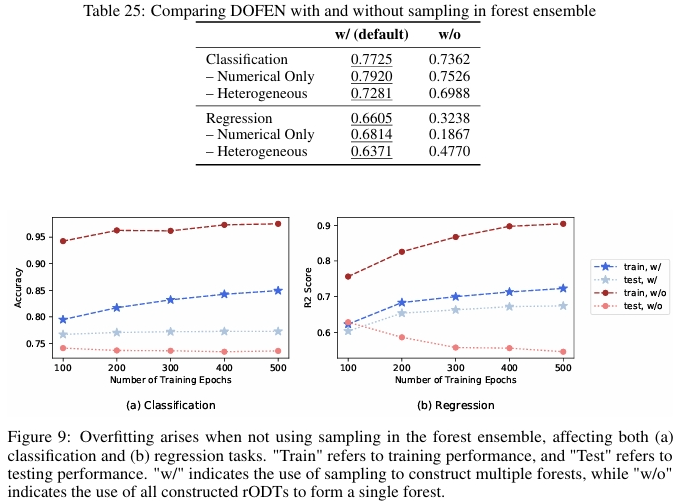
条件选择策略的对比方面，作者尝试用 CatBoost 模型学习到的特征选择结果来替代 DOFEN 中默认的随机“洗牌-重塑”策略，以构建 rODT。实验发现，这种基于预定义准则的方法性能略优于随机策略，但导致了非端到端的两阶段训练流程。

rODT 的剪枝分析方面，根据权重标准差对 rODT 进行剪枝。结果表明，剪枝掉权重变化不显著的 rODT 不仅能提高效率，甚至能轻微提升模型性能。

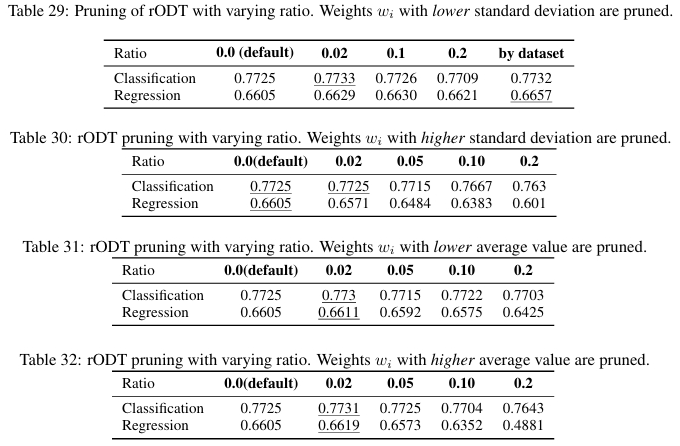
超参数分析

总体上，增加中间参数 \(m\)（从而增加条件数 \(N_{\text{cond}}\) 和 rODT数 \(N_{\text{rODT}}\)）和 rODT的深度 \(d\) 会提升模型性能，尤其是在大规模数据集上，模型能够从增加的容量中获益。


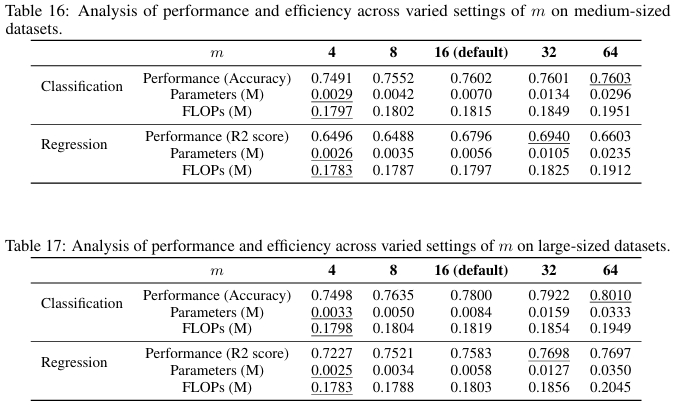
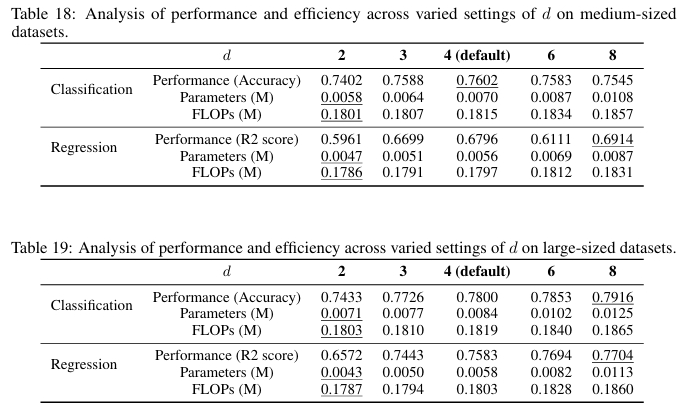
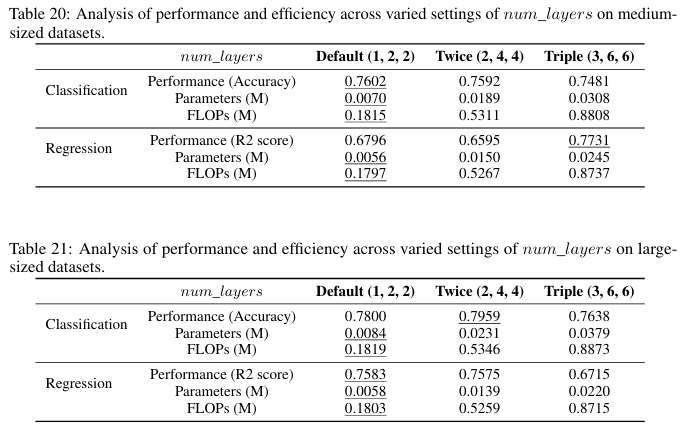
然而，简单地增加子网络 \(\Delta_{1}\), \(\Delta_{2}\), \(\Delta_{3}\) 的层数会导致参数量和FLOPs大幅增长，反而可能引起性能下降，这表明模型对深度的增加比较敏感，需要谨慎调整。

优点和创新点

个人认为，本文有如下一些优点和创新点可供参考学习：

1. DOFEN 模型通过“随机枚举条件+可微分权重学习”的两步法，成功将“开关式稀疏列选择”融入深度神经网络框架，克服了传统表格 DNN 只能进行稠密计算的局限。
2. DOFEN设计了“森林构建”与“森林聚合”两级集成，通过在 rODT 池上随机采样构建多个森林再进行预测聚合，等效于在深度学习模型中实现了高效的 Bagging，显著提升了模型稳定性并有效防止过拟合。