Paper Reading: Bivariate Decision Trees: Smaller, Interpretable, More Accurate

目录

Paper Reading 是从个人角度进行的一些总结分享，受到个人关注点的侧重和实力所限，可能有理解不到位的地方。具体的细节还需要以原文的内容为准，博客中的图表若未另外说明则均来自原文。

论文概况 详细
标题 《Bivariate Decision Trees: Smaller, Interpretable, More Accurate》
作者 Rasul Kairgeldin, Miguel Á. Carreira-Perpiñán
发表会议 ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD)（2024）
发表年份 2024
期刊等级 CCF-A
论文代码 文中未公开

作者单位：
University of California, Merced Merced, CA, USA

研究动机

决策树在统计机器学习中具有独特地位，与其他模型相比，决策树具有推理时间快、适合处理多类别问题​​、可解释性好等优点​​。但是决策树的缺点是预测准确性较低，这主要源于两个原因：

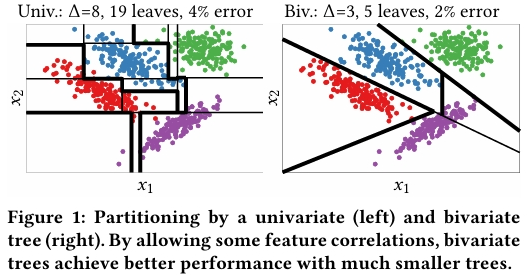
  1. 数据建模的不足​​：传统决策树每个决策节点仅基于单个输入特征进行操作，当特征存在相关性时，需要大量锯齿状分割来构建倾斜决策边界，导致树结构庞大、难以解释且泛化能力差。
  2. 优化策略的不足​​：优化树的损失函数是一个高度非凸问题，应用最广泛的贪心递归划分方法不优化树的全局目标函数，导致产生相当次优的树。

倾斜（多变量）决策树的倾斜分割无法通过枚举轻松优化（实际上是 NP 难问题），虽然已经提出了一些近似方法，但次优分割会产生下游级联效应，导致树结构庞大。由于每个分割现在使用所有特征，树变得笨重且难以解释。TAO（树交替优化）算法的出现使得能够有效训练单变量和（稀疏）倾斜树，与递归划分不同，TAO 在明确定义的参数树模型和目标函数上运行，在每次迭代中更新每个节点的参数以降低目标函数。研究表明，TAO 产生的单变量树比 CART、C4.5 等算法准确性更高，而倾斜树在准确性上显著超过单变量树。

文章贡献

本文提出了双变量决策树模型，通过限制每个决策节点最多使用两个特征，在保持可解释性的同时显著提升了传统决策树的表达能力。为了学习双变量决策树结构，本文提出了两种算法：基于贪心递归划分的快速算法（双变量 CART）；以及基于交替优化的较慢但更好的算法（双变量 TAO）。基于贪心递归划分的双变量 CART 算法实现了快速训练，基于交替优化的双变量 TAO 算法则通过全局目标函数优化产生更优树结构。模型采用特征成本正则化机制，允许节点自适应选择零变量（剪枝）、单变量或双变量分裂类型，其中双变量分裂通过线性组合两个特征有效捕捉特征交互效应，避免了单变量树需要复杂锯齿状分割逼近决策边界的问题，同时克服了多变量树因使用过多特征而丧失可解释性的缺陷。
image

本文方法

问题形式化与模型定义

考虑一个 K 类分类问题，数据集包含 N 个 D 维输入特征样本：\(\{(x_n, y_n)\}_{n=1}^N \subset R^D \times \{1,\ldots, K\}\)。树的结构为二元决策树，即每个决策节点恰好有 2 个子节点，节点集合包括：决策节点集合 \(\mathcal{N}_{dec}\)、叶子节点集合 \(\mathcal{N}_{leaf}\)、总节点集合 \(\mathcal{N} = \mathcal{N}_{dec} \cup \mathcal{N}_{leaf}\)。每个决策节点 \(i \in \mathcal{N}_{dec}\) 的路由函数定义为 \(f_i(x;\theta_i): R^D \rightarrow \{\text{left}_i, \text{right}_i\} \subset \mathcal{N}\)决策规则采用硬决策方式：如果 \(w_{ij}x_j + w_{ik}x_k + b_i < 0\)，则导向左子节点（\(\text{left}_i\)），否则导向右子节点（\(\text{right}_i\)）。
可学习参数为 \(\theta_i = \{w_i, b_i\}\)，关键约束是，\(\lVert w_i \rVert_0 \leq 2\)，确保每个节点最多使用两个特征。叶子节点包含恒定的标签分类器，输出单一类别 \(c_i \in \{1,\ldots, K\}\)。完整参数集合定义为：\(\Theta = \{(w_i, b_i)\}_{i \in \mathcal{N}_{dec}} \cup \{c_j\}_{j \in \mathcal{N}_{leaf}}\)。树的预测函数 \(T(x_n;\Theta)\) 引导样本 x 沿着从根节点到唯一叶子节点的路径，最终产生分类输出。
双变量树学习的核心在于正则化目标函数，基本目标函数的定义如下，其中 \(L(\cdot,\cdot)\) 是 0/1 损失函数，\(\lambda\) 是正则化超参数。
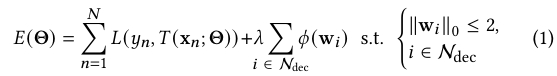
image
先前工作​​通常仅使用 L1 惩罚，虽然鼓励倾斜节点使用较少特征，但无法实现真正的双变量节点。本文引入了全新的正则化项\(\phi(w_i)\)，公式定义如下：
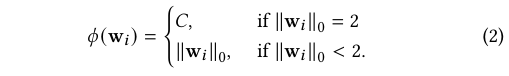
image
通过结合 L0 约束和新的 ϕ 惩罚项，该损失函数能够精确控制每个节点使用的特征数量（0、1 或 2 个）。当 \(\lVert w_i \rVert_0 = 0\) 时，节点将所有样本导向同一子节点，可被修剪，\(C > 1\) 确保双变量分割仅在能充分减少损失时被选择。这种正则化设计使得能够通过 λ 控制树中的节点数量，通过 C 控制树的单变量/双变量特性，从而实现"更准确、更小、更可解释"的双变量决策树。

Bivariate TAO

Bivariate TAO（Tree Alternating Optimization）是一种基于交替优化的双变量决策树训练算法。与传统的贪心递归划分方法（如 CART）不同，TAO 算法在给定的树结构上优化一个明确定义的目标函数，通过交替更新每个节点的参数来全局优化整个树模型。

定理支撑

TAO 算法基于可分离条件、简化问题两个关键定理。可分离条件是决策树的目标函数可以在​​非后代节点​​之间实现完全分离和独立优化，这是由于树结构的硬决策特性所决定的。对于任意两个非后代节点 i和 j（即不存在父子关系的节点），它们的简化集满足：\(\mathcal{R}_i \cap \mathcal{R}_j = \emptyset\)。可分离条件的优势在于：

  1. 可以令位于同一深度的节点可以同时进行优化，从而提高计算效率；
  2. 具有局部独立性，优化某个节点时只需考虑到达该节点的样本子集，而不需要关注整个数据集；
  3. 每个节点的优化问题可以独立求解，简化了算法设计。

简化问题定理指出，在固定其他节点参数的情况下，优化单个节点 \(i \in \mathcal{N}\) 的参数可以转化为一个定义明确且相对简单的优化问题，该问题仅涉及该节点的简化集 \(\mathcal{R}_i\)。

  • 对于叶子节点 \(i \in \mathcal{N}_{\text{leaf}}\)，优化问题简化为：\(c_i = \operatorname{argmax}_{k \in \{1,\ldots,K\}} \sum_{n \in \mathcal{R}_i} L(y_n, k)\)，解决方案是选择简化集中样本的多数类作为叶子节点的预测标签。
  • 对于决策节点 \(i \in \mathcal{N}_{\text{dec}}\)，优化问题转化为0/1损失的二元分类问题，如下公式所示。其中 \(\bar{y}_n \in \{\text{left}, \text{right}\}\) 是伪标签，表示将样本 \(x_n\) 发送到哪个子节点能够产生更低的损失值。

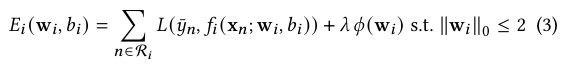
image
简化问题的实际求解机制基于伪标签的生成，伪标签生成过程如下：

  1. 前向传播：将简化集 \(\mathcal{R}_i\) 中的每个样本分别发送到左右子节点
  2. 损失计算：对于每个样本，计算发送到左右子节点后产生的损失值
  3. 伪标签分配：选择产生较低损失的子节点方向作为该样本的伪标签

通过伪标签的引入，复杂的树结构优化问题被分解为一系列相对简单的二元分类问题，每个问题只涉及单个决策节点的参数优化。通过两个定理的协同作用，决策树基于深度优先的反向优化机制，从最深层节点开始，逐步向根节点推进。同一深度的节点可以并行处理，每个节点的局部优化都贡献于全局目标函数的下降。

决策节点的三种分裂方案

Bivariate TAO 算法中，决策节点的分裂方案基于对简化问题(3)的优化求解。算法为每个决策节点提供三种不同类型的分裂方案，通过权衡分裂质量和模型复杂度来选择最优方案。
方案一为双变量分裂（Bivariate Split），该解法对每对特征预设一组方向向量（均匀采样于 0°–180°），将样本投影到每个方向后寻找最优阈值。其约束条件为 \(\|w_i\|_0 = 2\)，即使用两个特征，正则化成本为 \(\lambda C\)（其中\(C > 1\)），数学形式为：\(w_{ij}x_j + w_{ik}x_k + b_i < 0\)。
该方法需要遍历所有 \(\binom{D}{2}\) 个特征组合，在二维空间中均匀采样 H 个方向向量 \(w_l \in W\)，将选定特征对投影到每个方向，寻找最优阈值。方案一的计算复杂度为：\(O(D^2 \Delta |\mathcal{R}_i|^2) + \Theta(D^2 |\mathcal{R}_i|^2 \log |\mathcal{R}_i|)\)，计算过程如下：

for 每个特征对(j,k):
    for 每个方向w_l:
        x_proj = 投影样本到w_l方向
        b_optimal = 寻找最优阈值(x_proj)
        计算当前配置的损失值
    end for
end for
选择损失最小的配置作为最终解

该方案的样例如下图所示：
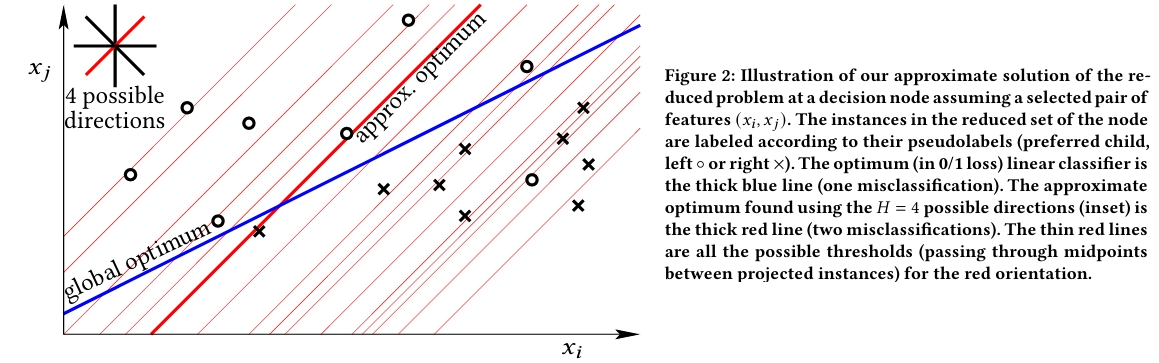
screenshot-1761559890218

方案二为单变量分裂（Univariate Split），该解法与传统 CART 类似，对每个特征枚举最优阈值。该方法的约束条件为\(\|w_i\|_0 = 1\)（使用一个特征），正则化成本为 \(\lambda\)，数学形式：\(w_{ij}x_j + b_i < 0\)（等价于\(x_j < \text{threshold}\)）。该方法采用经典的阈值优化策略，对每个特征的样本值进行排序，然后考虑相邻样本值的中点作为候选阈值计算每个候选阈值对应的分类损失，最后选择使损失最小的特征和阈值组合。该方法计算复杂度为 \(O(D \Delta |\mathcal{R}_i|) + \Theta(D |\mathcal{R}_i| \log |\mathcal{R}_i|)\)。
方案三为零变量分裂（Zero-variate Split），该解法中节点将所有样本路由到同一侧，相当于剪枝该节点。该方法的约束条件为 \(\|w_i\|_0 = 0\)，即不使用任何特征，正则化成本为 \(0\)，数学形式为 \(b_i < 0\)，表示所有样本被路由到同一子节点。求解方法是极其简单的二选一决策，左子树路由为 \(b_i = -1\)，表示所有样本发送到左子节点；右子树路由为 \(b_i = +1\)，所有样本发送到右子节点；通过损失比较选择路由方向使得总体损失更小。零变量分裂意味着该决策节点实际上是冗余的，因为它的存在不影响样本的路经选择，这类节点在算法后期会被剪枝移除。
算法基于正则化后的总损失进行方案选择，如下公式所示。当多个方案损失相同时，优先选择参数更少的方案（零变量 > 单变量 > 双变量）。参数\(C\)和$\lambda共同控制方案选择，小 \(\lambda\) 大 \(C\) 导致倾向双变量分裂，大 \(\lambda\) 小 \(C\) 导致倾向简单分裂或剪枝。
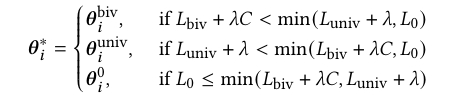
image
该部分的伪代码如下图所示：
ScreenShot_2025-10-27_181318_817

回归任务

Bivariate TAO 算法从分类任务扩展到回归任务时，需要进行两个关键修改。第一方面是叶子节点预测值，在分类任务中叶子节点采用多数投票原则，在回归任务中预测值改为简化集中样本目标值的均值：

\[\hat{y}_i = \frac{1}{|\mathcal{R}_i|} \sum_{n \in \mathcal{R}_i} y_n \]

第二方面是决策节点目标函数，分类任务中的决策节点的简化问题转化为 0/1 损失的二元分类问题，在回归任务中目标函数需要改为基于加权二元分类的形式。对于每个样本，分别计算将其发送到左右子树后产生的回归损失，左子树损失为 \(L_{\text{left}} = L(y_n, T_{\text{left}}(x_n))\)，右子树损失为 \(L_{\text{right}} = L(y_n, T_{\text{right}}(x_n))\)。根据子树损失大小分配样本到不同方向的"偏好权重"，如此将决策节点的优化目标变为最小化加权分类错误。偏好权重的公式如下，这种权重计算方式确保了损失较小的子树获得更高的样本分配权重。

\[w_n = \frac{\exp(-L_{\text{left}})}{\exp(-L_{\text{left}}) + \exp(-L_{\text{right}})} \]

回归形式的 TAO 算法优化以下目标函数，其中 \(L_{\text{reg}}\) 是回归损失函数，常用的包括平方损失（\(L(y, \hat{y}) = (y - \hat{y})^2\)）、绝对损失（\(L(y, \hat{y}) = |y - \hat{y}|\)）。

\[E(\Theta) = \sum_{n=1}^{N} L_{\text{reg}}(y_n, T(x_n; \Theta)) + \lambda \sum_{i \in \mathcal{N}_{\text{dec}}} \phi(w_i) \]

正则化路径

正则化路径是 TAO 算法中用于控制模型复杂度和选择最优树结构的机制，它通过系统性地调整正则化参数 λ 的取值，探索从最简单到最复杂的模型空间。
对于 K 类分类问题，设各类样本数为 \(N_1 \geq N_2 \geq \cdots \geq N_K\)，其中 \(N_1\) 为最大类的样本数。λ 的理论取值范围为 \(\lambda \in \{0, 1, \ldots, N - N_1\}\)，当\(\lambda \geq N - N_1\)时，最优树将退化为单叶子节点，预测值为最大类的标签。这是因为正则化项的惩罚已经超过了任何分裂可能带来的收益。
正则化项 \(\lambda\phi(w_i)\) 可以理解为允许的最大误分类样本数，当某个决策节点的分裂带来的误差减少量小于\(\lambda\phi(w_i)\)时，该节点将被剪枝。由于 0/1 损失函数取整数值，正则化路径只需要在有限的 λ 值上进行计算，大大减少了计算复杂度。计算过程为：

  1. 计算当前节点的最小损失差异：\(\Delta L_{\min} = \min(L_0 - L_{\text{biv}}, L_0 - L_{\text{univ}})\)；
  2. 确定下一个关键 λ 值：\(\lambda_{\text{next}} = \lambda_{\text{current}} + \Delta L_{\min}\)；
  3. 只在 λ 值发生实际变化的点进行完整优化。

回归任务中损失函数取连续值，需要调整正则化路径的计算策略。需要采用等间距或对数间距的 λ 值网格搜索，基于损失函数曲率动态调整搜索密度，还需要对连续损失变化的收敛标准进行设定。

bivariate CART

Bivariate CART 是基于传统 CART 算法的快速双变量决策树学习算法。与完全优化的 Bivariate TAO 不同，Bivariate CART 采用贪心递归划分策略，通过特定的特征工程技巧实现双变量分裂。
bivariate CART 有两种实现方式。方式一是修改 CART 分裂步骤，该方法比较高效，它直接修改 CART 的分裂评估函数，使其能够评估双变量分裂的质量。具体而言为：遍历所有 \(\binom{D}{2}\) 个特征组合，然后在每个特征对的二维空间中采样 H 个方向，使用 Gini 指数或信息增益评估每个候选分裂，选择评估指标最优的双变量分裂。
方式二是使用特征增强方法，该方法内存消耗较大，它通过预处理构造增强特征集，然后运行标准单变量 CART。工作流程为：首先创建包含原始特征和双变量组合的增强特征集，新特征集大小为\(D + \binom{D}{2} \times |H|\)，然后在增强特征集上执行传统单变量 CART。
Bivariate CART 的时间复杂度与单变量 CART 同数量级，远低于 Bivariate TAO。Bivariate CART 基于现有 CART 即可实现，只需添加预处理或分裂搜索扩展，可扩展性较强。

正则化参数的相互作用

正则化参数 λ 控制着模型复杂度与训练误差之间的基本权衡关系。当 λ 取值较小时，算法优先考虑降低训练误差，倾向于生成结构更复杂的树；而当 λ 增大到临界值 λ* 时，正则化项的惩罚超过任何分裂可能带来的收益，导致树结构退化为单一的叶子节点。特征成本参数 C 则决定了不同类型分裂的相对成本，当 C≤1 时双变量分裂成本不高于单变量分裂，算法会偏好使用双变量节点；当 C 增大到临界值 C* 时，单变量分裂成为主导选择。
基于参数空间的划分，可以用相位图展现出三个特征鲜明的区域：

  1. 零变量主导区域（λ ≥ λ*）：树结构完全剪枝，所有样本被预测为最大类的标签；
  2. 在双变量主导区域（C ≤ 1 且 λ < λ*）：所有决策节点都采用双变量分裂，充分利用特征间的交互效应；
  3. 在单变量主导区域（C ≥ C* 且 λ < λ*），算法倾向于选择结构更简单的单变量分裂。

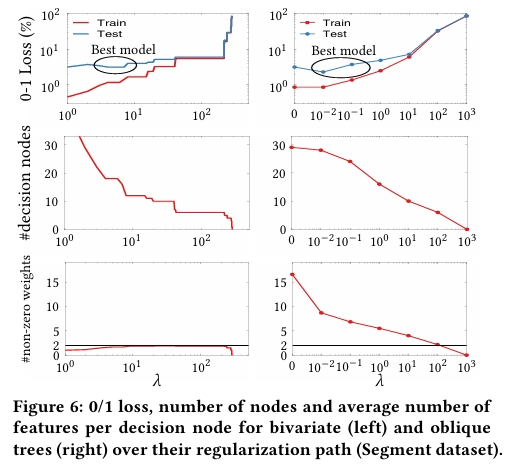
image
图中椭圆标识出的最佳性能区域表明，最优模型通常出现在混合区域（0<λ≤λ 且 1<C≤C）内，该区域内的树结构能够自适应地选择分裂类型，平衡模型复杂度和表达能力。基于这一发现，论文将 C 固定在 [1.1,1.5] 范围内（略微偏好双变量分裂），再通过交叉验证选择 λ，从而在保证性能的同时显著降低调优复杂度。

实验结果

数据集和实验设置

实验采用了多个 UCI 数据集，涵盖了不同规模、类型和难度的分类与回归任务。对于没有独立测试集的数据集，采用随机抽样策略将 20% 的样本留作测试集，另外 10% 作为验证集用于超参数调优，剩余 70% 用于模型训练。所有实验均重复 3 次并报告平均值和标准差。对比算法方面，单变量决策树​​方面包括经典的 CART 算法、C5.0算法（RuleQuest的C语言实现）；​​双变量决策树​​方面对比了本文提出的Bivariate CART 和 Bivariate TAO，以及现有的 BiDT 算法；​​多变量决策树​​方面包含了稀疏倾斜树作为参照。

分类和回归任务评估

实验结果显示，双变量 TAO 树在几乎所有测试数据集上都表现出色，不仅测试准确率显著高于单变量树（通常提升 2-5 个百分点），而且树结构更加紧凑。
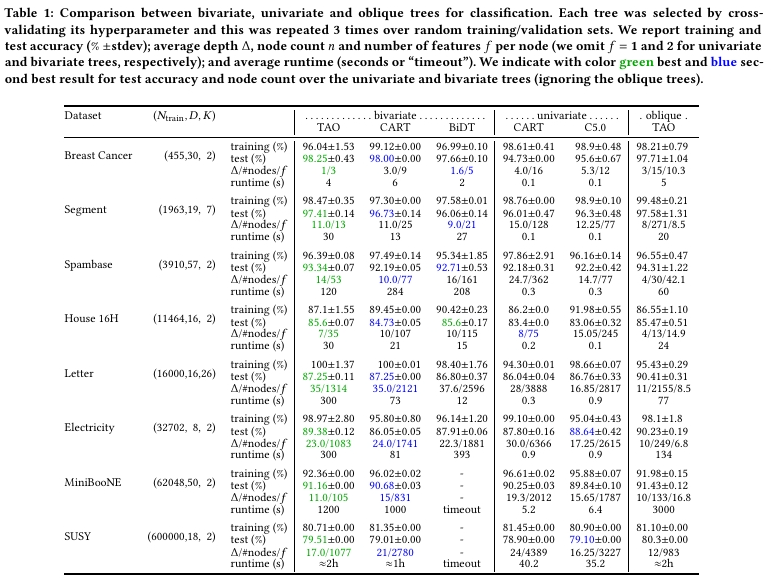
image
在回归任务中，双变量树同样在 RMSE 指标上明显优于传统方法。
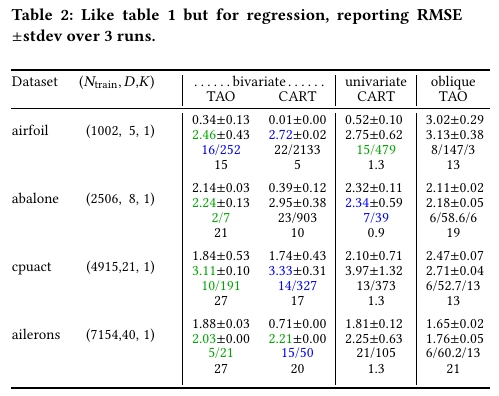
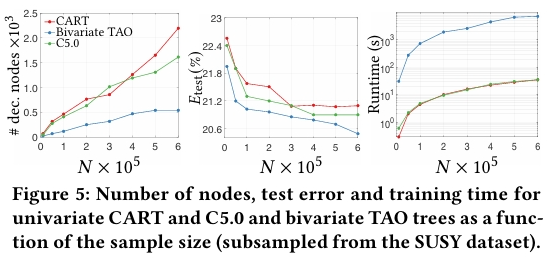
image

样本量分析

在样本量敏感性分析方面，传统单变量树会随样本量增加持续增长复杂度，即使准确率已趋于稳定；双变量 TAO 树能在达到足够性能后自动停止增长，体现了更好的优化特性。
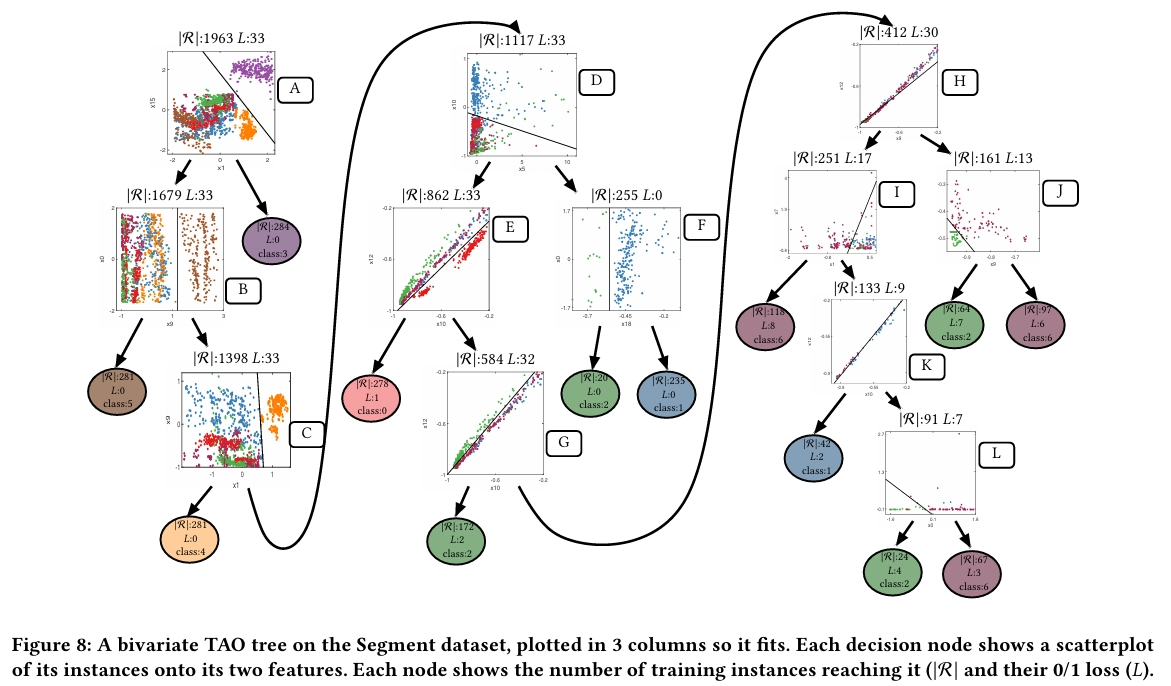
image

可解释分析

在 Breast Cancer UCI 数据集中，双变量 TAO 树仅用深度 3 和 5 个叶子节点就实现了 2% 错误率，而单变量 CART 树需要深度 7 和 16 个叶子节点且错误率达 6.4%。双变量树自动选择了 6 个关键特征，生成的 5 条 IF-THEN-ELSE 规则简洁明了。
image
Segment 的每个决策节点的二维散点图投影清晰显示了不同类别的分离模式，如节点 E 中类别 0 的聚类结构和节点 G 中的线性模式。树结构呈现明显的不对称性，多数类别在浅层节点即被有效分离，仅复杂类别需要更深层处理。
image

正则化路径分析

实验详细比较了双变量树与稀疏倾斜树在正则化路径上的行为差异。结果显示，稀疏倾斜树仅在极大正则化强度 \(\lambda\) 下才达到平均 2 个特征的使用水平，此时模型性能已严重退化；双变量树在整个正则化路径上都能保持平均特征数 \(\leq 2\)，同时在最佳性能点达到与倾斜树相近的准确率但使用特征数显著更少。
image

优点和创新点

个人认为，本文有如下一些优点和创新点可供参考学习：

  1. 通过限制节点最多使用两个特征，在保持可解释性的同时显著提升了模型表达能力，解决了传统单变量树无法捕捉特征交互的固有缺陷。
  2. 提出 Bivariate CART 和 Bivariate TAO 双路径训练方案，分别满足效率与精度的不同需求，其中 TAO 的交替优化框架保证了全局收敛性。
  3. 引入特征成本正则化项，使节点能根据数据特性自适应选择零变量（剪枝）、单变量或双变量分裂，实现真正的结构学习。
posted @ 2025-10-28 16:12  乌漆WhiteMoon  阅读(6)  评论(0)    收藏  举报