Paper Reading: Vanilla Gradient Descent for Oblique Decision Trees

目录

• 研究动机
• 文章贡献
• 本文方法
  • DTSemNet 结构
  • 模型结构样例
  • 语义等价性定理及其证明
  • 具体任务的实现
• 实验结果
  • 分类性能比较
  • 回归性能比较
  • 强化学习性能比较
  • 敏感性分析
• 优点和创新点

Paper Reading 是从个人角度进行的一些总结分享，受到个人关注点的侧重和实力所限，可能有理解不到位的地方。具体的细节还需要以原文的内容为准，博客中的图表若未另外说明则均来自原文。

论文概况	详细
标题	《Vanilla Gradient Descent for Oblique Decision Trees》
作者	Subrat Prasad Panda, Blaise Genest, Arvind Easwaran, Ponnuthurai Nagaratnam Suganthan
发表会议	European Conference on Artificial Intelligence (ECAI)（2024）
发表年份	2024
会议等级	CCF-B
论文代码	https://github.com/CPS-research-group/dtsemnet.

作者单位：

1. NTU, Singapore
2. CNRS, IPAL, France and CNRS@CREATE, Singapore
3. KINDI Computing Research, Qatar University, Qatar

研究动机

决策树（DTs）作为高度非线性的机器学习模型，在表格数据等领域表现出色。然而学习准确的决策树，特别是斜决策树时经常存在组合爆炸问题，即在每个节点选择最优分裂点导致计算复杂度呈指数级增长。同时现有的方法需要大量计算资源，导致训练时间过长，以及倾斜决策树在回归任务中普遍存在泛化能力不足的问题。当前决策树学习方法可分为四类：

方法类型	代表算法	优势	局限性
贪心优化	CART	简单快速	通常学习性能较差的树
非贪心优化	TAO	全局目标优化	计算成本仍高于基于梯度的方法
全局搜索	MIP, EA	能找到较优解	在树结构复杂时计算不可行
梯度下降	软决策树	训练效率高	只能产生概率性决策

为了在 DT 的训练阶段应用梯度下降，大多数先前工作采用“软”决策来实现。但是基于 Sigmoid 等激活函数的软决策树只能提供概率性决策，将其硬化为硬决策树会导致显著的精度损失。同时梯度近似方法也存在缺陷，如 DGT 和 ICCT 等方法使用 Straight-Through Estimators（STEs）进行梯度近似，这种近似在大型数据集或强化学习环境中会产生误差累积，影响训练效果。

文章贡献

本文提出了 DTSemNet 模型，该架构通过四层神经网络结构实现了与斜决策树的语义等价映射。它使用 ReLU 激活函数和线性运算使其可微，并允许梯度下降应用于学习结构，同时在语义上等同于倾斜决策树的架构，使得 DT 中的决策节点与 NN 中的可训练权重一一对应。DTSemNet 的模型结构为：输入层接收特征向量，第一隐藏层作为决策层使用线性激活函数学习内部节点的参数，第二隐藏层通过 ReLU 激活函数和固定权重实现硬决策路径的激活，输出层则基于预定义的树拓扑结构通过固定连接规则编码叶子节点选择逻辑。DTSemNet 首次实现了无需梯度近似即可通过标准梯度下降直接学习硬决策树的方法，在分类任务中避免 Straight-Through Estimator（STE）的使用，在回归任务中仅需单次 STE 近似。实验证明其在监督学习和强化学习环境中显著提升了训练效率和准确性，为可解释机器学习提供了新的技术路径。

本文方法

DTSemNet 结构

对于一棵非叶节点的决策函数表示为“A·x + b > 0 ?”的倾斜决策树，DTSemNet 能够将其语义等价地编码为神经网络。它采用四层前馈神经网络结构，与决策树的组件的对应关系和功能如下表所示：

层次	对应决策树	功能
输入层	输入​​	接收特征向量和偏置项
第一隐藏层	决策	对应决策树的内部节点，包含可训练参数
第二隐藏层	路径激活	使用 ReLU 激活函数实现硬决策逻辑
输出层	叶子	对应决策树的叶子节点

输入层由 n+1 个节点构成，其中 n 为特征维度，用于输入 n 个特征 x₁, x₂, ..., xₙ；以及 1 个常量值为 1 的偏置单元，为决策函数的截距项。数学表示为 X = [x₁, x₂, ..., xₙ, 1]ᵀ。第一隐藏层/决策层与输入层全连接，包含 k 个节点 I₁, I₂, ..., Iₖ，对应决策树的 k 个内部节点。该层次的可训练参数包括权重矩阵 A∈R^{k×n} 和偏置向量 b∈Rᵏ，分别对应决策树的斜分裂参数和截距项。激活函数第一隐藏层的线性激活，其计算过程表示为：valueₓ(I) = A·x + b。第二隐藏层/路径激活层用于实现硬决策逻辑，确保每个决策只有一条路径被激活。该层次使用的激活函数为 ReLU 函数，包含 2k 个节点，每个决策节点对应两个路径节点：

• ⊤ᵢ：代表决策 Dᵢ 为真，Iᵢ 到 ⊤ᵢ 的权重为 +1；
• ⊥ᵢ：代表决策 -Dᵢ 为真，Iᵢ 到 ⊥ᵢ 的权重为 -1。

输出层/叶子节点层包括 m 个叶子节点 L₁, L₂, ..., Lₘ，它的连接规则是基于决策树拓扑结构的固定权重编码，权重取值于{0, 1}。权重值由以下三条规则决定：

• 右子树：若叶子 Tⱼ 在节点 Tᵢ 的右子树中，则 Lⱼ 从 ⊤ᵢ 接收输入（权重 1）；
• 左子树：若叶子 Tⱼ 在节点 Tᵢ 的左子树中，则 Lⱼ 从 ⊥ᵢ 接收输入（权重 1）；
• 无关节点：若叶子 Tⱼ 不经过节点 Tᵢ，则 Lⱼ 从 ⊤ᵢ 和 ⊥ᵢ 都接收输入（权重均为 1）。

DTSemNet 通过以下定理确保神经网络输出与决策树决策完全一致：对于任意输入 x，argmaxⱼ(valueₓ(Lⱼ)) = Lᵢ，当且仅当叶子 Tᵢ 的所有关联决策在 x 下为真。当输入一个样本 x 时，DTSemNet 按照以下流程工作：

1. 前向传播：决策层计算 Aᵢx + bᵢ，路径激活层通过 ReLU 得到每个决策的真/假激活值。
2. 叶子节点值计算：每个叶子节点 Lⱼ 的值是其所有输入连接的值之和。
3. 正确叶子胜出：对于被树选中的叶子 T_ℓ，其路径上所有决策的激活值都为正，且通过规则 1 和 2 被正确接收。同时，无关决策（规则 3）也贡献正值。因此，value(L_ℓ) 是所有路径激活值之和，达到最大值。对于任何其他叶子 Tⱼ，其路径上至少有一个决策与 x 的真实路径冲突，导致它无法从该决策获得激活值（输入为0），因此 value(Lⱼ) < value(L_ℓ)。
4. 输出：对输出层进行 argmax 操作，值最大的 L_ℓ 即对应被选中的叶子。

模型结构样例

下图展示了一个 DTSemNet 的模型结构样例，以及和等价的倾斜决策树结构：

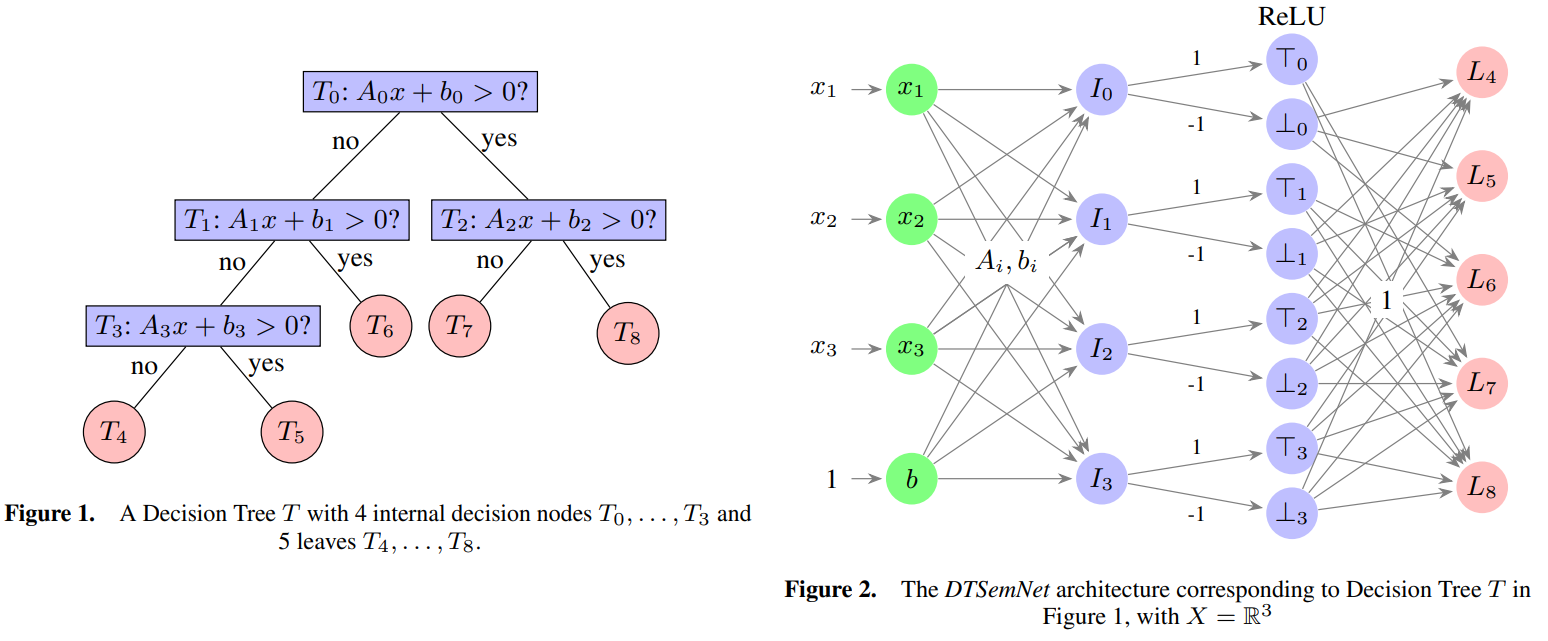
该样例的 DTSemNet 不同层次与倾斜决策树的组件的对应关系如下：

DTSemNet 层	对应决策树组件	说明
输入层	特征空间	输入特征 x₁, x₂, x₃ 和偏置单元 b
第一隐藏层（决策层）	内部节点 T₁, T₂, T₃	节点 I₁, I₂, I₃ 分别对应树中的 T₁, T₂, T₃，可训练权重直接对应决策参数 Aᵢ 和 bᵢ，根节点 T₀ 的决策被隐含处理
第二隐藏层（路径激活层）	决策的真/假分支	每个决策节点 Iᵢ 扩展出两个节点：⊤ᵢ（决策为真）和 ⊥ᵢ（决策为假），使用 ReLU 激活函数实现硬决策
输出层（叶子层）	叶子节点 T₄ 至 T₈	节点 L₄, L₅, L₆, L₇, L₈ 分别对应树的叶子节点，其值的大小决定了哪个叶子被选中

对于路径编码，以叶子结点 T₄ 为例，到达叶子节点 T₄ 的唯一路径为：

1. 从根节点 T₀，选择左分支（决策 D₀ 为假，记为 -D₀）；
2. 到达节点 T₁，选择左分支（决策 D₁ 为假，记为 -D₁）；
3. 到达节点 T₃，选择左分支（决策 D₃ 为假，记为 -D₃）；
4. 到达叶子节点 T₄，关联决策序列为：-D₀, -D₁, -D₃。

根据 L₄ 的路径，得到其连接权重如下表所示：

决策节点	T₄ 的路径关系	应用规则	L₄ 的连接权重设置
D₀	在 T₀ 的左子树中	规则 2	从 ⊥₀ 输入（权重 1），从 ⊤₀ 输入（权重 0）
D₁	在 T₁ 的左子树中	规则 2	从 ⊥₁ 输入（权重 1），从 ⊤₁ 输入（权重 0）
D₂	路径不经过T₂	规则 3	从 ⊤₂ 和 ⊥₂ 输入（权重均为 1）
D₃	在 T₃ 的左子树中	规则 2	从 ⊥₃ 输入（权重 1），从 ⊤₃ 输入（权重 0）

规则 3 通过为所有叶子节点提供统一的“基础分”，确保比较的公平性。对于 L₄ 而言，这个基础分来自于决策 D₂ 的信息量：valueₓ(⊤₂) + valueₓ(⊥₂)。当输入 x 使得路径 [-D₀, -D₁, -D₃] 成立时，L₄ 从其路径上的三个相关决策（D₀, D₁, D₃）和无关决策（D₂）都获得全额贡献：valueₓ(L₄) = valueₓ(⊥₀) + valueₓ(⊥₁) + [valueₓ(⊤₂) + valueₓ(⊥₂)] + valueₓ(⊥₃)。
其他叶子节点由于路径冲突，至少缺失一个决策的贡献值。例如 L₅ 的路径要求 D₃ 为真，但当前输入下 D₃ 为假，因此 L₅ 无法从 ⊤₃ 获得贡献（值为 0），导致其总值严格小于 L₄：valueₓ(L₅) = valueₓ(L₄) - valueₓ(⊤₃) [当 D₃ 为假时]。由于 valueₓ(⊤₃) > 0，严格保证 valueₓ(L₅) < valueₓ(L₄)，从而确保 L₄ 的值严格最大。

语义等价性定理及其证明

定理 1（语义等价性）：考虑将 DTSemNet 作为分类器，使用标准的 argmax 操作选择具有最高值的输出类，其决策与原始决策树完全一致。即对于所有输入向量 x∈X，有：

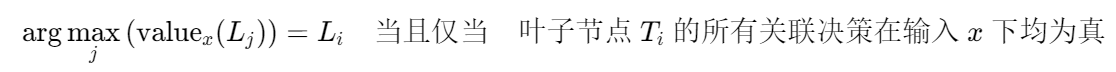
证明基于以下重要观察：

1. 对于任何输入 x∈X，有且仅有一个叶子节点 Tᵢ 的所有关联决策都为真；
2. 对于其他任何叶子节点 Tⱼ(j≠i)，至少存在一个关联决策在 x 下为假；
3. 由于 ReLU 函数的性质，对于每个决策节点对(⊥ᵢ, ⊤ᵢ)，恰好有一个输出为正，另一个为 0。
   ​

• 正向证明：假设 argmaxⱼ(valueₓ(Lⱼ))=Lᵢ，需要证明叶子节点 Tᵢ 的所有关联决策在输入 x 下均为真。采用反证法：假设存在某个与 Tᵢ 关联的决策 Dₖ 在 x 下为假，根据 DTSemNet 架构，这将导致 Lᵢ 无法从相应的 ⊤ₖ 或 ⊥ₖ 节点获得完整的贡献值，从而存在另一个叶子节点 Tⱼ 的路径与x的真实决策路径更匹配，使得 valueₓ(Lⱼ)>valueₓ(Lᵢ)，与最大值的假设矛盾。
• 反向证明：假设叶子节点 Tᵢ 的所有关联决策在输入x下均为真，需要证明 argmaxⱼ​(valueₓ(Lⱼ))=Lᵢ。首先计算正确叶子节点的值：
  
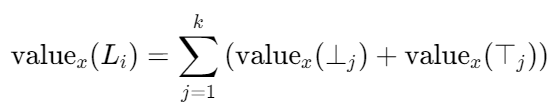
  对于任何其他叶子节点 Tⱼ(j≠i)，由于至少存在一个决策 Dₘ 的评估结果与 Tⱼ 路径要求相反，设 D^xₘ 是 Tⱼ 路径上与x实际决策相冲突的决策。此时 valueₓ(⊤ₘ)=0，且根据路径编码规则，Tⱼ 需要从 ⊤ₘ 获得输入但实际获得值为 0，因此：
  
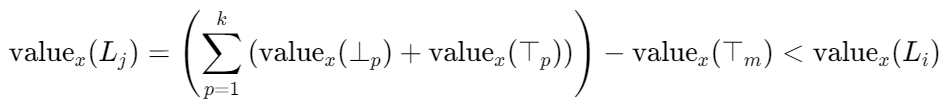
  由于 valueₓ(⊤ₘ)>0，不等式严格成立。

具体任务的实现

在多分类任务的实现方面，令让 T_class 为平衡决策树，每个类对应一个叶子。一个样例如下图所示，包括 left、right、balanced 3 个类别，其对应的叶子结点按照实例的比例进行平衡。DTSemNet 的分类版本在基础架构上扩展了类别聚合层，通过将决策树的叶子节点映射到具体的类别标签实现分类。聚合层的每个类别对应一个输出节点 \(C_1, \ldots, C_\ell\)，如果叶子 \(T_j\) 属于类别 \(\alpha_i\)，则从叶子节点 \(L_j\) 到类别节点 \(C_i\) 的权重为 1，反之为 0。在每个类别节点上执行 MaxPool，选择关联叶子中的最大输出值。

在回归任务的实现方面，DTSemNet 在每个叶子节点关联一个线性回归器来实现。回归模型的扩展包括回归器层和选择机制。每个叶子节点 \(T_j\) 关联线性参数向量 \(\theta_j \in \mathbb{R}^n\) 和偏置 \(\alpha_j \in \mathbb{R}\)，最终输出为选中叶子对应回归器的值 \(\theta_\ell \cdot x + \alpha_\ell\)。由于 argmax 操作的不可微性，回归模型在输出层使用 Straight-Through Estimator（STE）进行梯度近似。相比其他现有工作，DTSemNet 仅在输出层使用一次 STE 近似，大大减少了近似误差。

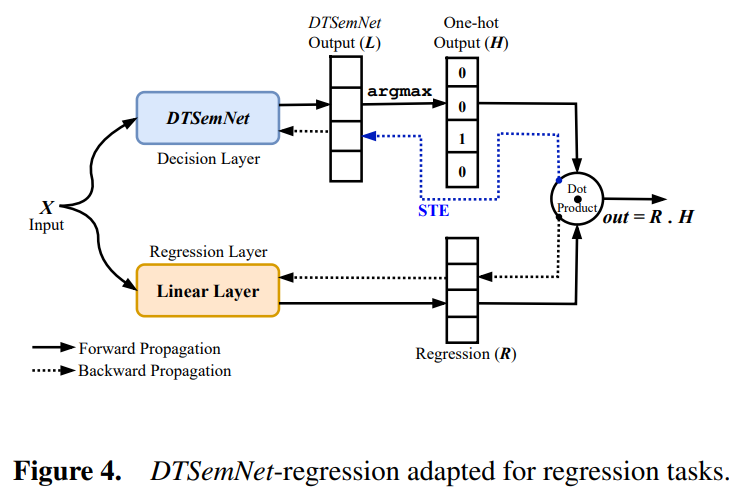
在强化学习的实现方面，可以用 DTSemNet 架构替代传统神经网络策略函数。对于离散动作空间任务，DTSemNet 的分类变体可以直接用作策略网络，每个动作对应决策树的一个叶子节点，通过 argmax 操作选择具有最高值的动作。对于连续动作空间任务，DTSemNet 的回归变体可以用于学习确定性策略或动作价值函数，每个叶子节点关联一个多维回归器，输出连续动作向量。

实验结果

分类性能比较

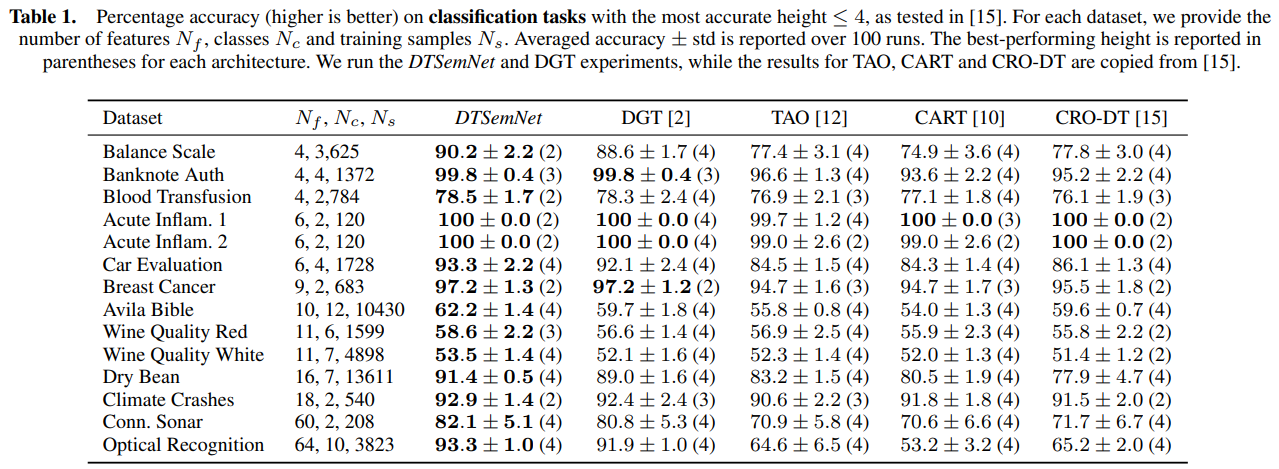
在 14 个分类数据集上对比了分类性能，结果如下表所示，可见 DTSemNet 在小型决策树（deeth ≤ 4）的设置下性能优于现有方法。

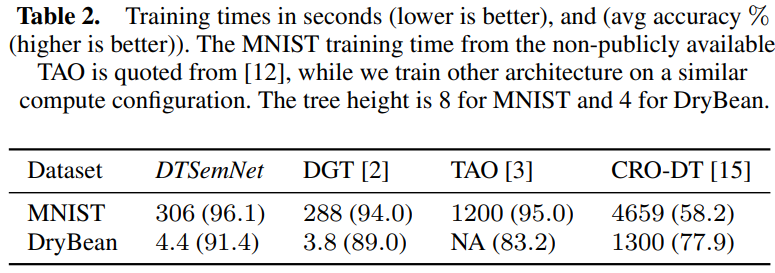
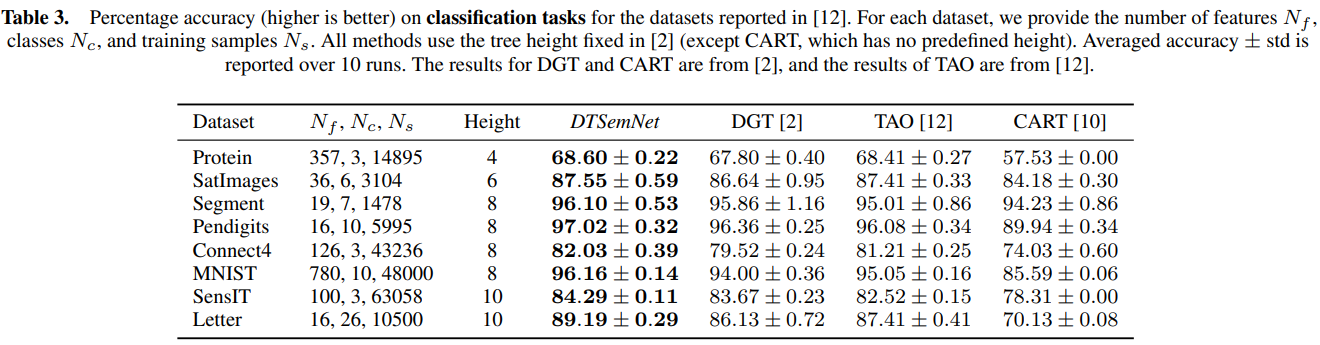
较深的决策树（deepth ≥ 8）的实验如下表所示，结果进一步验证了 DTSemNet 的可扩展性。在 MNIST 数据集上，DTSemNet 和 DGT 的训练时间约为 TAO 的 1/10，CRO-DT 的1/50，说明其训练效率高。

回归性能比较

在 7 个回归数据集上，将 DTSemNet 和带有回归器叶子节点的方法比较，结果如下表所示，可见 DTSemNet 在 4 个数据集上表现最佳，在其余 3 个数据集上仅次于 TAO-linear。回归性能的差异主要源于梯度近似策略的不同，DTSemNet 仅在输出层使用一次 STE 近似，而对比方法需要在每个决策节点进行近似带来了累积误差。

强化学习性能比较

强化学习实验包括了 4 个离散动作环境和 2 个连续动作环境。在离散动作任务中 DTSemNet 的性能最优，连续动作任务中 DTSemNet 与其他神经网络策略性能相当，同时其具备可解释的决策过程。

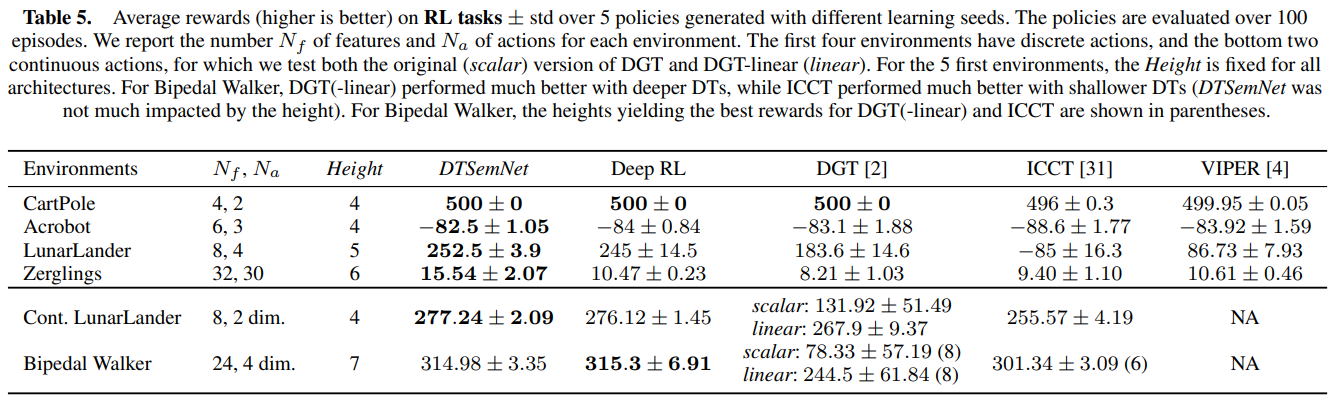
敏感性分析

使用不同深度的 DTSemNet 模型进行实验，验证其对树深度选择的鲁棒性。与 ICCT 和 DGT 等方法在不同深度下表现不稳定相比，DTSemNet 在深度 6-8 范围内保持一致的性能水平。

优点和创新点

个人认为，本文有如下一些优点和创新点可供参考学习：

1. 本文首次将硬斜决策树通过可逆编码映射为神经网络结构，实现决策树与神经网络的严格语义等价，为梯度下降直接优化决策树奠定了理论基础；
2. 模型设计中尽量减少了 STE 等梯度近似方法的使用，支持使用标准梯度下降进行训练，显著提升了优化精度和训练稳定性；
3. DTSemNet 支持分类、回归及强化学习任务，在离散与连续动作空间均达到与神经网络相当的绩效；
4. 模型具有决策树的可解释性，同时具备较高的准确率和训练效率。