Paper Reading: MDGP-forest: A novel deep forest for multi-class imbalanced learning based on multi-class disassembly and feature construction enhanced by genetic programming

目录

• 研究动机
• 文章贡献
• 本文方法
  • MDGP-Forest框架
  • 多类降解与重采样
  • 类相关的 GP 特征构造
• 实验结果
  • 数据集和实验设置
  • 对比实验
  • 消融实验
  • 调参实验
  • 运行时间
• 创新点

Paper Reading 是从个人角度进行的一些总结分享，受到个人关注点的侧重和实力所限，可能有理解不到位的地方。具体的细节还需要以原文的内容为准，博客中的图表若未另外说明则均来自原文。

论文概况	详细
标题	《MDGP-forest: A novel deep forest for multi-class imbalanced learning based on multi-class disassembly and feature construction enhanced by genetic programming》
作者	Zhikai Lin, Yong Xu, Kunhong Liu, Liyan Chen
发表期刊	Pattern Recognition
发表年份	2026
期刊等级	中科院 SCI 期刊分区(2025年3月最新升级版）1 区，CCF-B
论文代码	https://github.com/MLDMXM2017/MDGP-Forest

作者单位：

1. Department of Digital Media Technology, School of Film, Xiamen University, Xiamen, Fujian Province 361005, China
2. Xiamen Key Laboratory of Intelligent Fishery, Xiamen Ocean Vocational College, Xiamen, 361100, China
3. Key laboratory of Digital Protection and Intelligent Processing of lntangible Cultural Heritage of Fujian and Taiwan, Ministry of Culture and Tourism
4. Xiamen Key Laboratory of Intelligent Storage and Computing, School of Informatics, Xiamen University

研究动机

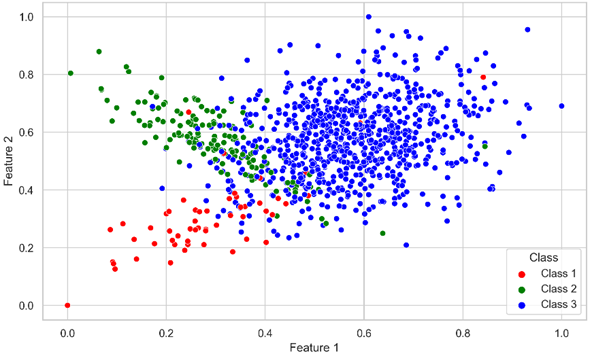
类别不平衡问题是机器学习领域的重要问题，表现为其中一类的实例数量明显少于其他类，以及存在类重叠的情况，导致标准机器学习模型在少数类上无法充分学习，造成预测性能显著下降。多分类不平衡问题比二分类更为复杂，但是目前针对多分类不平衡问题的研究较少。多分类问题的困难因素有：类别数量的增加、不平衡比的增加、多个类别的特征重叠、不同类别之间的相对关系，这些因素导致针对二分类不平衡问题设计的方法难以直接被应用于多分类。同时，现有的研究工作大部分都是以数据集的不平衡比例作为衡量不平衡程度的依据展开的，它并不能反映其他的不平衡因素，例如类别重叠的程度和实例的困难程度。

深度森林是一种基于决策森林模型实现的深度学习模型，具有不依赖梯度计算、级联自适应增长、超参数较少、预测性能好等优点，已经被用于解决各种实际问题。也有一些研究工作使用深度森林来解决不平衡学习问题，但是暂未有工作针对多分类不平衡学习设计新型的深度森林模型，同时目前也鲜有研究工作对enhanced vectors以外的信息增强的方式进行探索。

文章贡献

综合考虑现有多分类不平衡学习方法的局限性和相关研究工作的不足，本文提出了一种基于多类降解和特征构造的新型多分类不平衡学习深度森林算法，简称为MDGP-Forest。MDGP-Forest首先将数据拆解为多个二分类数据副本，以规避多个类别之间的复杂相互关系。接着通过增强向量得到每个实例的硬度，并以此为依据对副本进行欠采样。该步骤的目的是防止噪声实例引入负面的信息，同时提高对靠近决策边界的实例的关注。然后MDGP-Forest通过多个种群GP进行类别相关的特征构造，每个GP种群构造出的特征将帮助一个类别的实例更容易和其他类别区分开来。GP进行适应度评估时考虑了增强向量的相对重要性，鼓励构造能补充增强向量的信息的特征，而不是像原始深度森林那样重用原始特征。然后MDGP-Forest使用构造特征训练一个新的级联层。重复上述过程训练多层级联森林，直到满足停止条件。实验在35个数据集上对MDGP-Forest的性能进行充分的评估，实验结果表明MDGP-Forest在多分类不平衡问题上显著优于现有的方法，具有较高的预测性能。

本文方法

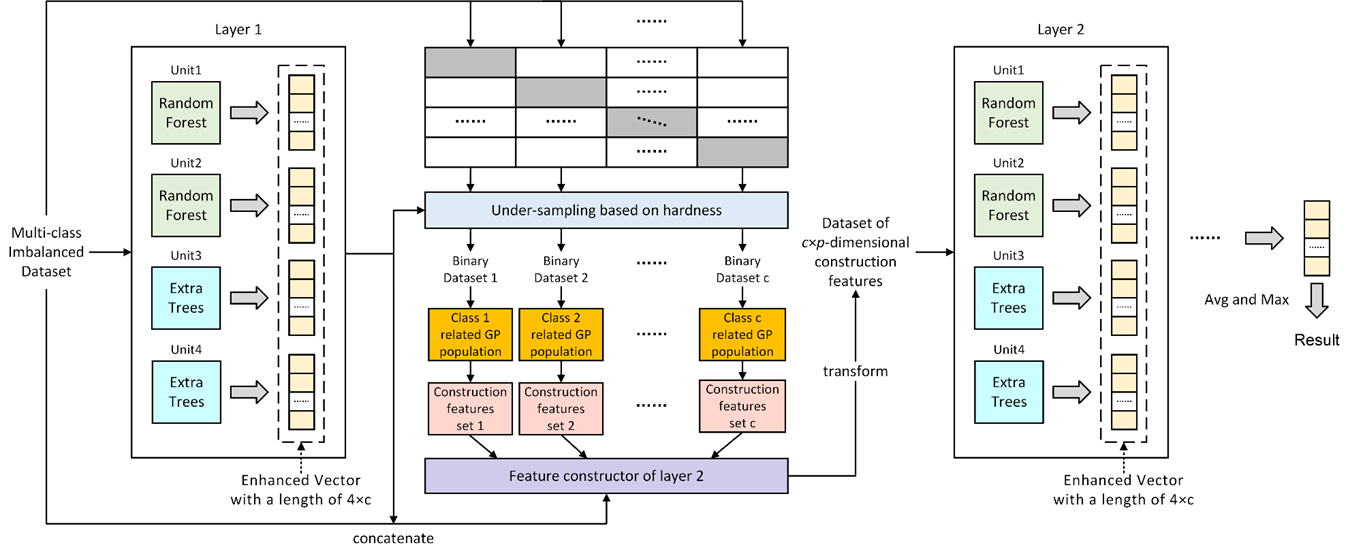
MDGP-Forest框架

给定一个包含 n 个实例和 c 个类别的数据集 D=(X, Y)，每个实例由一个 d 维特征向量 x_i 和一个对应的类别标签 y_i 组成。设 DF 为包含 T 层级联和每层对应的特征构造器 FC 的 MDGP-Forest 模型，其中每层级联 L_t 由 K 个决策森林模块 F 组成。由于设计新的决策森林模块来替换深度森林的原始设置并非本文的关注点，因此 MDGP-Forest 和 gcForest 使用的决策森林模块一样。
仅使用构造特征可能存在部分特征被忽略或重用的问题，导致信息丢失和过拟合，因此 MDGP-Forest 使用完整的原始特征训练第一层级联森林 L₁。对于一个包含 M 个决策树的森林模块，一个实例的预测向量 V 被定义为每棵决策树生成的类向量的平均值，如下公式所示。其中 q(x) 为 x 在第 i 棵决策树上所属的叶结点索引，w_i,j 为第 i 棵决策树的叶结点 j 上不同类别的实例的比例。

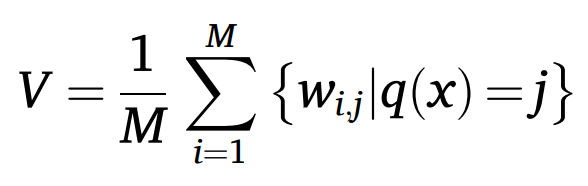
第 t 层级联的增强向量 E_t 通过对第 t 层的 K 个森林模块的预测向量拼接得到，如下公式所示。

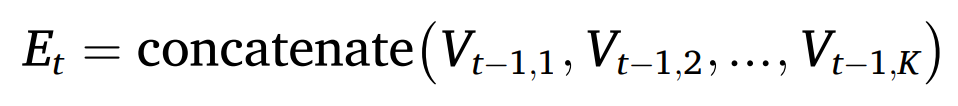
在训练第 t 层级联之前要通过多类降解与采样、类相关特征构造两个步骤对训练数据进行处理。在多类降解与采样阶段将把训练数据拆解为多个二分类数据副本，并从增强向量中得到每个实例的硬度，然后使用基于实例硬度的欠采样对数据副本进行处理。
接着将使用得到的数据副本作为多个 GP 种群的输入进行特征构造，种群中的每个 GP 个体对应一个构造特征的表达式。单个 GP 种群通过多轮进化和迭代之后获得特征构造器 FCS，将多个种群的 FCS 合并作为第 t 层级联的特征构造函数 FC_t。然后使用特征构造函数对原始特征进行转换，并和增强向量拼接得到第 t 层级联的输入特征 x_t，如下公式所示。

MDGP-Forest 在后续级联使用特征构造有两个方面的考虑：

1. 当不同的类别之间存在类重叠的情况时，使用原始特征难以准确地对重叠区域的实例进行分类；
2. 增强向量在后续的级联层次中将起到主导作用，此时原始特征的作用将很有限。

MDGP-Forest 使用转换为构造特征的完整数据集 X_t 训练第 t 层级联 L_t，然后对整个级联的性能进行评估。如果没有性能增益则训练过程终止，否则就重复上述步骤继续训练新一层的级联。由于改进停止条件并非本文的重点，MDGP-Forest使用 F1_macro 作为评估度量。综上所述，可以得到如算法 1 所示的 MDGP-Forest 的训练流程。

对新输入的实例进行分类时，实例将依次通过每个级联层次进行预测。在层次之间需要使用特征构造器生成新特征，并拼接增强向量。直到最后一层级联完成预测，将每个森林模块输出的预测向量进行融合得到最终的预测结果，如下公式所示。

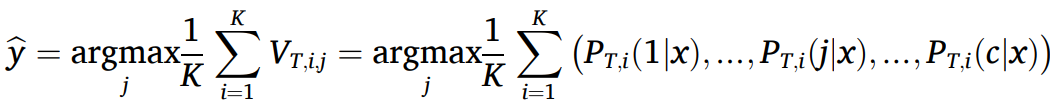
多类降解与重采样

MDGP-Forest 的多类降解与重采样模块的结构如下图所示，第一步是通过多类被降解将多分类数据转换为多个二分类数据副本，第二步是基于实例硬度对二分类数据副本进行欠采样处理。

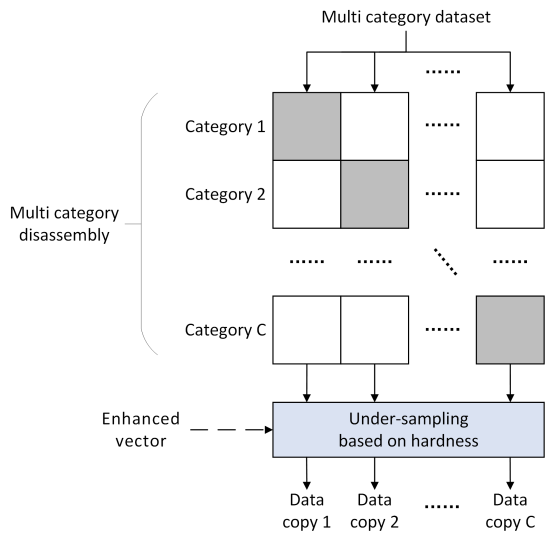
多类降解基于 OVA 策略实现，每次将一个类别作为正类，其他所有类别作为负类得到 c 个二分类数据集。选择 OVA 有 3 个原因：

1. OVA 可以获得固定数量的二分类数据集，不会显著增大特征构造阶段的计算开销；
2. 如果二分类数据集的正类包含多个类别时仍然存在类别重叠，使用 OVA 时正类至多包含一个类别；
3. 有研究证明搜索最优类别降解策略是 NP-hard 问题，设计其他策略可能导致模型过拟合。

但是 OVA 存在显著增大二分类数据集的不平衡比的问题，因此本文设计了一种基于实例硬度的采样策略做进一步的处理。实例的硬度定义为 1-p(y_i | x_i, h)，即越难被正确预测的实例硬度更大。对于决策森林而言可以将预测向量视为实例 x 被预测为不同类别的概率，因此 MDGP-Forest 中实例 (x_i, y_i) 在第 t 层级联的硬度将根据增强向量计算得到，如下公式所示。其中 P_t-1,j(y_i|x_i) 为 E_t 中第 j 个森林模块在实例 x_i 上对于类别 y_i 分配的概率。

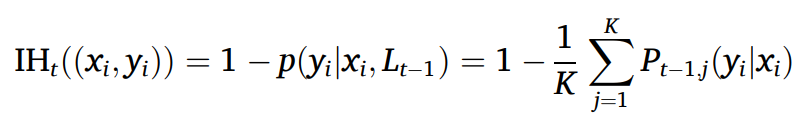
该硬度定义具有模型相关和在 MDGP-Forest 训练时动态变化的特点。接着设置实例硬度阈值 θ，结合实例的预测标签 y^和真实标签 y 可以将实例分为不同的类型，包括：预测正确容易实例（Easily Predicted Correct Instances, EPCIs）、预测错误容易实例（Easily Predicted Incorrect Instances, EPIIs）、预测正确非容易实例（Non-easily Predicted Correct Instances, NPCIs）、预测错误非容易实例（Non-easily Predicted Incorrect Instances, NPIIs），如下表所示。

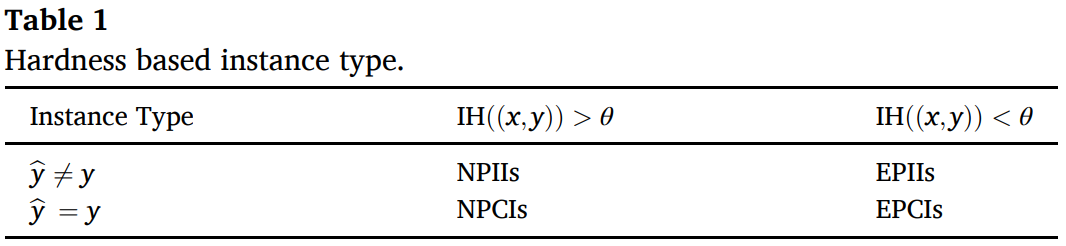
接着基于实例类型对数据副本进行欠采样操作：

1. 当二分类副本中的正类是少数类时，将移除该副本中负类的 EPCIs 和 EPIIs。这是因为模型对于 EPCIs 得到正确的预测结果相对容易，移除这些实例可以让特征构造阶段得到易于区分一个类别和其他类别的特征。而一个负类实例被识别为 EPIIs 时，说明这些实例极其容易被错分为正类样本，很有可能是噪声；
2. 当二分类副本中的正类是多数类时，将移除该副本中正类的EPCIs，根据 OVA 的原理可知该类别的实例数量显著多于其他类别，因此需要通过移除这些实例让特征构造阶段更关注靠近决策边界的实例。

该模块的工作流程如算法 2 所示。需要注意的是，此处的欠采样操作仅对二分类数据副本进行处理，目的是为了引导特征构造阶段构造出更具有可分性的特征。在级联的森林模块的训练阶段仍然使用完整的训练集，从而避免了信息丢失的问题。

类相关的 GP 特征构造

完成多类降解与重采样步骤后 MDGP-Forest 将进行类相关的 GP 特征构造，该步骤的目的是构造一组高质量的新特征，缓解特征重叠问题。
特征构造主要通过多个 GP 种群实现，如下图所示。每个二分类数据副本将对应一个 GP 种群，使一组构造特征与一个具体的类别相关。每个种群完成进化迭代后得到一个对应单个类别的特征构造器 FCS，当所有种群的进化停止时，将所有 FCS 合并以获得一个整体特征构造器FC_t,在开始下一层的训练之前转换特征。

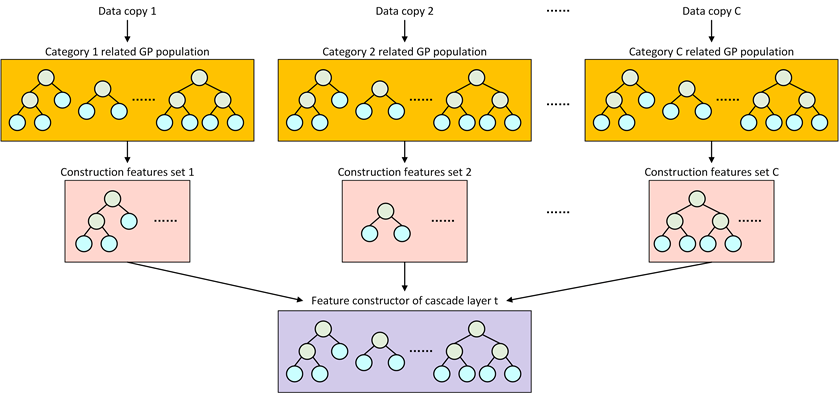
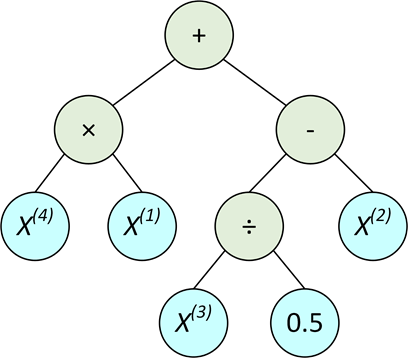
一个 GP 种群中包含 P 个个体，每个个体对应一个构造特征。GP 个体的结构为一棵表达式树，原始特征通过该表达式生成一个新特征。个体的叶子结点由 d 个特征对应的索引和常数构成，非叶子节点由运算符构成。

单个 GP 种群的工作流程为：

1. 对种群进行随机初始化，生成第一代种群；
2. 对个体进行解析得到一组构造特征，并计算每个特征对应的适应度值；
3. GP 种群将通过交叉、变异和选择操作生成新一代种群，并将适应度较高的精英个体保留到下一代；
4. 不断重复第二阶段、第三阶段的步骤，以迭代更新种群，直至达到最大迭代数才停止；
5. 选择最终代中适应度值排名较高的 p 个个体构成对应单个类别的特征构造器。

运行适应度评估函数后将得到每个个体的适应度值，用于在进化过程中指导 GP 得到更好的个体，决定了得到的特征质量。为了防止构造特征的信息被增强向量淹没，本研究设计了一种模型相关的构造特征的增量重要性评估函数。首先使用当前代的所有个体对应的构造特征作为临时构造器 FC_temp 对原始特征进行转换，然后将其和增强向量 E_t 拼接得到输入特征 X^。使用 X^ 训练一棵 CART ，然后使用 Mean Decrease Impurity(MDI) 方法实现特征重要性归因。该方法主要有以下几个优势：

1. 这是一种模型相关的特征重要性评估方案，实现对增强向量具有信息互补作用的构造特征的生成；
2. MDGP-Forest 的级联层由决策森林模块构成，使用 CART 进行特征重要性归因与这种设置相符合；
3. 该方法具有可接受的计算开销，在每一轮迭代只需要训练一个决策树即可实现适应度评估。

在遗传算子方面，本文使用锦标赛选择算子，交叉算子选择单点交叉，突变算子选择单点变异。GP 使用精英保留策略来保留种群中适应度高的个体，它们将在每一次进化中被更新。当 GP 运行到最大代数后，得到与单个类别对应的特征构造器 FCS。综上所述，该步骤的整体流程如算法 3 所示。

实验结果

数据集和实验设置

本文从 UCI 和 OpenML 收集了 20 个多分类不平衡数据集和 15 个多分类数据集，这些数据集的基本信息分别如下表所示。多分类不平衡数据集的不平衡比至少为 2，虽然使用的多分类数据集的实例数量的失衡程度有限，但它们也可能存在类重叠。读取数据时使用 Min-Max 标准化法进行处理，使用的主要评估指标包括 F1、G-means、MCC，以宏平均的方式计算。

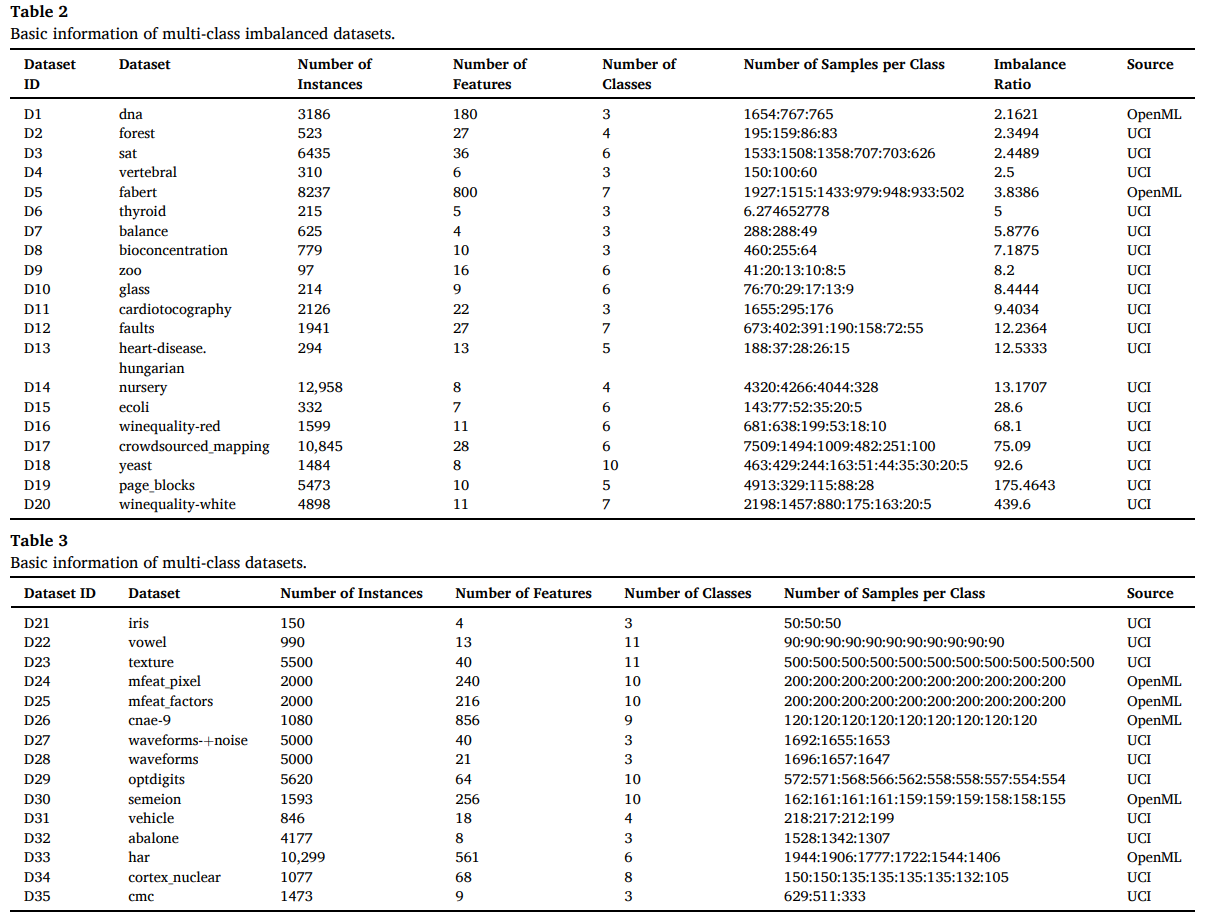
MDGP-Forest 的参数主要包括级联森林的参数和 GP 种群的参数，默认的设置如下表所示。特征生成运算符方面，GP 设置了加、减、乘、除、开方、取反这几个运算符。

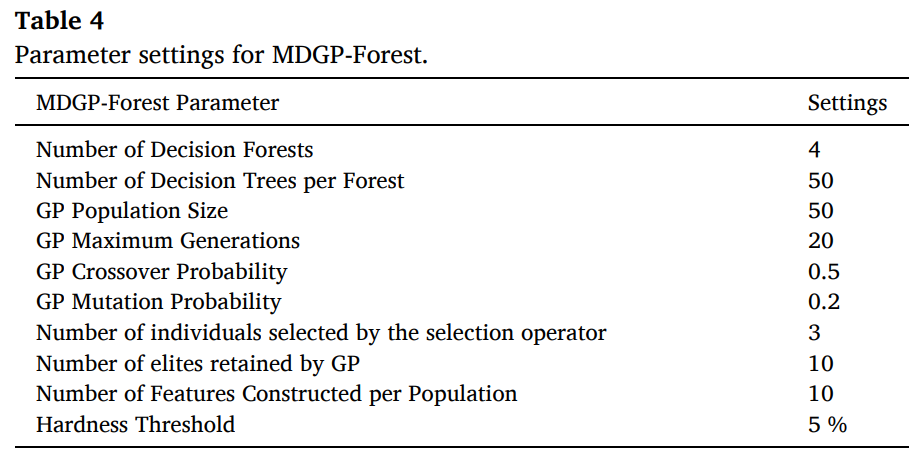
对比实验

通过对比实验验证 MDGP-Forest相比其他 baselines 或 State-of-the-Art 在多分类不平衡问题上具有更优越的预测性能，用于对比的算法如下。每个算法都运行 10 次五折交叉验证，通过取平均值得到每个评估指标的实验结果。

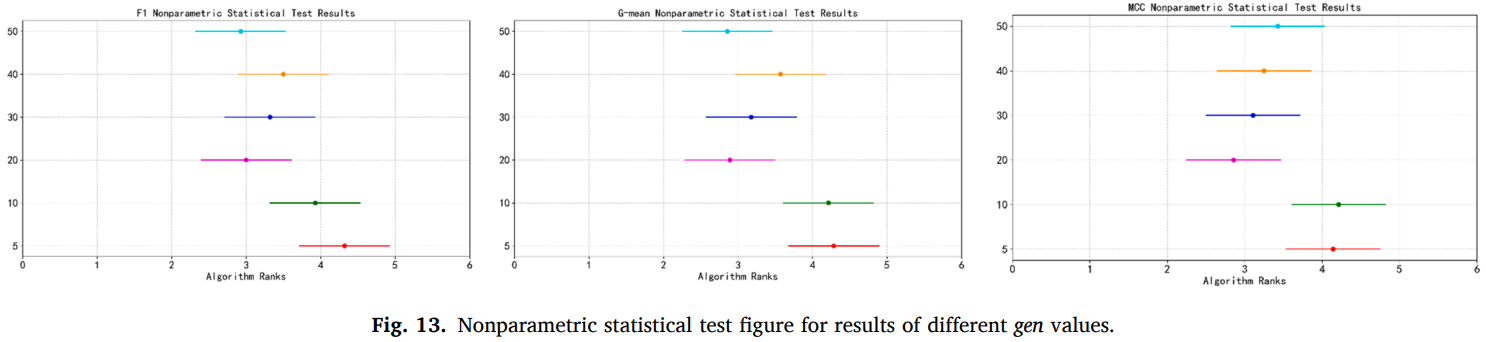
使用 Friedman 检验和 Nemenyi 后续检验进行分析和结果可视化，从实验结果可以明显地看出，本研究提出的 MDGP-Forest 在 F1、G-mean 和 MCC 上都获得了相比其他算法更好的分类性能。

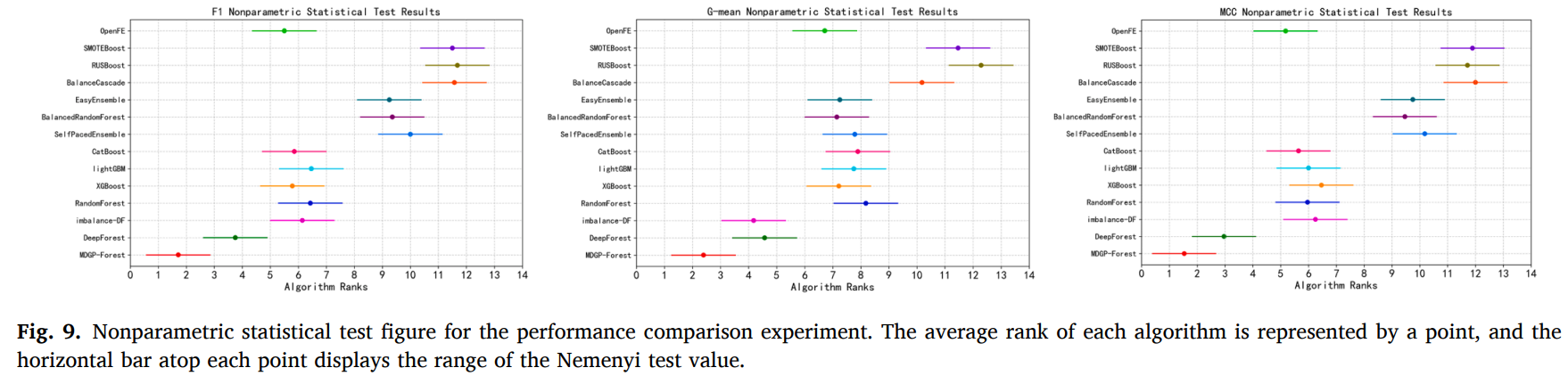
消融实验

消融实验将通过删除 MDGP-Forest 的模块或者更改设置并观察算法的性能变化，从而验证它们的有效性。每个算法变体都在所有数据集上运行1 0 次五折交叉验证，然后通过 Friedman 检验和 Nemenyi 检验进行展示。设置了 4 种 MDGP-Forest 变体进行比较：

变体	说明
No_HR	No Hardness Resampling，不进行基于硬度的欠采样步骤，直接进行类相关的特征构造
D-RUS	Disassembly with RUS，使用随机欠采样处理二分类数据集，不使用基于硬度的欠采样方法
No_MD	No Multiclass Disassembly，不进行多分类降解，而是直接运行基于硬度的欠采样和类相关的特征构造
No_OF	No Original Features，在训练第一层级联时就使用构造特征，其他设置和 MDGP-Forest相同

各个变体的 F1、G-mean、MCC 的假设检验结果如图所示，可见各个指标呈现的趋势是一致的。预测性能最差的是 D-RUS 和 No_MD，排名第二和第三的变体分别是 No_OF 和 No_HR，MDGP-Forest 在各个指标上获得的预测性能最好。消融实验验证了 MDGP-Forest 中各个模块或设置的有效性，每个模块都给 MDGP-Forest 在多分类不平衡问题上的优越性能提供了积极作用。

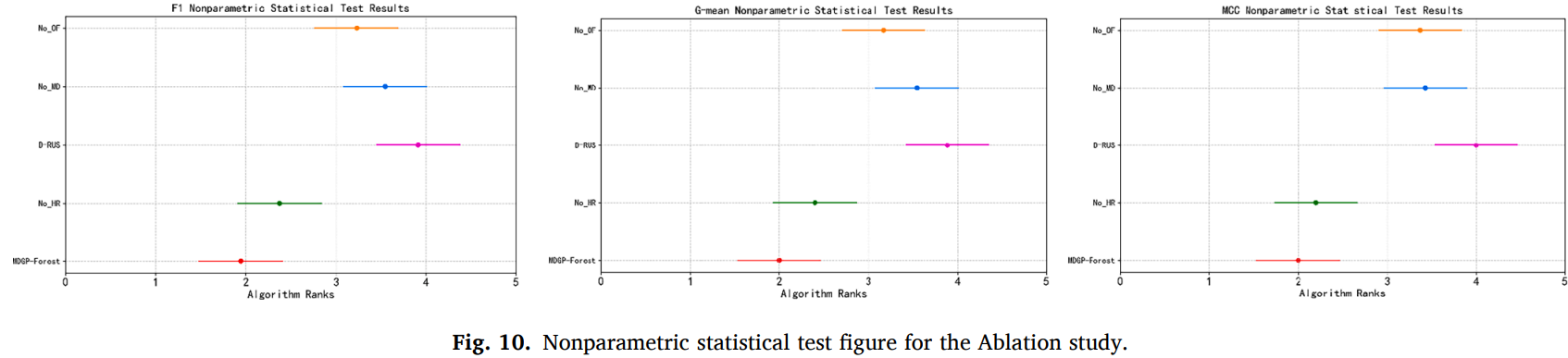
调参实验

正文中的调参实验涉及 3 个主要的参数：硬度阈值、每一代构造的特征数量、GP 最大代数。在支撑材料中，还包括 6 个额外的超参数实验分析：crossover rate、mutation rate、population size、max depth、min samples split、min samples leaf。
硬度阈值用于区分实例的难易程度，硬度低于该值的实例被认为是容易实例。MDGP-Forest 设置 4 个不同的值，然后在所有数据集上运行 10 次五折交叉验证和Friedman检验。检验的结果如图所示，可见相对更保守的 5% 是一个较为合适的设置。

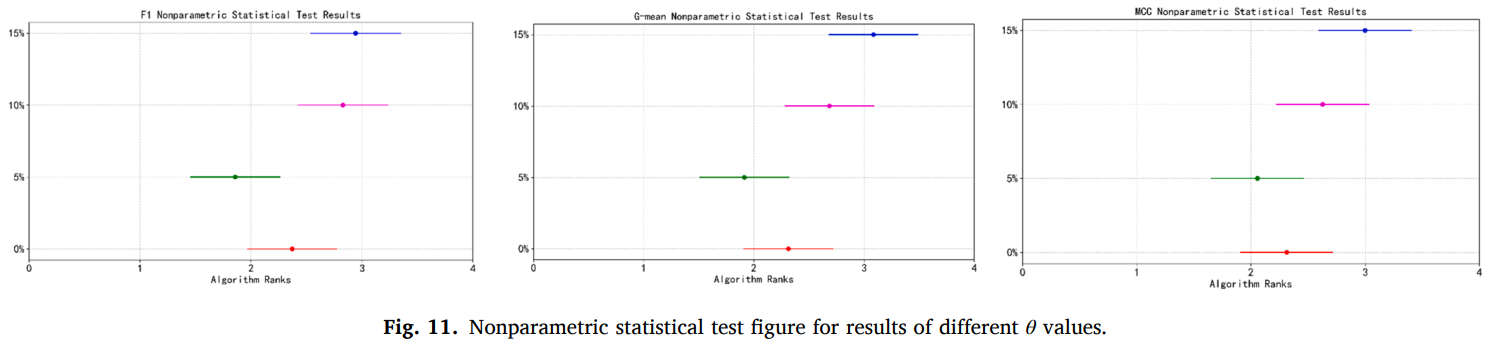
每一代构造的特征数量设置的值越高则新特征数量越多，MDGP-Forest 设置 4 个不同的值，在除高维数据集以外的数据集上运行 10 次 5 折交叉验证和 Friedman 检验。结果如图所示，参数设置为 10、20、50 时优于设置为 5 的情况，综合来看设置为 10 最优。当构造的新特征数量较少时，可能引入的信息不足导致对 MDGP-Forest 的性能提升不明显。当构造的新特征数量较多时，可能会造成一定的冗余。当设置为 50 时，会将适应度较低的个体也作为构造特征。它们可能对模型带来一定的干扰，同时还会增加训练模型的计算开销。

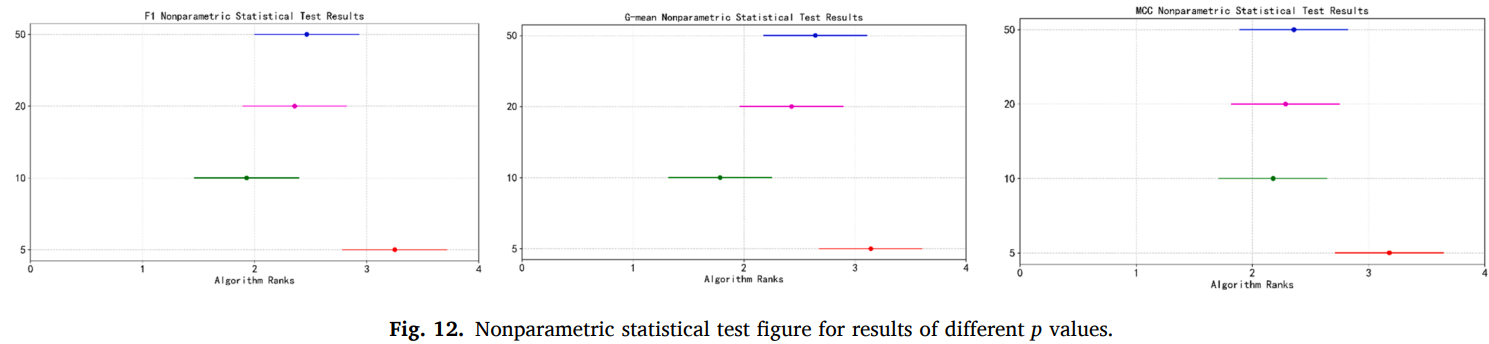
GP 最大代数设置的值越高，GP 的迭代次数将越多，MDGP-Forest 设置 6 个不同的值。结果如图所示，可见设置为 20、30、40、50 时在各个评估指标上优于设置为 5、10 的情况，这是因为当值较小时可能存在运行结果差异较大和搜索不充分的问题。设置为 30、40 时性能比设置为 20 时差，虽然较大的g有助于GP搜索更多的可行解，但也可能陷入局部最优解，导致过拟合。设置为 50 时在 F1 和 G-mean 上获得了更高的指标，这可能是在较多次的迭代中避免了局部最优解，但是此时优势并不明显。所以该超参数也需要设置为一个适中的值，10~30 之间可能是较为理想的范围。

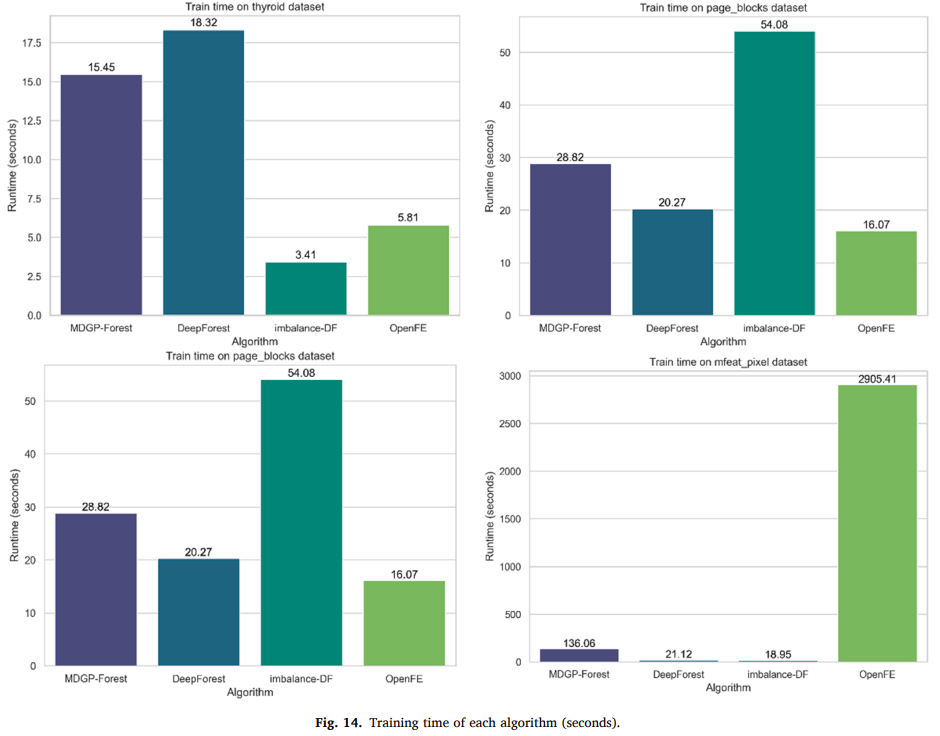
运行时间

MDGP-Forest 和 DeepForest、imbalance-DF、OpenFE 的训练时间进行比较，实验统计每个算法在上述数据集中的一次五折交叉验证的平均运行时间，单位是秒。这些算法在所有数据集上的运行时间在补充材料中，正文展示了 thyroid、page_blocks、optdigits、mfeat_pixel 四个典型的结果，如图所示。可见在大部分情况下，MDGP-Forest 的运行时间长于 Deep Forest，但在可接受的范围内。MDGP-Forest 在小规模数据集上的运行时间和 Deep Forest 接近。相比于 Expand-and-Reduce 类型的 OpenFE 算法，MDGP-Forest 在特征数量较多的数据集上的运行时间具有显著优势。

创新点

本文的主要贡献如下：

1. 提出了一种新型多分类不平衡学习深度森林算法,该算法能有效针对类重叠问题，获得了优越的多分类不平衡预测性能；
2. 设计了一种多类降解与采样策略，有效应对了多类别不平衡数据集的复杂相互关系；
3. 设计了一种用于级联森林层次的类相关特征构造的多种群 GP，它在考虑相对增强向量的增量特征重要性；
4. 通过大量的数据集和广泛的实验，充分验证了 MDGP-Forest 的有效性和高预测性能。