感知机与神经网络

什么是感知机

  • 感知机（Perrceptron)又称神经元（Neuron）是神经网络（深度学习）的起源算法，1958年由康奈尔大学心理学教授弗兰克.罗森布拉特提出，它可以接受多个输入信号，产生一个输出信号。
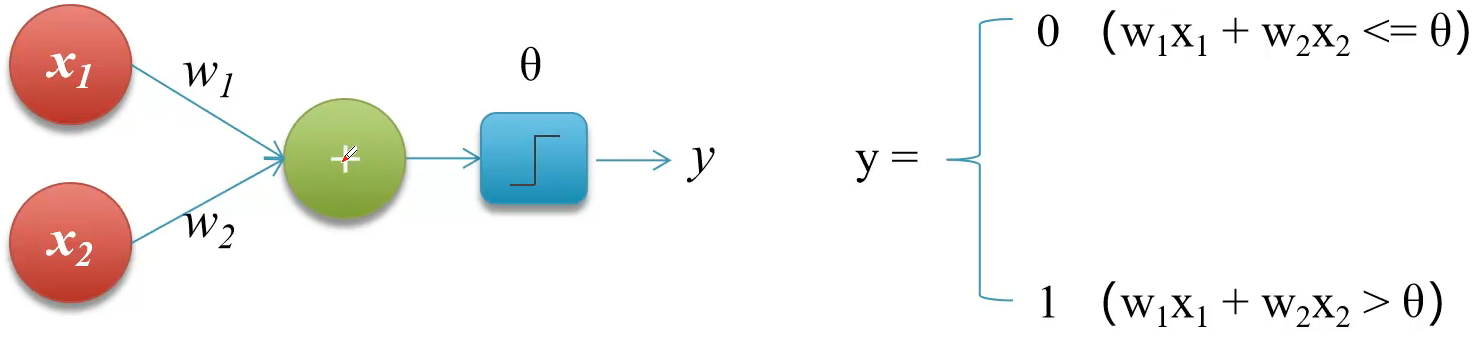
    image

其中，X1和X2称为输入，w1和w2为权重，+表示运算的规则，Θ为阈值，y为输出
运算规则只有w1x1+w2x2，若结果小于等于Θ得到输出为0，大于Θ则输出1。

感知机的功能

  • 实现逻辑运算，包括逻辑和（And）、逻辑或（Or）**感知机无法处理”异或“问题，多层感知机可以处理异或问题
  • 实现自我学习
    学习：反复执行某一个过程，提升机器的能力
    在感知机表达式中x1x2和y值是已知的，w1，w2和0是未知的，当具有一定量样本时，将样本喂给感知机得到一个y值，反复循环迭代，迭代式不断调整w1，w2和0，就可以使得输入x1，x2输出结果为y，此过程称为感知机的学习
  • 组成神经网络

代码实现逻辑运算

逻辑和

#自定义感知机
#实现逻辑和
def AND(x1,x2):
    w1,w2 = 0.5,0.5 #两个权重
    theta = 0.7 #阈值
    tmp = x1*w1+x2*w2
    if tmp <=theta:    return 0
    else:return 1
if __name__ == '__main__':
    print(AND(1,1))

逻辑或

def OR(x1,x2):
    w1,w2 = 0.5,0.5 #两个权重
    theta = 0.2 #阈值
    tmp = x1*w1+x2*w2
    if tmp <=theta:    return 0
    else:return 1
if __name__ == '__main__':
    print(OR(1,1))#1
    print(OR(1,0))#1
    print(OR(0,0))#0

异或

#自定义感知机
#实现逻辑和
def AND(x1,x2):
    w1,w2 = 0.5,0.5 #两个权重
    theta = 0.7 #阈值
    tmp = x1*w1+x2*w2
    if tmp <=theta:    return 0
    else:return 1
# 实现逻辑或
def OR(x1,x2):
    w1,w2 = 0.5,0.5 #两个权重
    theta = 0.2 #阈值
    tmp = x1*w1+x2*w2
    if tmp <=theta:    return 0
    else:return 1
#实现异或
def XOR(x1,x2):
    s1 = not AND(x1,x2) #对x1，x2做逻辑和计算再去非
    s2 =OR(x1,x2) #直接对x1.x2做逻辑和运算
    y = AND(s1,s2)
    return y
if __name__ == '__main__':
   print(XOR(1,1)) #0
   print(XOR(1,0)) #1
   print(XOR(0,1)) #1
   print(XOR(0,0)) #0

神经网络

感知机由于结构简单，完成的功能十分有限。可将若干个感知机连在一起，形成一个级联网络结构，这个结构称为”多层前馈神经网络“。所谓”前馈“是指将前一层的输出作为后一层的输入的逻辑结构。每一层神经元仅与下一层的神经元全连接。但在同一层之内的神经元彼此不连接，而且跨层之间的神经元，彼此也不相连。

神经网络的功能

通用近似定理

对于任意复杂度的连续波莱尔可测函数f，仅仅需要一个隐含层，只要这个隐含层包含足够多的神经元，前馈神经网络使用挤压函数作为激活函数，就可以任意精度来近似模拟f若想增加f的近似精度，单纯依靠增加神经元的数目即可实现。
该定理表明，前馈神经网在理论上可近似解决任何问题

神经网络的优点

增加网络的层数会显著提升神经网络系统的学习性能。

激活函数

  • 在神经网络中，将输入信号的总和转换为输出信号的函数被称为激活函数（activation function)
    image

为什么使用激活函数

  • 激活函数将多层感知机输出转换为非线性，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。
  • 若一个多层网络，使用连续函数作为激活函数的多层网络，称之为“神经网络”，否则称为“多层感知机”。激活函数是区分多层感知机和神经网络的依据

常用激活函数

阶跃函数

阶跃函数是一种特殊的连续时间函数，是一个从0跳变到1的过程，函数形式与图像如下：
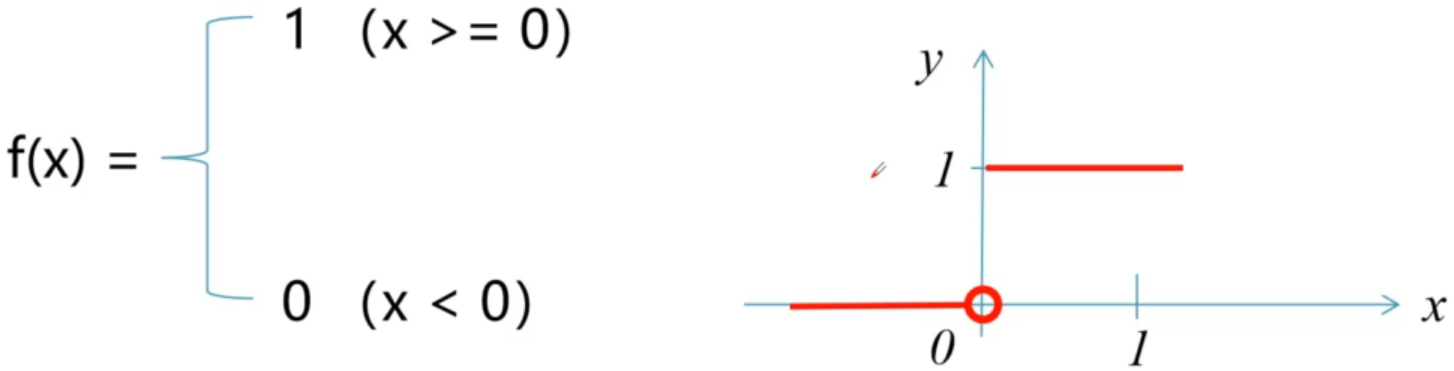
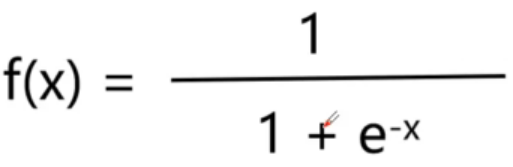
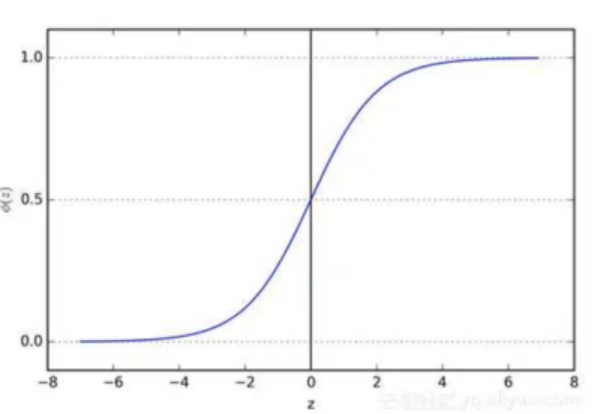
image

sigmoid函数

sigmoid函数也叫Logistic函数，用于隐层神经元输出，取值范围为（0，1）它可以将一个实数映射到（0,1）的区间，可以用来做二分类
image
image

  • 优点：平滑、易于引导
  • 缺点：激活函数计算量大，反向传播求误差梯度是，求导涉及除法；反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练，（应避免发生梯度消失的情况）

tanh（双曲正切）

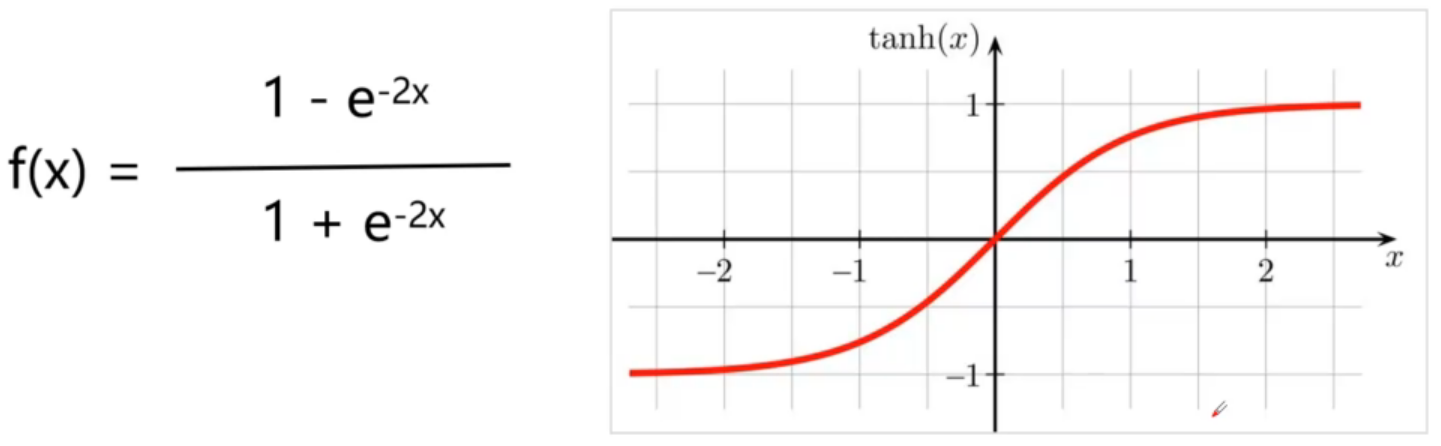
image

  • 优点：平滑、易于求导；输出均值为0，收敛速度要比sigmoid快，从而可以减少迭代次数
  • 缺点：梯度消失

Relu(修正线性单元)

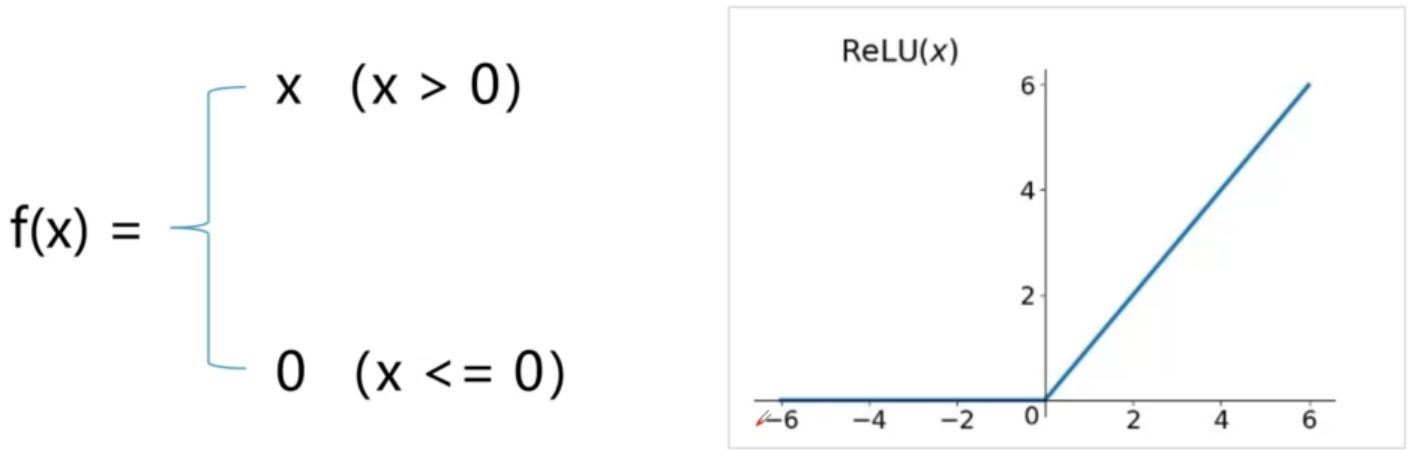
image

  • 优点：
    1.更加有效率的梯度下降以及反向传播，避免了梯度爆炸和梯度小时问题
    2.计算过程简单

Softmax

Softmax函数定义如下
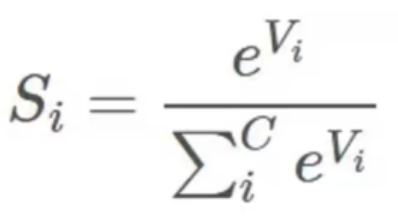
image
其中Vi是分类器前级输出单元的输出。i表示类别索引，总的类别个数为C。Si表示的是当前元素的指数与所有元素指数和的比值。通过Softmax函数可将多类的输出数值转换为相对概率，而这些值得累和为1.
Softmax函数常用在最后一层输出层

小结

  • 多层前馈网络：若干个感知机组合成若干层网络，上一层输出作为下一层输入
  • 激活函数：将计算结果转换为输出的值，包括阶跃函数，sigmod、tanh、Relu
posted @ 2022-02-13 19:58  9974  阅读(543)  评论(0)  编辑  收藏  举报
快递查询