离散傅里叶变换(DFT)的Python实现

离散傅里叶变换（Discrete Fourier Transform，DFT）

Fourier分析是指通过傅里叶级数，表示和分析周期信号。Fourier变换则是将这些方法扩展至非周期信号中。

Fourier变换可以将信号分解至一系列频率不同的sin或者cos信号的和，Fourier系数是这些sin信号对应的幅值。通常我们分析这些Fourier系数的平方，绘制功率频谱，用以分析信号的频率特征。

离散傅里叶变换则是Fourier变换的离散版本。

本文主要讨论DFT的实现方法，主要包括DFT算法原始实现、频谱截断与幅值标准化，不过多涉及Fourier变换的理论。欢迎讨论或指正错误。

对于周期信号，我们可以直接应用DFT，公式定义如下：

\(X_k = \sum_{n=0}^{N-1}{x_n\cdot e^{-i2\pi{kn/N}}} = \sum_{n=0}^{N-1}{x_n[cos(2\pi{kn/N}) -i\cdot sin(2\pi{kn/N})]}\)

其中，

• \(N\): 当前信号的总长度，
• \(x\)为原始周期信号，
• \(X\)为Fourier系数，
• \(k\)为当前频率点，\(k\in [0,N-1]\)。

原始DFT算法实现

我们可以利用原始DFT公式，使用python，写出一个Fourier系数计算函数（参考Python Numerical Methods)。

点击查看代码

def dft_raw_version(x: np.array, fs: int) -> np.array, np.array:
    """
        原始DFT实现.
    :param x: 原始信号.
    :param fs: 信号采样频率.
    :return: Fourier系数.
    """

    # Fourier系数计算
    N = len(x)
    n = np.arange(N)
    k = np.reshape(n, (N, 1))
    we = np.exp(-2j * np.pi * k * n / N)
    # X为最终的Fourier系数
    X = np.dot(we, x)

    # 生成频率轴
    ts = N / fs
    freq = n / ts

    return freq, X

随后我们生成一个多个频率混合的sin函数，\(f(x) = 3 * sin(2\pi t) + 1 * sin(2\pi 4t) + 2 * sin(2\pi 8t) + 0.5 * sin(2\pi 16t)\)，基于python的生成函数如下：

点击查看代码

    # 信号原始采样频率以及信号长度
    fs, length = 100, 4
    ts = np.arange(0, length, 1 / fs)
    # 设置4个频率分量
    frequency_factor = [1, 4, 8, 16]
    amplitude_factor = [3, 1, 2, 0.5]
    # 生成周期信号
    periodic_signal_x = None
    for f, a in zip(frequency_factor, amplitude_factor):
        periodic_component = a * np.sin(2 * np.pi * f * ts)
        if periodic_signal_x is None:
            periodic_signal_x = periodic_component
        else:
            periodic_signal_x += periodic_component

生成的sin函数如下图所示。

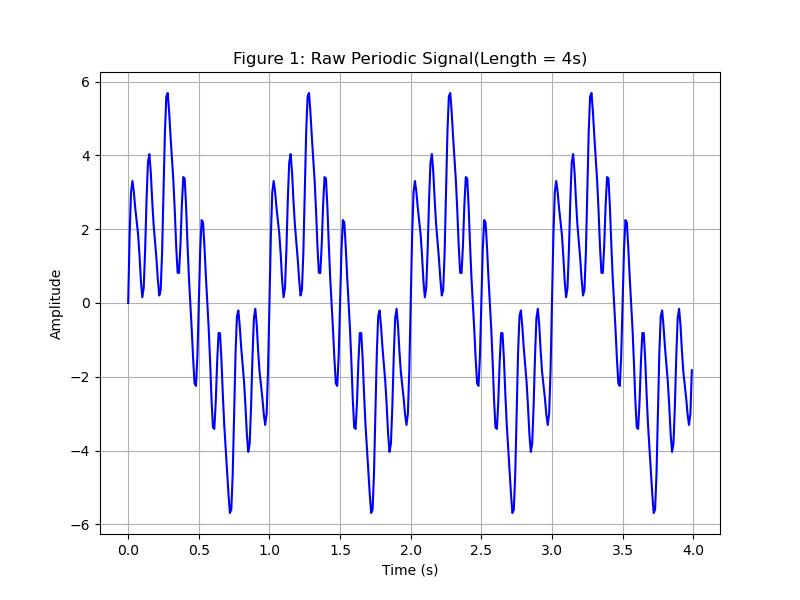
我们期待利用DFT函数，得到对应的Fourier系数，并能与我们设置的频率分量能够对应。下图是我们根据dft_raw_version函数得到的频谱图，横轴为频率，纵轴为傅里叶系数的绝对值，具体的python代码如下：

点击查看代码

    frequencies, fourier_coefficients = dft_raw_version(periodic_signal_x, fs)
    amplitudes = np.abs(fourier_coefficients)

对应的频谱图如下所示。

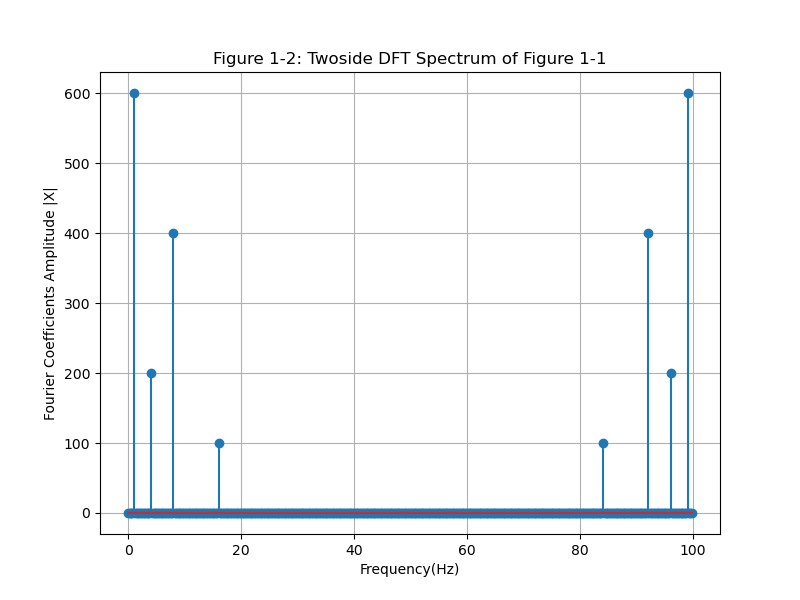
从Figure1-2中，我们可以该频谱图的特点：

• 以横轴中心点（在图中是50Hz）轴对称；
• 观察0-50Hz，频谱中对应的频率分量点能够对应，但频率分量点对应的幅值要明显高于预设的幅值。（在示例中，我们设置的频率分量点分别为（1，4，8，16）Hz，与图中Fourier系数绝对值较高的频率点对应。但幅值不对应，我们设置的幅值为（3，1，2，0.5），频谱中为（600，200，400，100）。）

50-100Hz通常称为负频率，即-50-0Hz，其中\(X_{-k} = \overline{X_k})\)，在绘制频谱时我们只关心正频率即可。
幅值与我们预设幅值不对应，主要是我们未对Fourier系数做标准化。

所以我们需要再做两件事儿，就可以得到我们想要的频谱图：

• 截断0-50Hz的频谱；
• 对Fourier系数进行标准化。由于正、负频率的Fourier共同构成频谱的总能量，但我们只画了正频率部分，要想得到与我们预设的幅值一样的频谱，我们需要除以\(\frac{N}{2}\)而不是\(N\)。

经过标准化的DFT函数如下：

点击查看代码

def dft_normalized_version(x: np.array, fs: int) -> np.array, np.array:
    """
    得到标准化后的Fourier系数和频率轴. 对比dft_raw_version, 增加了两个操作.
    1. 只保留0-50Hz的频谱;
    2. 对频谱进行标准化, 除以N/2.

    :param x: 原始信号.
    :param fs: 信号采样频率.
    :return: Fourier系数.
    """

    # Fourier系数计算
    N = len(x)
    n = np.arange(N)
    k = np.reshape(n, (N, 1))
    we = np.exp(-2j * np.pi * k * n / N)
    # X为最终的Fourier系数
    X = np.dot(we, x)

    # 生成频率轴
    oneside_N = N // 2
    ts = N / fs
    freq_half = n[:oneside_N] / ts
    # Fourier系数截断与标准化后
    oneside_X_norm = X[:oneside_N] / oneside_N

    return freq_half, oneside_X_norm

使用标准化DFT函数得到的频谱图如下所示。

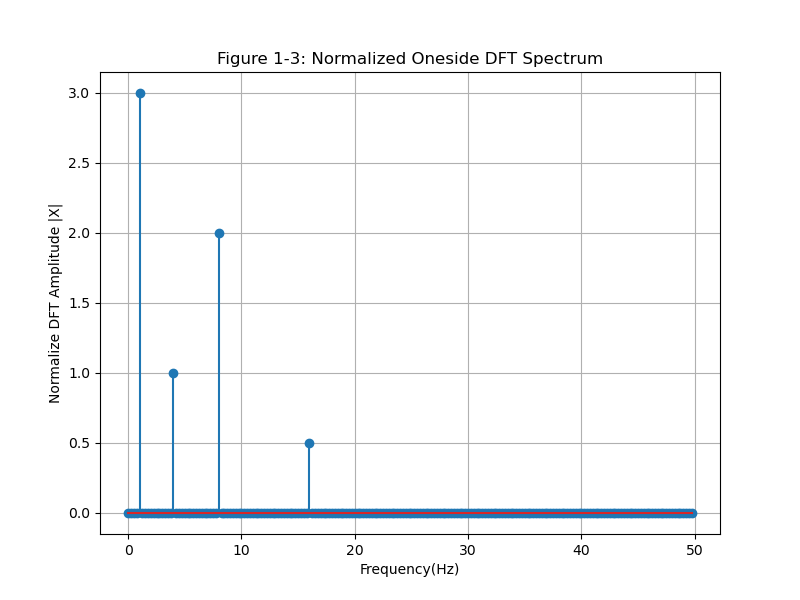
在实际应用中，使用单边、经过标准化的频谱更多一些。

数据长度N对频谱的影响

在我们的DFT算法中，有两个参数，数据的采样频率fs和数据长度N。
从实现代码中可以看出，数据长度N越大，频谱的间隔越小，频谱也就更加地平滑。

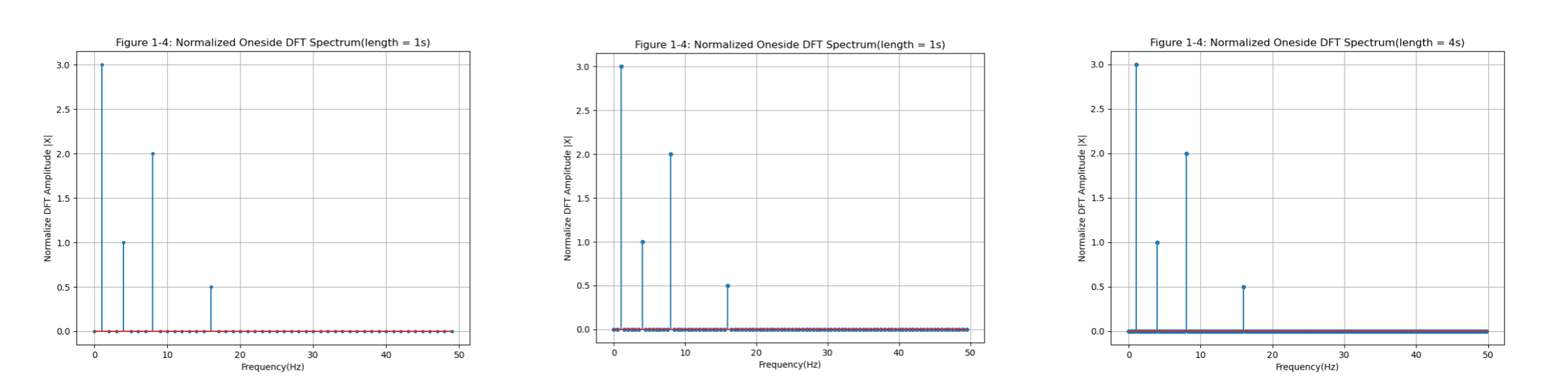
在周期信号的分析中，单个周期的信号就可以获得频谱中所有的信息，所以没必要延长数据的长度。在本例中，sin分量最大周期为1，所以理论上我们使用1s的数据即可。

关于fs的内容后续补充。

完整代码

点击查看代码

"""
    DFT简要实现与验证demo.
    Author: limekebab.
    E-mail: zzklove3344@hotmail.com.
"""

import numpy as np
import matplotlib.pyplot as plt


def dft_raw_version(x: np.array, fs: int) -> np.array:
    """
        原始DFT实现.

    :param x: 原始信号.
    :param fs: 信号采样频率.
    :return: Fourier系数.
    """

    # Fourier系数计算
    N = len(x)
    n = np.arange(N)
    k = np.reshape(n, (N, 1))
    we = np.exp(-2j * np.pi * k * n / N)
    # X为最终的Fourier系数
    X = np.dot(we, x)

    # 生成频率轴
    ts = N / fs
    freq = n / ts

    return freq, X


def dft_normalized_version(x: np.array, fs: int) -> np.array:
    """
    得到标准化后的Fourier系数和频率轴. 对比dft_raw_version, 增加了两个操作.
    1. 只保留0-50Hz的频谱;
    2. 对频谱进行标准化, 除以N/2.

    :param x: 原始信号.
    :param fs: 信号采样频率.
    :return: Fourier系数.
    """

    # Fourier系数计算
    N = len(x)
    n = np.arange(N)
    k = np.reshape(n, (N, 1))
    we = np.exp(-2j * np.pi * k * n / N)
    # X为最终的Fourier系数
    X = np.dot(we, x)

    # 生成频率轴
    oneside_N = N // 2
    ts = N / fs
    freq_half = n[:oneside_N] / ts
    # Fourier系数截断与标准化后
    oneside_X_norm = X[:oneside_N] / oneside_N

    return freq_half, oneside_X_norm


def dft_demo() -> None:
    """
        DFT Demo.
    :return:
    """

    # 信号原始采样频率以及信号长度
    fs, length = 100, 4
    ts = np.arange(0, length, 1 / fs)
    # 设置4个频率分量
    frequency_factor = [1, 4, 8, 16]
    amplitude_factor = [3, 1, 2, 0.5]
    # 生成周期信号
    periodic_signal_x = None
    for f, a in zip(frequency_factor, amplitude_factor):
        periodic_component = a * np.sin(2 * np.pi * f * ts)
        if periodic_signal_x is None:
            periodic_signal_x = periodic_component
        else:
            periodic_signal_x += periodic_component

    # 计算Fourier系数
    frequencies, fourier_coefficients = dft_raw_version(periodic_signal_x, fs)
    amplitudes = np.abs(fourier_coefficients)

    # 原始信号绘图
    fig, ax = plt.subplots(1, 1, figsize=[8, 6])
    ax.plot(ts, periodic_signal_x, c='blue')
    ax.set_title("Figure 1-1: Raw Periodic Signal(Length = 4s)")
    ax.set_xlabel("Time (s)")
    ax.set_ylabel("Amplitude")
    ax.grid()
    plt.show(dpi=400)

    # 绘制频率-幅值图, 双边频谱
    fig, ax = plt.subplots(1, 1, figsize=[8, 6])
    # Fourier系数是复数, 可以取平方或者取模
    markerline, stemline, baseline = ax.stem(frequencies, amplitudes)
    ax.set_title("Figure 1-2: Twoside DFT Spectrum of Figure 1-1")
    ax.set_xlabel("Frequency(Hz)")
    ax.set_ylabel("Fourier Coefficients Amplitude |X|")
    plt.setp(markerline, markersize=4)
    ax.grid()
    plt.show(dpi=400)

    # Fourier系数按频率中轴线对称, 所以我们只画一半的频谱就可以
    # 可以对Fourier系数的幅值进行标准化, 得到与我们预设的幅值相等的序列
    frequencies_oneside, fourier_coefficients_oneside = dft_normalized_version(periodic_signal_x, fs)
    amplitudes_oneside = np.abs(fourier_coefficients_oneside)

    # 绘制频率-幅值图, 单边频谱,
    fig, ax = plt.subplots(1, 1, figsize=[8, 6])
    # Fourier系数是复数, 可以取平方或者取模
    markerline, stemline, baseline = ax.stem(frequencies_oneside, amplitudes_oneside)
    ax.set_title(f"Figure 1-4: Normalized Oneside DFT Spectrum(length = {length}s)")
    ax.set_xlabel("Frequency(Hz)")
    ax.set_ylabel("Normalize DFT Amplitude |X|")
    ax.grid()
    plt.setp(markerline, markersize=4)
    plt.show()


if __name__ == '__main__':
    dft_demo()