python函数---匿名函数、递归、二分查找

1     lamda匿名函数

目的：为了解决一些简单的需求而设计的一句话函数，所有的匿名函数的函数名都是lamda

语法：

函数名 = lambda 参数: 返回值

注意:

（1）函数的参数可以有多个. 多个参数之间用逗号隔开

（2）. 匿名函数不管多复杂. 只能写一⾏, 且逻辑结束后直接返回数据

（3）. 返回值和正常的函数一样, 可以是任意数据类型

 

 

案例：

a = lambda a,b: max(a,b)
print(a(2,5))
print(a.__name__)   #<lambda>

坑：

 

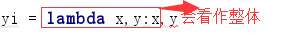
->正确的方式yi = lambda x,y:(x,y)

 补充：

匿名函数可以用在类里面：

案例：

class Foo:
    v= lambda self,x : x+1

obj = Foo()
print(obj.v(1))     #2

# ---->相当于
class Foo:
    def v(self,x):
        return x+1
obj = Foo()
print(obj.v(1))     #2

 

 

2     递归--->自己调用自己

在函数中调用函数本身. 就是递归

递归的深度：自己调用自己的次数，官方文档中递归最大深度是1000，不到1000就会给你报错

 

案例：

import os
def func(filepath,n):
    #1：打开这个文件夹
    files=os.listdir(filepath)
    #2:拿到每一个文件名
    for file in files:
        #3获取到路径
        f_d=os.path.join(filepath,file) #文件的绝对路径
        #4判断是否是文件夹
        if os.path.isdir(f_d):
            #5:如果是文件夹，继续在递归
            print("\t"*n ,file,":")
            func(f_d,n+1)
        else:
            print("\t"*n,file)

func("d:",0)

3     二分查找

掐头去尾取中间. 一次砍一半

前提：必须是有序序列

 

案例：

#二分查找法
lst = [22,44,55,66,78]  #必须是有序的
n= 78
left =0
right=len(lst)-1
while left <= right:
    mid = (left + right) // 2
    if lst[mid] > n :
        right = mid -1
    if lst[mid] < n :
        left = mid+1
    if lst[mid] == n :
        print("找到了，在这个位置",mid)
        break
else:
    print("没有找到")

 

牛逼算法：----》时间复杂度：o(1)

lst1=[5,6,7,8,9]
lst2=[0,0,0,0,0,0,0,0,0,0]
for el in lst1:
    lst2[el]=1
print(lst2[5])      #结果：1

 

--->思想：想要找到一个列表中的数，把一个列表中最大的数，若是9，那么就新建一个列表长度10，若列表1的某个数存在，就把列表2中对应的位置标1，这样查询的时间复杂度位o(1),但缺点索引不能找到

 

【补充】：

1：递归算法求阶乘

li=int(input("请您输入求阶乘的数："))
fa=1
def factorial(n):
    if n >1:
        global fa
        fa = fa*n * (n-1)
        n=n-2
        factorial(n)
    return fa
print(factorial(li))

法2：
li=int(input("请您输入求阶乘的数："))
fn=1
while 1:
    fn = fn * li
    li -= 1
    if li == 0:
        break
print(fn)

2：斐波那契数列0、1、1、2、3、5、8、13、21

需求：形成斐波那契数列，并找到想要找的数的位置

li=[0,1]    #斐波那契数列
a=0         #斐波那契数列的索引
b=1            #斐波那契数列的索引
def su(n):      #递归形成斐波那契数列
    global a,b
    while b < n-1:
        li.append(li[a]+li[b])
        a += 1
        b += 1
        su(n)
        return li

def maxi(n,s):  #计算不超过某个数的最大的位置在斐波那契数列的什么位置
    if n[len(n)-1] > s:     #参数n:斐波那契数列;s:要比较的数
        for i in range(len(n)):
            if n[i]>s:
                return i-1
    else:
        return -1

co=int(input("您要多少位："))         #需要形成多少位的斐波那契数列
su(co)          #调用形成斐波那契数列
print("%s位形成的斐波那契数列是："%li)
m=int(input("请您输入不超过哪个数，我们会帮您找位置"))
c=maxi(li,m)
if c != -1:
    print("不大于%s的最大值是第%s个数"%(m,maxi(li,m)))
else :
    print(c)