三角形最小路径和（ 动态规划 leetcode ）

【题目描述】

var code = "7d05bc3a-61ee-489b-9873-4bd20d9535c3"

LRC 100.三角形最小路径和

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

示例 1：

输入：triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出：11
解释：如下面简图所示：
   2
  3 4
 6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

示例 2：

输入：triangle = [[-10]]
输出：-10

【解析】

写出三角形，题目要求当前位置（i）只能从下一行下标一样的（i）或者下标+1（i+1）这两个方向移动，如下图：

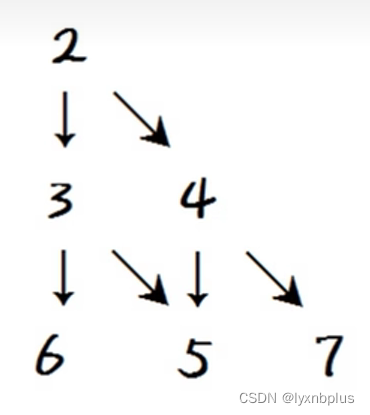
可以结点分为三种情况，当结点为每行第一个，结点为每行最后一个，结点为每行中间的。

结点为每行第一个

当前路径 = 上一行下标相同的结点的路径 + 当前结点的值

 dp[i][j] = dp[i - 1][j] + triangle[i][j]

结点为每行最后一个

当前路径 = 上一行下标减一的结点的路径 + 当前结点的值

dp[i][j] = dp[i - 1][j - 1] + triangle[i][j]

结点为每行中间的

当前路径 = （上一行下标相同的结点的路径 和 上一行下标减一的结点的路径）最小值 + 当前结点的值

dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle[i][j]

class Solution(object):
    def minimumTotal(self, triangle):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        n = len(triangle)
        dp = triangle[:] #复制triangle列表为副本
        for i in range(1, n): #第一行仅一个结点，从第二行遍历三角形
            for j in range(i + 1):
                if j == 0: #每行第一个
                    dp[i][j] = dp[i - 1][j] + triangle[i][j]
                elif j == i: #每行最后一个
                    dp[i][j] = dp[i - 1][j - 1] + triangle[i][j]
                else: #每行中间的
                    dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle[i][j]
        return min(dp[n - 1])
triangle = [[2], [3, 4],[6,5,7],[4,1,8,3]]
solution = Solution()
result = solution.minimumTotal(triangle)
print(result)