st
编译原理课程知识点
编译程序概览
编程语言基础
文法(Grammar)
如何表示文法:
•数学定义
•G=(V_N,V_T,S,P)
•V_N是非终结符号集合
•V_T是终结符号集合,可以理解为最终字符,其中有一个特殊符号ε,用于表示空
•S是初始符号
•P是产生式的集合
文法分类:
3类文法:无限制文法
对推导式左右无限制,自然语言属于这一类。
2类文法:上下文相关文法
αAβ → αγβ;这里的 A ∈ N (就是 A 是单一非终结符),α,β ∈ (N U Σ)* (就是 α 和 β 是非终结符 和终结符的字符串)而 γ ∈ (N U Σ)+ (就是 γ 是非终结符和终结符的非空字符串)。
1类文法:上下文无关文法(Context-free Grammar, CFG)
终结符号只能出现在生成式的右边;巴克斯范式(BNF)是表达它的语言
0类文法:正则文法(Regular Grammar, RG)
终结符号如果有则只能出现在生成式的右边,且只能是右侧的前缀
正则文法(0类)
正则语言:
正则表达式:各种符号代表什么: * ? + | 连接, 括号
前缀,后缀,真前缀,真后缀,真子串,子串,子序列。
有穷状态自动机(Finate Automation, FA)
数学定义
五元组
(Σ,S,s_0,δ,F)
其中,Σ是字符集(alphabet),S是状态集合(states),s_0是初始状态(initial state),δ是状态转移 函数(transition function),F是可接受状态(accepting state)的集合。
NFA与DFA
数学定义
非确定有穷状态自动机可以被定义成一个五元组
(Σ,S,s_0,δ,F)
其中,Σ是字符集(alphabet),S是状态集合(states),s_0是初始状态(initial state),δ是状态转移 函数(transition function),F是可接受状态(accepting state)的集合。
正则表达式构造有限自动机
步骤:正则式->NFA->DFA->DFA化简
1.正则式到NFA(重要)
三个转换规则 r1|r2 r1r2 r1* 如何进行画图
把其他转换规则(?, +等)都转换成上面的规则在画NFA,不确定可以多用ε链接。

2.NFA到DFA(重要)
核心思想:用NFA所有可能状态的集合作为DFA的状态
步骤:确定起始状态->构建DFA状态转移表->确定DFA接受状态
要会画表完成NFA转DFA
DFA与NFA的区别:NFA的状态转移可以有空串,即可以用ε链接状态。
一个状态的集合就是其通过空串链接的所有状态。
终态就是状态集合里面包含结束状态。
3.DFA化简(最小DFA)
把DFA的终态集合和不含终态集合分别进行化简运算,化完即为最小DFA(有可能NFA转完就是最小DFA,不能化简)
看集合经过一个a或者一个b的状态集合是否是集合的子集,是就可以进行合并。
泵引理
这个理论用来证明某些语言不是正则语言/上下文无关语言
L 是正则语言,则存在整数 n ≥ 1 使得任意长度超过 n 的字符串 w 都可以被改写成
xyz 的形式并满足:
1 |xy| ≤ n;
2 |y| ≥ 1;
3 ∀k ≥ 0 : x y^k z ∈ L。
L 是上下文无关语言,则存在整数 n ≥ 1 使得任意长度超过 n 的字符串 w 都可以被改
写成 uvxyz 的形式并满足:
1 |vxy| ≤ n;
2 |vy| ≥ 1;
3 ∀k ≥ 0 : uvkxykz ∈ L。
上下文无关文法(CFL)
上下文无关语言:
下推自动机(Pushdown Automation PDA)
定义:•PDA可以被定义为下面的六元组
M=(Q,Σ,Γ,δ,q_0,F)
•Q是所有状态的集合,有限个
•Σ是输入字符的集合,有限。特别地,Σ_ε={ε}∪Σ
•Γ是栈字符的集合,有限。特别地,Γ_ε={ε}∪Γ
•δ是转移函数
δ:Q×Σ_ε×Γ_ε→Q×Γ_ε
•根据输入和当前栈顶元素进行转移的同时替换栈顶元素
•特别地,转移函数支持ε作为栈顶元素,也支持将栈顶元素替换为ε。这两个操作一个是单纯压 栈,另一个是单纯弹栈
q_0, F的意思和NFA中的一致
定理与引理
最左推导与最右推导
•最左推导(Leftmost derivation)
首先替换最左边的非终结符
•最右推导(Rightmost derivation)
首先替换最右边的非终结符
二义性分析:对于某一个串存在至少两个不同的最左/右推导来证明
要对有二义性的文法进行改写
语法分析树的结构与使用最左推导还是最右推导无关
巴克斯范式(BNF)
是一种用于表示上下文无关文法的语言
<符号> ::= <使用符号的表达式>
<符号> 是非终结符
表达式由
一个符号序列
或用竖杠 '|' 分隔的多个符号序列构成
每个符号序列整体都是左端的符号的一种可能的替代
从未在左端出现的符号叫做终结符
语法树构建
具体的知识点在语法分析展开
自顶向下(Top-Down)
开始符号出发,反复使用产生式:左部符号替换成右部
树根开始构建语法树
递归下降分析法,预测分析法
自底向上(Bottom-Up)
从输入串开始归约;
归约:根据文法的产生式规则,把串中出现的产生式的右部替换成左部符号
树叶节点开始,构建语法树
算符优先分析法,LR分析法
词法分析
语法分析
语法分析最坏时间复杂度:O(n3)
自顶向下
递归下降
消左递归
直接左递归:
非终结符 -> 非终结符
例如: E-> E|T
间接左递归:
非终结符间接推出本身
例如: E-> T ; T -> F ; F -> E
如何消除:A -> Aab
改为: A -> b A'
A' -> aA' | ε
提取左公因式(回溯)
非终结符的匹配可能是暂时的,出错时要回溯,比如说同一个非终结符的多个候选式存在共同前缀。
例如: A -> aABb | a
提取后为: A -> aA' | b
A‘ -> AB | ε
预测分析法
First集与Follow 集
是两个文法相关的函数。
在自顶向下与自底向上的分析器构造中都会用到。
对于非终结符号 A,FOLLOW 被定义为可能在某些句型中紧跟在 A 右边的终
结符号的集合
特别地,如果 A 是某些句型最右的符号,则 $ ∈ FOLLOW(A) 表示输
入的终止(EOF)。
First集很好计算
Follow集三条规律:
将 $ 放到 FOLLOW(S) 中;
如果存在一个产生式 A → αBβ,则 FIRST(β) 中除了 ϵ 以外的符号都在 FOLLOW(B) 中;
如果存在一个产生式 A → αB,或存在 A → αBβ ∧ ε ∈ FIRST(β),FOLLOW(A) 所有符号都在 FOLLOW(B) 中;
predict集合:
LL(1)文法![img]()
是一类特别的上下文无关文法。
第一个 L 表示“Left-to-Right”,即从左往右扫描;
第二个 L 表示“Leftmost”,即最左推导;
(1) 表示每次推导只需要看一个输入符号就可以决定语法分析动作,即决定使用
那个推导式。
满足LL(1)文法的条件:
文法 G 是 LL(1) 文法当且仅当 G 的任意两个不同的产生式 A → α|β 满足下列
条件
1 不存在终结符号 a 使 α 和 β 都能推导出以 a 开头的串。
2 α、β 中最多一个可以推导出空串 ε。上面两个条件等价于 FIRST(α) ∩ FIRST(β) = ∅)
3 若 β ⇒⋆ ε,则 α 不能推导出任何以 FOLLOW(A) 中某个终结符开头的串。反之亦然。
(ε ∈ FIRST(β) → FIRST(α) ∩ FOLLOW(A) = ∅)
表驱动的预测分析法
由下推栈,预测分析表,控制程序组成,是一种确定性的下推自动机
过程: 先消除左循环和提取做公因式
再得出其first集和follow集
再构造LL(1)预测分析表
Input: P, FIRST(·), FOLLOW(·)
for A → α ∈ P do
if a ∈ FIRST(α) then
M[A, a] ← (A → α);
end
if ε ∈ FIRST(α) then
for b ∈ FOLLOW(A) do
M[A, b] ← (A → ε);
end
end
end
如果一个格子里面有多于 1 条规则,不是 LL(1) 文法,返回错误;
预测分析法如何检测错误?
栈顶的终结符号与输入不匹配;
栈顶的非终结符号 A,但 M[A, a] = error。
如何处理错误?
恐慌模式,短语恢复
自底向上
归约与移入
定义:先将一个子串与某规则的右部匹配,然后将该子串替换为该规则的左部
移入-归约框架:
在对输入串的一次从左到右扫描过程中,语法分析器将零个或多个输入符号移入到栈的顶端,直到它可以对栈顶的一个文法符号串 β(可归约符号串) 进行归约为止;然后,它将 β 归约为某个产生式的左部;不断地重复这个循环,知道检测到语法错误或者栈中包含开始符号且输入缓冲区为空。
短语,句柄,前缀
对于文法 G(S),αβδ 是 G 的一个句型。如果有 S ⇒⋆rm αAδ, 且
• A ⇒+rm β,则称 β 是句型 αβδ 相对于 A 的短语。
• A ⇒rm β,则称 β 是句型 αβδ 相对于 A 的直接短语(简单短语)。
• 一个句型的最左直接短语称为该句型的句柄(Handle)。
⇒:单步推导
⇒*:零步或多步推导
⇒+:多步推导
要会通过构建语法树来判断短语,句柄,直接短语。
在一个句型的语法树中:
•任一子树的叶节点从左到右排列所组成的符号串都是该句型的短语。
• 任一最小子树(树高?为 1)的叶节点所组成的符号串都是该句型的直接短语。
• 句柄是最左边的直接短语。
规范句型
规范归约 ≡ 最左规约:在自底向上的分析中,总是采用最左归约的方式,因此把最左归约称为规范归约
规范推导 ≡ 规范推导:规范归约是最右推导的逆过程,则最右推导相应地称为规范推导。
规范句型:由规范推导推出的句型称为规范句型。
前缀与各种缀
前缀:符号串的任意首部。
活前缀:文法 G(S) 的一个规范句型 αβ,其中 β 为终结符号串。若 α 不含句柄之后的任何符号,则称 α 为活前缀(可行前缀)。
可归前缀:如果 α 是含有句柄的活前缀,则称 α 为可归前缀。
可归前缀即最长的活前缀。
移入-归约冲突
即使知道所有栈内符号和后续的 k 个符号,也无法判断应将新元素移入栈还是将栈中已有元素进行归约。
归约-归约冲突
即使知道了所有栈内符号和后续的 k 个符号,无法判断用哪个产生式归约。
LR(0)
项,项集闭包,项集族
先构建拓广文法->构项集闭包,项集族I->根据项集族来写分析表(ACTION, GOTO)
局限性:移入-归约冲突,归约-归约冲突
LR(0)自动机是DFA。
五元组对应:
| 构成要件 | DFA | LR(0) 自动机 |
|---|---|---|
| 字符集 | Σ | 文法符号(含终结符和非终结符) |
| 状态 | q | 一个项集的闭包 |
| 有限的状态集合 | Q | 规范 LR(0) 项集族 |
| 状态转移函数 | δ(q, a) | GOTO 函数 |
| 起始状态 | q0 | CLOSURE({[S′ → ·S]}) |
| 接受状态集合 | F | 包含项 [S′ → S·] 的项集对应 $ 输入时的状态 |
分析表构造:
令 Ii 对应状态 i,则 ACTION 表和 GOTO 表构造如下:
• (A → α · aβ ∈ Ii ∧ GOTO(Ii, a) = Ij) −→ ACTION[i, a] = sj;
• (A → α · Bβ ∈ Ii ∧ GOTO(Ii, B) = Ij) −→ GOTO[i, B] = sj;
• (A → α· ∈ Ii ∧ A̸ = S′) =⇒ ∀a ∈ VT ∪ {$ }ACTION[i, a] = rj,其中 j 是产生式A → α 的编号;
• (S′ → S· ∈ Ii) =⇒ ACTION[i, $] = acc;
• 没有定义的所有条目都设置为“error”。
SLR(1)
使用FOLLOW集合来尝试解决LR(0)存在的冲突,注意:尝试解决任然可能出现冲突
移进项目终结符和归约项目的FOLLOW集判断是否有交集,有就不是SLR(1)文法
LR(1)
使用向前搜索符
移进项目终结符和归约项目的向前搜索符判断是否有交集,有就不是LR(1)文法
LALR(1)
合并同心项(表达式相同,向前)
四种文法的对比与区别
| 步骤 | LR(0) | SLR(1) | LR(1) | LALR(1) |
|---|---|---|---|---|
| 构建增广文法 | ✓ | ✓ | ✓ | ✓ |
| 对所有规则编号 | ✓ | ✓ | ✓ | ✓ |
| 求非终结符的 FOLLOW 集 | ✓ | |||
| 求非终结符的 FIRST 集 | ✓ | ✓ | ||
| 构建 LR(0) 项集族 | ✓ | ✓ | ||
| 构建 LR(1) 项集族 | ✓ | ✓ | ||
| 合并同心集 | ✓ | |||
| 根据项集族构建分析表 | ✓ | ✓ | ✓ | ✓ |
归约项目 A -> a· 点在最后
接受项目 S -> a· 开始文法对应(一定有一个)
移进项目 A -> a · x β 点后x是终结符
待约项目 A -> a · x β 点后x是非终结符
LR(0)文法:不存在冲突项目(移进-归约, 归约-归约)
SLR(1)文法:存在冲突项目(移进-归约)
LR(1)文法:存在冲突项目(移进-归约, 归约-归约)
LALR(1)文法:合并同心集后无归约-归约冲突
同心集合并不会产生移进-归约冲突,但可能产生归约-归约冲突
LR(0) < SLR(1) < LR(1) < LALR(1)
语义分析
三目标:静态语义检查,构建符号表,为中间代码生成或优化提供语义信息
核心任务;类型检查,作用域分析,一致性检查,控制流验证,符号表管理
管理键值对:数据结构:二叉查找树,哈希表,
管理作用域:理想:可持久化数据结构
现实:顶层浅拷贝,记录新增和变化,离开时还原。
类型检查:意义:确保操作符,表达式和赋值等行为符合语言类型系统的约束,
避免因类型不匹配导致的逻辑错误或者运行时崩溃
方法:静态语义分析遍历抽象语法树
语法制导翻译
基本概念
定义:语法制导翻译使用上下文无关文法 CFG(context free grammar)来引导对语言的翻译,是一种面向文法的翻译技术。
阶段:横跨了语法分析、语义分析、中间代码生成三个阶段。
基本思想:归约到某个产生式,除了按照产生式进行相应的代换之外(语法分析),还要按照产生式所对应的语义规则执行相应的语义动作,如计算表达式的值、产生中间代码(语义分析)。
表示语义信息:为CFG的文法符号设施语义属性,
计算语义属性:输入串X,构建X的语法分析树,利用语义规则来计算分析树中对应文法符号的语义属性值
对输入串的翻译就是根据语义规则进行属性计算。
语义规则也叫语义子程序或语义动作。
语义与语法联系起来的方式:
语法制导定义(Syntax-Directed Definitions,SDD)
语法制导翻译方案(Syntax-Directed Translation Scheme,SDT)
语法制导定义(Syntax-Directed Definitions,SDD)
SDD 是对 CFG 的推广
计算综合属性和继承属性
- 综合属性用于“自下而上”传递信息,通过分析树中其子节点的属性值计算出来。
- 继承属性用于“自上而下”传递信息,由该节点的兄弟节点及父节点的属性值计算出来。
终结符没有继承属性,可以有综合属性
画依赖图
S-SDD
仅仅使用综合属性的 SDD 称为S属性的 SDD,或S-属性定义、S-SDD。
如果一个 SDD 是 S 属性的,可以按照语法分析树节点的任何自底向上顺序来计算它的各个属性值。
S-属性定义可以在自底向上的语法分析过程中实现。
L-SDD
L-属性定义(也称为 L 属性的 SDD 或 L-SDD)的直观含义:在一个产生式所关联的各属性之间,依赖图的边可以从左到右,但不能从右到左(因此取 Left的首字母,称为 L 属性)。
一个 SDD 是 L-属性定义,当且仅当3它的每个属性要么是一个综合属性,要么是满足如下条件的继承属性:假设存在一个产生式 A → X1X2 . . . Xn,其右部符号 Xi(1 ≤ i ≤ n) 的继承属性仅依赖于下列属性:
• A 的继承属性;
• 产生式中 Xi 左边的符号 X1, X2, . . . , Xi−1 的属性;
• Xi 本身的属性,但 Xi 的全部属性不能在依赖图中形成环路。
• 特别地,每个 S-属性定义都是 L-属性定义。
语法制导翻译方案(Syntax-Directed Translation Scheme,SDT)
语法制导翻译方案(SDT)是 SDD 的补充,它给出了语义规则计算的次序,把实现细节表示出来。
合适位置嵌入了程序片段,在语法分析的同时执行这些语义动作
SDT 的设计原则:保证语义动作不会引用还没有计算的属性值。
• L-属性定义:本身就能确保每个动作不会引用尚未计算出来的属性。
• S-属性定义:为每一个语义规则建立一个包含赋值的动作,并把这个动作放在相应的产生式右边的末尾。
S-SDT:
S-属性定义:只包含综合属性。
• 综合属性可以在分析输入符号串的同时,由自下而上的分析器来计算:
• 分析栈中保存文法符号和有关的综合属性值;
• 每当进行归约时,新的语法符号的属性值就由栈中正在归约的产生式右边符号的属性值来计算。
为每一个语义规则建立一个包含赋值的动作,并把这个动作放在相应的产生式右边的末尾。当按照该产生式进行归约时,执行这个动作。
L-SDT:
L-属性定义:包含综合属性和特殊的继承属性。
• 产生式右边的符号的继承属性必须在这个符号以前的动作中计算出来。
• 一个动作不能引用这个动作右边符号的综合属性。
• 产生式左边非终结符号的综合属性只有在它所引用的所有属性都计算出来以后才能计算。计算这种属性的动作应放在产生式右端的末尾。
• 转换规则:
• 将计算某个非终结符号 A 的继承属性的动作插入到产生式右部中紧靠在 A 的本次出现前的位置上;
• 将计算一个产生式左部符号的综合属性的动作放置在这个产生式右部的最右端。
自顶向下翻译
消除左递归
递归下降分析器
A 的每个继承属性对应函数 A 的一个形式参数;
函数 A 的返回值为 A 的综合属性值;
中间代码生成
定义:中间代码是源程序在编译过程中的一种中间表示(Intermediate Representation,IR)形式
特征:中间代码介于高级语言与机器码之间,具有结构简单、机器无关性强的特征。
目的:引入中间代码的核心目的是增强编译器的可移植性,并为代码优化提供结构化支持。
必要性:可移植性,代码优化,开发维护
逆波兰表达式(后缀表达式)与四元式
三地址码
三地址码既可以是树形 IR(如 AST)的线性表示,也可以是 DAG 的线性表示。
三地址码说明了各类指令的组成部分,但未描述指令在某个数据结构中的表示方法。它可以用四元式、三元式和间接三元式来描述。
四元式:(运算符, 操作数 1, 操作数 2, 结果)
三元式:三元式是 3 个字段的记录结构:op, arg1, arg2;
不引入临时变量;
使用运算 x op y 来引用其运算结果;
使用带有括号的数字表示指向三元式结构的指针。
间接三元式:三元式表 + 间接码表
间接码表:一张指示器表,按运算的先后次序列出有关三元式在三元式表中的位置,优化编译器可以通过对该表的重新排序来移动指令的位置。从0开始
优点:方便优化,节省空间
中间代码生成策略
输入:经过语法分析与语义分析的抽象语法树或符号表。
输出:与目标机器无关的三地址码、四元式或其他中间形式。
关键步骤:
• 声明处理:将变量类型、作用域等信息登记至符号表,分配存储地址(如相对偏移量)。
• 表达式翻译:递归遍历语法树,生成运算序列(如利用语法制导翻译生成四元式)。
• 控制结构处理:为条件语句、循环语句生成跳转指令标签。
优化技术:
• 常量传播:替换编译时可确定的常量值。
• 死代码消除:删除不可达或无效代码段。
• 公共子表达式提取:重用重复计算的中间结果。

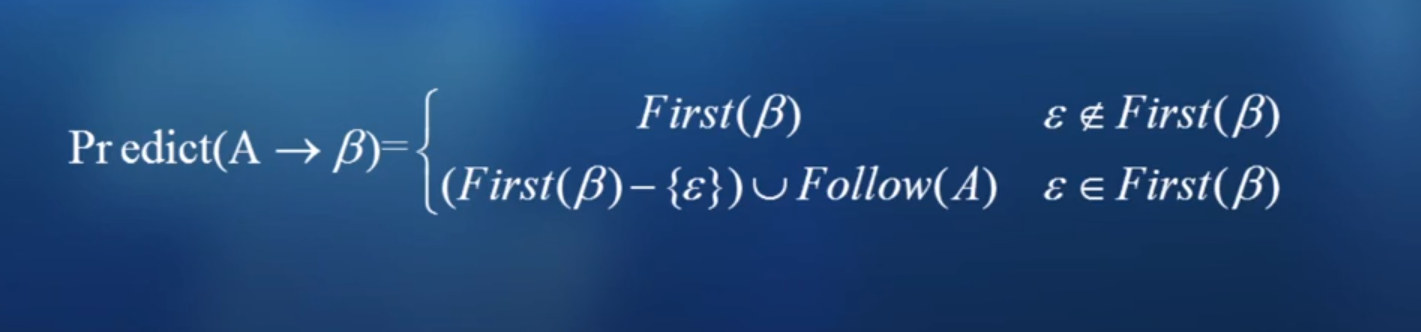


 浙公网安备 33010602011771号
浙公网安备 33010602011771号