E - Road Reduction -- BFS & Dijkstra

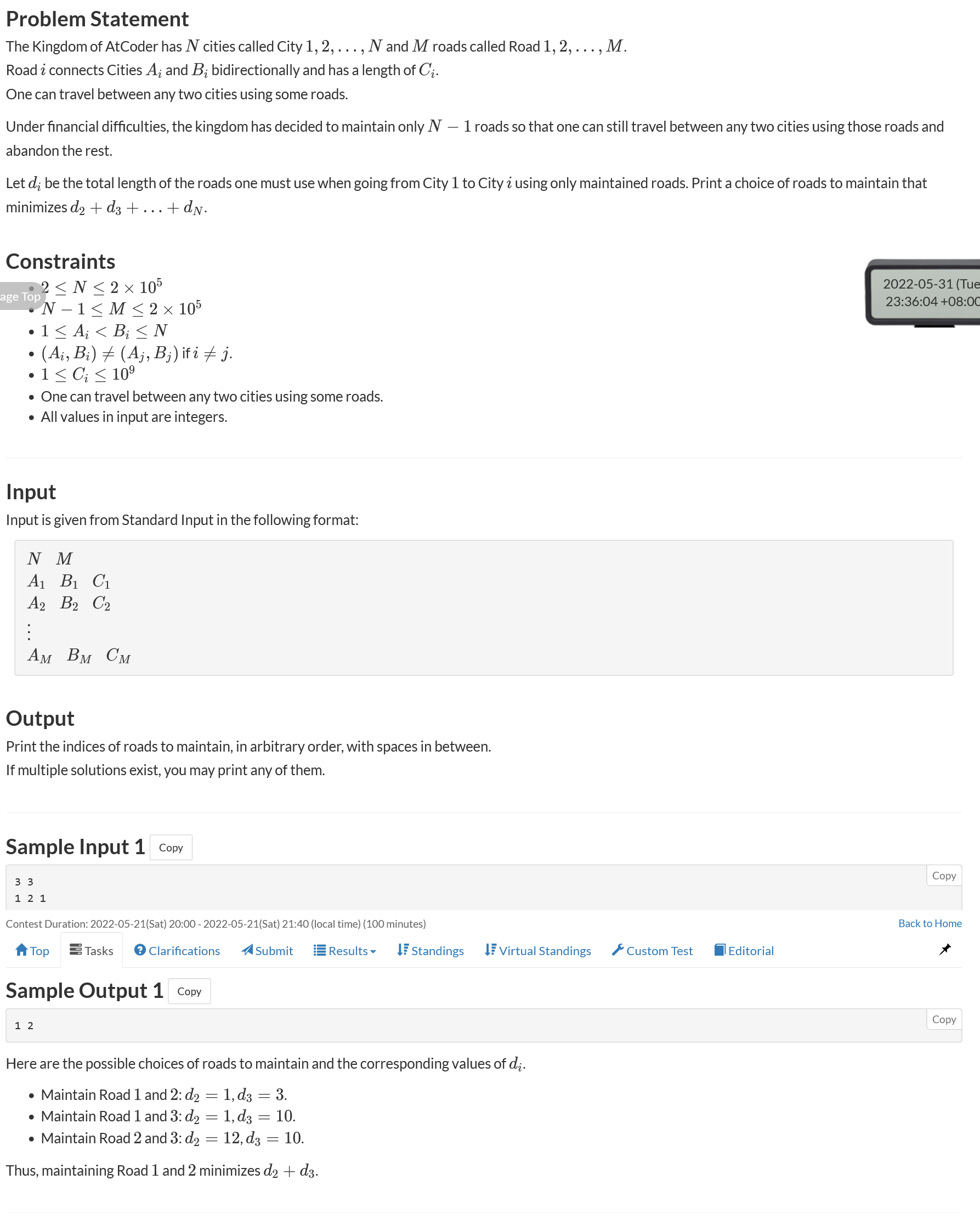
E - Road Reduction

https://atcoder.jp/contests/abc252/tasks/abc252_e

思路

https://www.cnblogs.com/zengzk/p/16296821.html

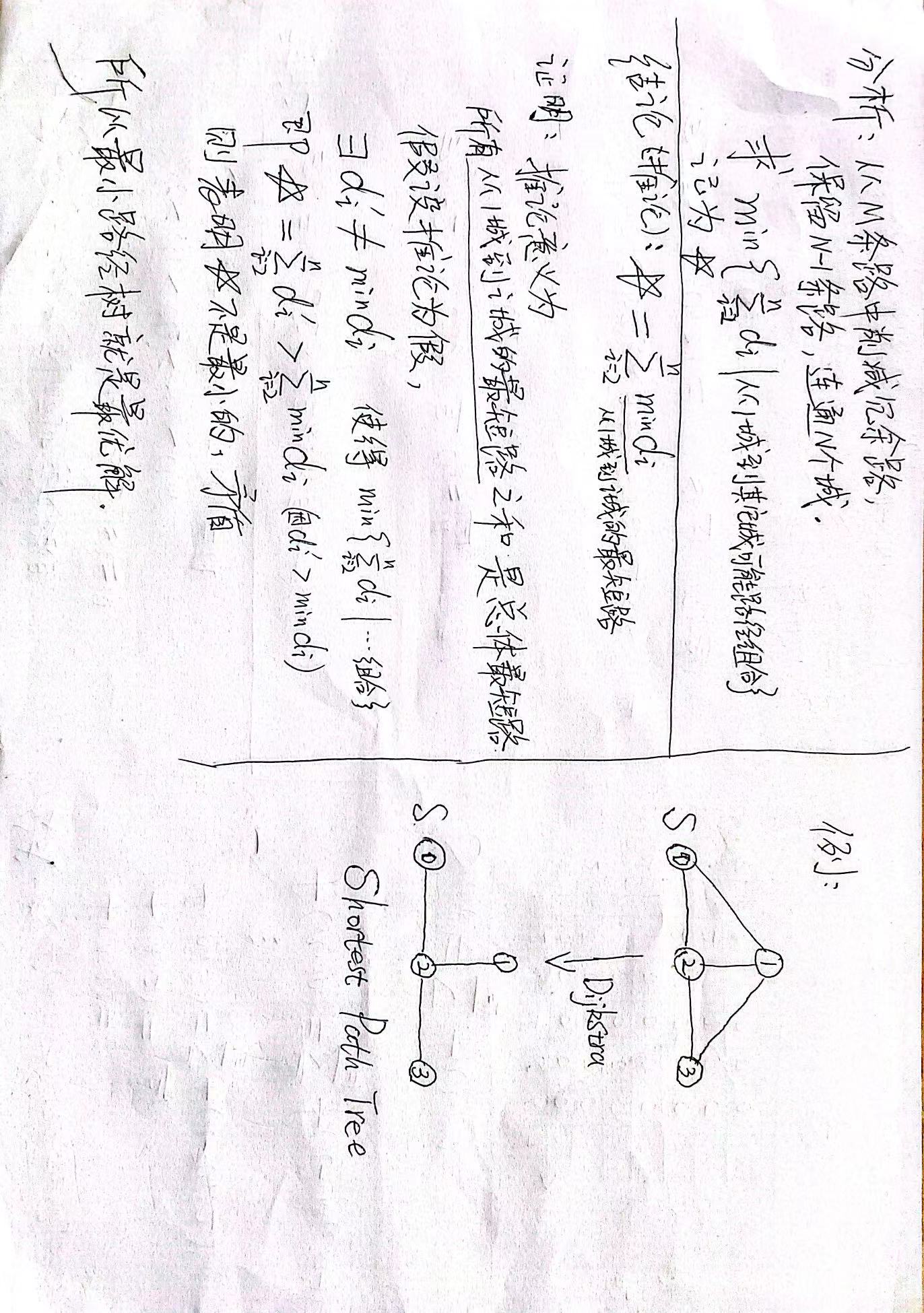
一眼最短路树，跑遍dijkstra就行了。

 

分析：

要求从某个起点到所有节点的路径之和是最小的，最短路算法给出的路径选择，就是最优解。

 

 

Code

// A C++ program for Dijkstra's single source shortest path algorithm.
// The program is for adjacency matrix representation of the graph
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
#include <limits.h>


/*
https://atcoder.jp/contests/abc252/tasks/abc252_e
https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-greedy-algo-7/
*/

class Node {
    public:
        int index; // vertex index  in graph
        int64_t dist; // distance from source point
        int prev_index; // from which vertex the dist was calculated

    public:
        Node(int _index, int64_t _dist, int _prev_index) {
            index = _index;
            dist = _dist;
            prev_index = _prev_index;
        }

        bool operator<(const Node &nd) const {
            if (dist < nd.dist) {
                return true;
            }

            return false;
        }

        bool operator>(const Node &nd) const {
            if (dist > nd.dist) {
                return true;
            }

            return false;
        }
};


int N, M;
map<int, map<int, int64_t>> graph;
map<int, map<int, int>> road_number;

// A utility function to print the constructed distance array
void printSolution(vector<int64_t> &dist, set<int> &road_used) {
//    cout << "Vertex \t Distance from Source" << endl;
//    for (int i = 1; i <= N; i++)
//        cout << i << " \t\t" << dist[i] << endl;
//
//    cout << "Road used:" << endl;
    set<int>::iterator it;
    for (it = road_used.begin(); it != road_used.end(); it++) {
        cout << *it << " ";
    }
}


// Function that implements Dijkstra's single source shortest path algorithm
// for a graph represented using adjacency matrix representation
void dijkstra(int src) {
    vector<int64_t> dist(N + 3, INT64_MAX); // The output array. dist[i] will hold the shortest
    // distance from src to i

    // smallest on head, for watch connected directly vertexes from close set
    priority_queue<Node, vector<Node>, greater<Node>> open_pq;

    // sptSet[i] will be true if vertex i is included in shortest
    // path tree or shortest distance from src to i is finalized
    set<int> close_set;

    set<int> road_used;

    // Distance of source vertex from itself is always 0
    dist[src] = 0;
    open_pq.push(Node(src, 0, -1));

    // Find shortest path for all vertices
    while (!open_pq.empty()) {
        // Pick the minimum distance vertex from the set of vertices not
        // yet processed. u is always equal to src in the first iteration.
        class Node nd = open_pq.top();
        open_pq.pop();

        int u = nd.index;

        // if u is already in spt, skip
        if (close_set.find(u) != close_set.end()) {
            continue;
        }

        // Mark the picked vertex as processed
        close_set.insert(u);

        // mark road_used
        int prev_index = nd.prev_index;
//        cout << "u =" << u << " prev_index=" << prev_index << endl;
        if (-1 != prev_index) {
            int road_index = road_number[prev_index][u];
//            cout << "road is been used. -- " << road_index << endl;
            road_used.insert(road_index);
        }

        // Update dist value of the adjacent vertices of the picked vertex.
        for (auto [v, w] : graph[u]) {

            // Update dist[v] only if is not in sptSet, there is an edge from
            // u to v, and total weight of path from src to v through u is
            // smaller than current value of dist[v]
            if (close_set.count(v) == 0 && w && dist[u] != INT64_MAX
                    && dist[u] + w < dist[v]) {
                dist[v] = dist[u] + w;
                open_pq.push(Node(v, dist[v], u));
            }
        }
    }

    // print the constructed distance array
    printSolution(dist, road_used);
}


// driver program to test above function
int main() {
    cin >> N >> M;

    for (int i = 1; i <= M; i++) {
        int a, b, c;

        cin >> a >> b >> c;

        /*
        graph index:
            row: 1->N
            column: 1->N
        road_number:
            value: 1 -> M
        */
        graph[a][b] = c;
        graph[b][a] = c;
        road_number[a][b] = i;
        road_number[b][a] = i;
    }

    dijkstra(1);

    return 0;
}