《机器学习基石》笔记整理(1)
Table of Contents
https://blog.csdn.net/qq_34993631/article/details/79320847
力荐 | 台大林轩田《机器学习基石》资源汇总
https://blog.csdn.net/red_stone1/article/details/80044059
林轩田机器学习课程笔记
https://blog.csdn.net/column/details/23475.html
机器学习
https://blog.csdn.net/column/details/17699.html
数字图像处理
https://blog.csdn.net/column/details/14330.html?&page=1
人工智能实战
https://blog.csdn.net/column/details/24104.html
coursera-斯坦福-机器学习-吴恩达-第1周笔记
https://blog.csdn.net/u012052268/article/details/78555392
PLA算法
PLA算法的机制
故事起源于一个二元分类问题(比如说银行要不要给客户发信用卡的问题)
我们的先决条件
1.我们有资料在手上(用户信息)
2.我们的资料有标签(有没有发信用卡)
3.假设我们的资料是线性可分的(可以被一个超平面所分割)
我们的假设
我们首先要给每一笔资料算出一个得分函数,由于资料是线性可分的所以我们有如下假设
其中threshold为我们规定的门槛值,当得分为正sign()的结果为+1我们会给该客户发信用卡,否则不会。在此为了运算上的方便我们把门槛值归并到第0维中。
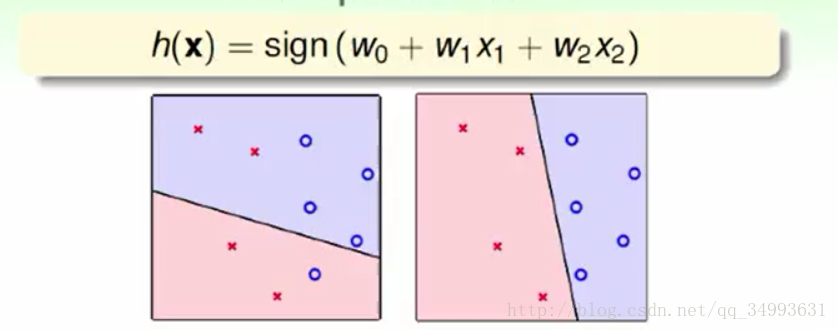
假设我们的得分函数是二维的,则h(x)的几何意义如下:
在这两幅图中每一个点代表一个用户(对应的资料),x与o代表没有发信用卡与发了信用卡,而图中的线(在高维空间中就是超平面)就是h(x)所代表的几何意义,它的作用是将平面分成两份。而进一步说h(x)的集合(假设集合)就是图中的无限多条线。我们的目的是利用学习算法找到一条能够完全正确的分割资料的直线。
PLA算法登场
基本描述:
1.首先我们有一条随机的直线在手上。
2.我们将遍历所有的资料,将所有的资料带入上面的假设。比较计算的结果与实际的标签是否对应。对于犯错误的点我们就要更新手上的直线。
3.更新直线让它离我们理想的直线越来越近。
在遇到犯错误的点是我们使用如下的公式来进行更新
它的底层逻辑基于向量的内积(两个向量的内积越大那么他们的相关性越强),如果预测y为+1实际为-1那么就将w与x的夹角往大调,如果预测y为-1实际为+1那么就将w与x的夹角往小调。归结起来就是上面的(2)式(其中y为实际的标签值)。就这样一个知错能改的算法在跑若干轮后就能够得到我们想要的直线。
PLA算法有效性的证明
我们的思路是证明我们每一轮的更新都会接近与我们理想中的那条线,具体来说就是求出他们的标准化的内积会越来越大。
https://blog.csdn.net/qq_34993631/article/details/79189543
PLA算法的不足
我们在不知道数据的情况下(是否线性可分)PLA就不会停下来,这个时候我们会使用Pocket演算法来找到一根不错的直线。Pocket演算法的基本思想就是找到一根犯错误更小的直线。实务上我们一般会执行到一定的时间或者一定的步数就会停下来。结果是它是一条不错的线,但是可能不是一个最优解。
VC维度
https://blog.csdn.net/qq_34993631/article/details/79200782
一个小问题引出的大思考
我们首先玩一个简单的找规律游戏
2 , 4 ......
请问第三个数是多少,6? 8? 5?又或者是其它。假如我是一个命题人你的回答可能都对又可能都错。因为满足这样的规律事实上是有无穷个而不能想当然。看来机器学习在这个小的数据集上面跑是无法学到东西,无法做出预测的。就算是这道题的包装也可能只是规律更加复杂了,这样的题严格的来说是没有答案或者有无数答案。
借助自然界的力量
自然界中老是潜藏着一些规律,我们在一个装有黑白两种颜色的罐子中随机抓一把出来。我们手中的黑白的比例大概差不多就是罐子中所有的黑白的球的比例,而且我们抓的资料越多比例就会越接近,这也是大数定理的一个很好的体现。而数学家Hoffding将这个过程进行了量化的处理得出了Hoffding`s Inequality (霍夫丁不等式)。
在这个式子中v是样本的各个球的比例,μ是总体球的比例。他们之间的差距会随着右边的数据量N的变大而缩小。(ε为容错量它是一个常数)这个式子直观的说明在数据量足够的情况下我们样本中的分布与整体上数据的分布式大概差不多是相等的(及著名的Probably Approximately Correct 大概差不多是对的)。这是所有机器学习的基本保障。
与机器学习的联系
假设我们的理想模型是f(x)它产生了所有的数据,我们对于现象的假设为h(x)。
我们在我们的样本(独立随机抽样以保证样本与总体数据的分布统一)中给小球进行着色,着色的规则是对于某一个小球,h(x)在该小球上的预测与f(x)预测的相同时,图成绿色,否则图成橘色。这样一来橘色的比例就是我们的模型h(x)在样本上犯错误的比例我们称之为Ein,而在h(x)在总体数据集上所犯的错误是Eout。
在数据量的保障下与随机独立抽样的条件下,我们的h(x)在样本上的错误率大概差不多等于在总体数据上的错误率。及Ein ≈Eout。看来我们能够评判一个模型的好坏。
自由选择的代价
在上面的论述中我们做的是对一个给定的模型我们检测它的表现如何。而真正的机器学习不是单看一个模型的好坏而是要选择一个尽可能最优的结果。所以我们要加上选择的过程。让学习算法去选择更好的h(x)吧。
什么是坏的资料?
在机器学习中我们把与总体数据的分布不同的样本称之为坏的资料。假如说我们有一个模型很顺应这个坏的资料(在坏的资料上的Ein ≈ 0),殊不知自己只是在样本上做的不错而与实际的总体数据格格不入这样的模型我们就称之为坏的模型。但是这些坏的资料会干扰我们的选择,会让我们有很大的几率选择到坏的模型看样子我们的学习遇到了困难。
如何避免坏的资料
但从直觉上来说,一笔坏的资料对于任何一个h(x)来说都是一件坏的事情。也就是说如果一个h(x)遇到坏资料的概率是Pd,则m个h(x)遇到的坏资料的概率就是m*Pd。霍夫丁不等式的保证如下:
很显然我们可以通过提高我们的数据量来降低我们遇到坏资料的概率。在数据量的保证下看样子我们能够学到东西。
危机再现无限多个h(x)的困境
在实务上我们的h(x)是有无限多种选择的就像是一个线性二分的例子中能存在的超平面有无限多个,所以看起来我们的资料量在大也无济于事。
无限多个h(x)的条件下ML可行性的证明
首先我们再次明确目的Eout≈Ein ≈0
Ein ≈ 0,由学习算法来保障,Eout≈Ein需要的是样本与总体数据的分布相同(也就是避免坏的资料)与霍夫丁不等式。
我们接下来讨论的就是如何避免坏的资料。
……
VC维度的提出
VC维度的意义
1.VC维度可以代表假设集合的复杂程度,这也是我们引出VC维度的初衷(我们试图解决h(x)集合太大给我们带来的坏资料的问题)。VC维度越大,一个假设集合大小的上限函数就会增加假设集合的复杂程度会增大。
2.VC维度还可以代表假设本身的复杂性,简单的例子就是我们的VC维度越高如2D的perceptrons的dvc==3而假设我们将VC维度上调为4的时候我们就能得到4个点的完全二分的集合。我们能够做出更为复杂的分割动作,也就是我们的单个模型拥有更为强大的分割能力!
综上所述我们的假设集合与单个假设的复杂度都会随着VC维度的增加而增加从而变得更加的强大。
强大的不一定是好的
我们将以上含有VC维度的霍夫丁不等式中的各个变量进行整合会得到以下的结论与曲线:
其中Ω代表我们的模型复杂度。看图我们会发现:随着VC维度的增大Ein会变得低但是ΩΩ会变得高,随着VC维度的降低Ein会变高而Ω会变得低。围绕我们的目标Eout≈Ein ≈0我们会发现我们要的最优解并不是VC维度很高的时候,而是某一个中间的地方。
VC维度在实际中的保障
在实务上我们想要训练出一个不错的模型,在理论上我们需要10000*dvc笔资料,但是经验告诉我们只需要10*dvc笔资料我们就会得到不错的结果。核心的原因就是VC上限是一个非常宽松的上限。具体体现在如下4个方面:
1.霍夫丁不等式无需关注总体数据的分布。
2.我们在实务上需要的是有效的h(x)而非所有的h(x)。
3.在有限的VC维度下我们有效的h(x)个数会被一个多项式所限制住N^dvc(事实上是上限的上限)。
4.在多个h(x)的情况下,我们遇到坏的资料的概率并非是累加的而是重叠的。
噪音
noise的产生
在机器学习中我们在独立随机抽样的时候会出现一些搞错的信息,这些错误的数据我们称之为杂讯(或者噪音 noise),一般可以归结为一下两种(以二分为例):
输出错误:1.同样的一笔数据会出现两种不同的评判 2.在同样的评判下会有不同的后续处理。
输入错误:1.在收集数据的时由于数据源的随机性会出现错误(比如说,客户在填信息的时候出现的误填)
noise的情况下VC维度的可用性
在有noise的情况下我们的资料不会都来自于我们所求的目标函数而是来自于一个带有noise的分布,因此我们的f(x)会在产生资料的时候加上一个波动值后变成了f(x)+noise它具有一定的随机性。
在这里需要注意的是我们的资料产生于一个带有noise的分布,而我们预测的资料也是产生于一个同样的分布。直观的来看只是一个换了分布的机器学习过程。所以VC维度能够在有杂讯的情况下学习,所有的论述过程同这篇文章机器学习与VC维度。
noise的代价
我们能够在有杂讯的资料上学习,通过一个带有杂讯的分布,当然我们会犯错。在遇到一个具体的点的时候,我们会查找这个点在我们的标签分布上的概率p(y | x),比如说这个分布会告诉我们x的概率为0.7,o的概率是0.3,那么我们就会选择概率较大的那个选项,但是我们有0.3的几率会犯错,这就是我们的代价。
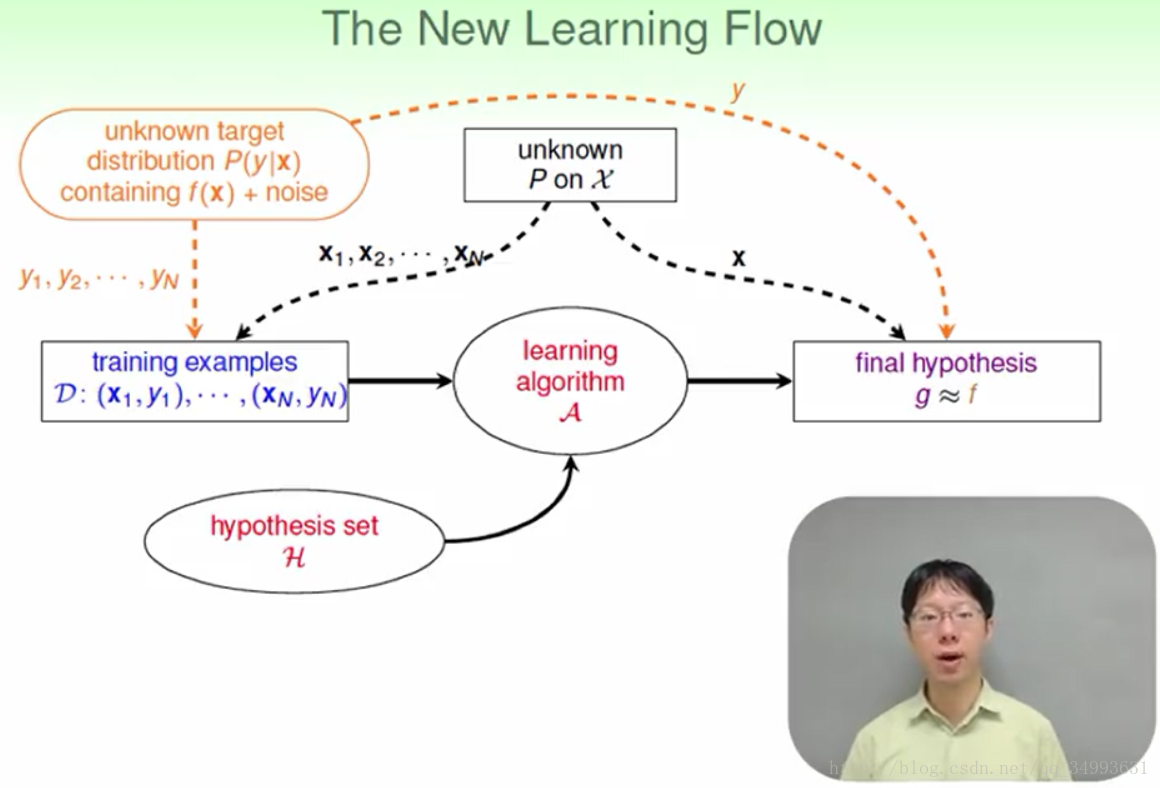
修正后的机器学习模型图如下:
错误衡量
为什么有个错误衡量
在看完周志华老师《机器学习》中的归纳偏好中有这样的描述:归纳偏好就是要做出学习算法本身“什么样的模型更好”的假设。在这里我们要给模型的好坏下一个定义如果算法A比算法B好,那么一定要定义什么是好。在没有定义什么是好之前我们无法找到我们的模型要训练的方向。那么反过来当我们遇到错误的时候我们就要给错误下一个定义。
举一个例子,在战争时期我打死一个敌人对于我方来说是一件好事(正确),但在敌方来看这就是一件坏事(错误)。所以我们就要针对不同的问题提出不同的错误衡量来使得算法趋向于我们想要的方向。
一个错误衡量的实例
在以下的案例中我们的数据完全一样,但是因为有了错误衡量所以我们就有了两种完全不同的结果
在接下来我们会用两种不同的错误衡量来选择出最佳结果,如上图所示我们使用的是平均错误与平方错误
从图中我们可以看出在平均错误的情况下我们得到的最好的结果是2因为(错误率为0.3)最坏的结果为1.9(错误率为1),而在平方错误下我们的最优结果是1.9(错误率为0.29)而最差的结果为3(错误率为1.5)。这就是错误衡量的力量。(平方错误的计算方法为‘以1为例’(2-1)^2*0.7+(3-1)^2*0.1 = 1.1)
错误衡量的选择
常见的二元分类的错误有弃真(把把对的拒之门外)与取伪(把敌人当做亲人)。他们在不同的场合有不同的权重,比如对于保密局的门禁系统来说取伪的错误权重是很高的。我们可以说放进来一个坏人比将一个自己人拒之门外的情形坏1000倍!那为什么是1000倍?
事实上1000并不是一个最佳的定量的做法,有时候只是我们直觉性的估计。在实务上我们的错误衡量有以下的两种:
1.有严格的逻辑推理与严格的说明(这种方法很困难)。
2.没有太多的理论保证,但是我们可以在电脑上相对容易的实现。
至于不同的问题我们会有不同的选择。
错误权重的等价
在实务上我们要在不同的错误上给予不同的权重,假如说我们要在一个二分的例子中给予一个点犯错误后的权重是其它点的1000倍,那么我们可以将情景等价于将这个点的错误权重变为1而在数量上*1000。这样我们就完成了从1000*1==1*1000的转化。在转化过后的问题上我们可以使用最基础的理论解决这个机器学习算法的问题。
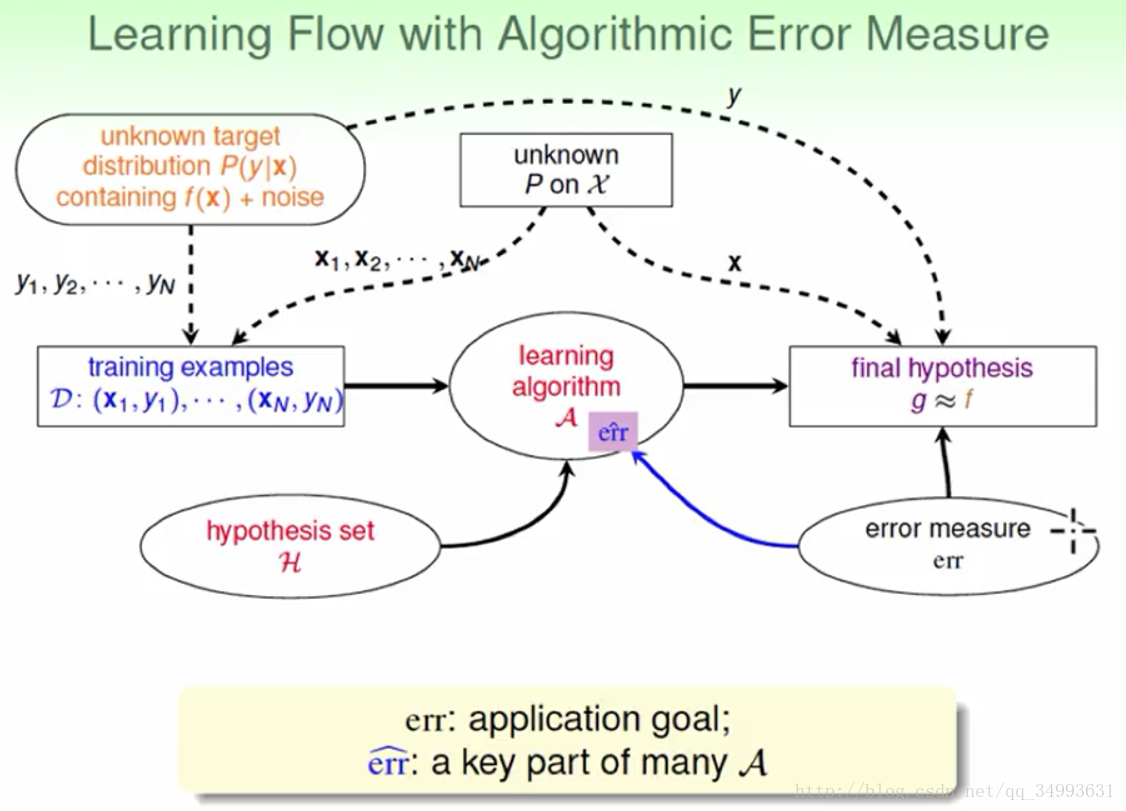
加上错误衡量之后的流程图
总结一下:我们的错误衡量引导了算法使得我们选到的最佳模型更加适合于我们的问题。
线性回归
引子
在一个二元分类的问题中我们通常得到的结果是1/0,而在分类的过程中我们会先计算一个得分函数然后在减去一个门槛值后判断它的正负,若为正则结果为1若为负结果为0。
事实上从某种角度来看,线性回归只是二元分类步骤中的一个截取,它没有后面取正负号的操作,它的输出结果为一个实数,而非0/1。我们称这样的数学模型为线性回归。
在传统上统计学家给出的结果是如下:
它的物理意义就是要提取多笔资料的特征用一个线性的函数所表示,我们要做的就是让我们资料的表现与我们函数之间的差距之和越小越好。进一步来说我们就是要找一个h(x)通过调整它的权重W来达到上述目的。(当然此时的W的维度包括常数在内)
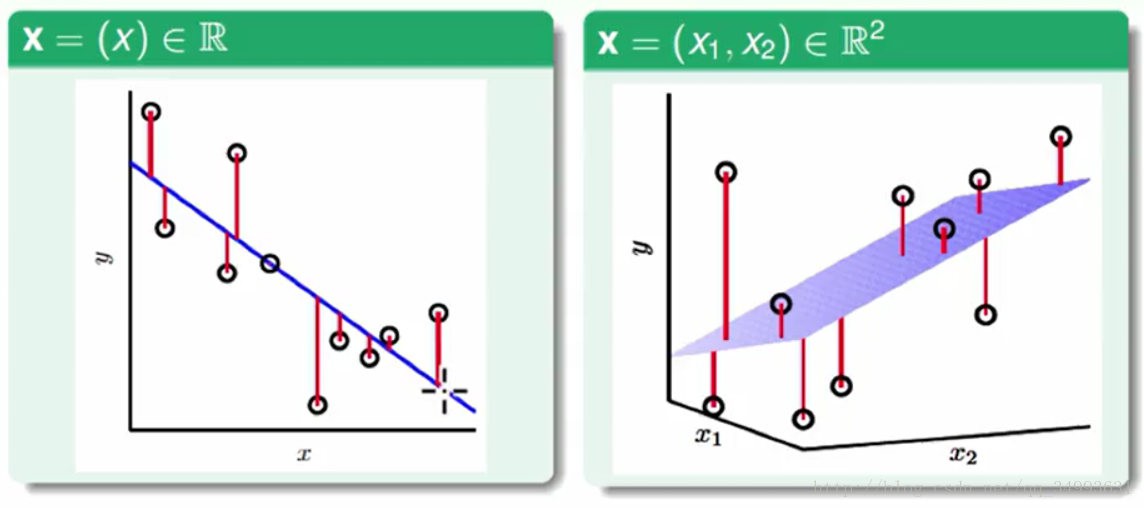
几何意义
图中的点代表我们资料的表现,而那条蓝色的线就是我们的h(x),每个点到线(或者超平面)的距离就是资料与我们线性模型的误差。我们的目的就是使得所有点到线的距离之和最小。
传统上我们的线性回归的误差计算为平方误差表现为下图:
进一步来说我们模型所犯的错误如下图所示:
左图中是模型h(x)在样本上犯的错误,右边是模型h(x)在总体数据上犯的错误,我们相信在VC维度的保障下我们可以从大量的数据中学到东西。也就是我们在大量数据下学习使得我们的模型的Ein很小就是我们下一步要完成的目标。
如何最小化Ein
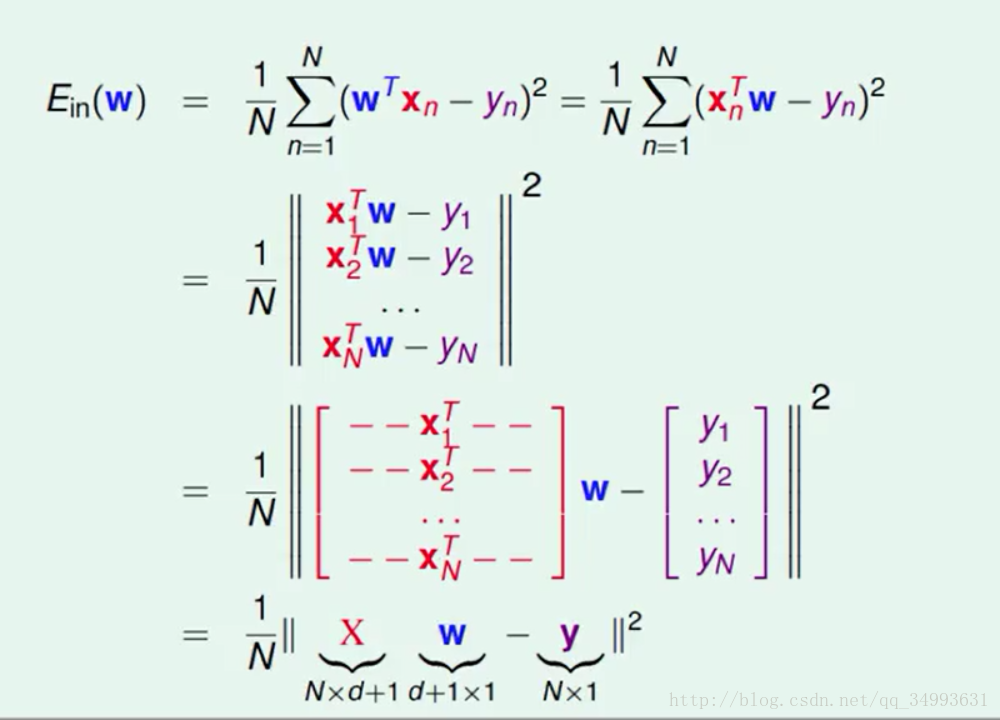
Ein的矩阵表示
由于一个h(x)对应的一个W向量而其他的x与y都为已知量所以我们对h(x)的优化也就是我们对W的优化所以下面的推到中只有W为变量:
经过一系列的推导我们将Ein写成了更为直观的矩阵的形式,我们要求的就是Ein最小时W的值是多少。经过一些数学上的推导我们发现Ein对应的函数是一个凸函数(大陆好像一般都是凹函数)如下图所示:
根据凸函数的性质我们可以知道在函数的梯度为0的时候我们可以得到函数的最小值,也就是我们要求的W正是Ein的梯度为0的时候所对应的W。
Ein梯度的表示与W的计算
上图从一维的w(单一变数)推广到了多维的W(向量)最后得到了最终的梯度表达式如上图下方所示。
令梯度为0我们可以得到W:
在上图的上方我们得到了最优的W的表达式,在大多数的情况下X的转置与X的乘积是有反矩阵的此时的W可以一步计算出来(它只有一个解)如上图左方所示,在不是反矩阵的情况下我们也会求出一个假的反矩阵来这个假的反矩阵与反矩阵有类似的性质(这种情况下会有多组解我们会选择其中的一组解)如上图右方所示。在实务上很多的软件都写好了求(假的)反矩阵的包我们可以直接调用。
这样我们就求出了最优的W,同时也求出了最优的h(x)。
线性回归的算法看起来像是一步登天没有经过看起来一步一步的学习,但是在整个过程中在最后Eout≈0我们说这个算法确实发生了学习只是学习的步骤隐藏起来了(如果我们编写一个程序就有直观的感受我们会有一次一次的迭代)。
Ein的另一种表现形式
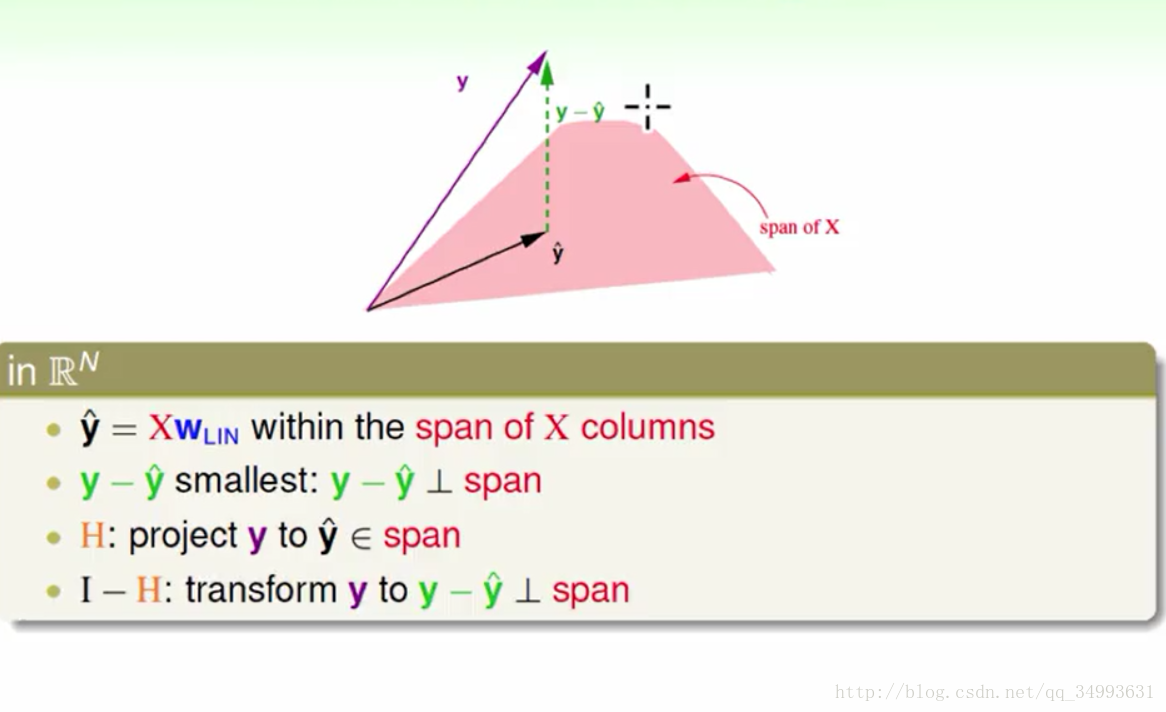
H矩阵的意义
如上图所示Ein可以用一个含有杂讯的式子来表示,在上图的式子中我们将y矩阵与他的线性变换分离开来我们得到了H矩阵。现在已知Hy = y hat(y上面加^),从线性代数的基础知识中我们知道H是一个y的线性变换如下图所示:
在图中粉红色部分为X矩阵展开的线性空间而y hat = XWlin所以y hat也在X矩阵所展开的线性空间上,而已知y在X的线性空间外则y - y hat 的向量的大小就是y与X空间上最近的距离(因为我们的y hat是一个最优解)。又知道y与y在X空间投影的距离最小,那么我们就知道y hat就是y在X空间上的投影。也就是我们的H矩阵是y到X空间的投影动作。同时也知道了(I - H)是y在X空间上取余数的动作(由y得到y-yhat的线性变换)。
如果我们用力计算的话我们会得到trace(I - H) = N - (d + 1),其中trace是矩阵对角线只和。它的物理意义是什么N个自由度的向量(x向量的个数与y向量维度都是N)投影到一个d+1维的空间里(x向量的维度)再经过取余数之后会得到余数的自由度为
N-(d+1),也就是y - y hat的维度。
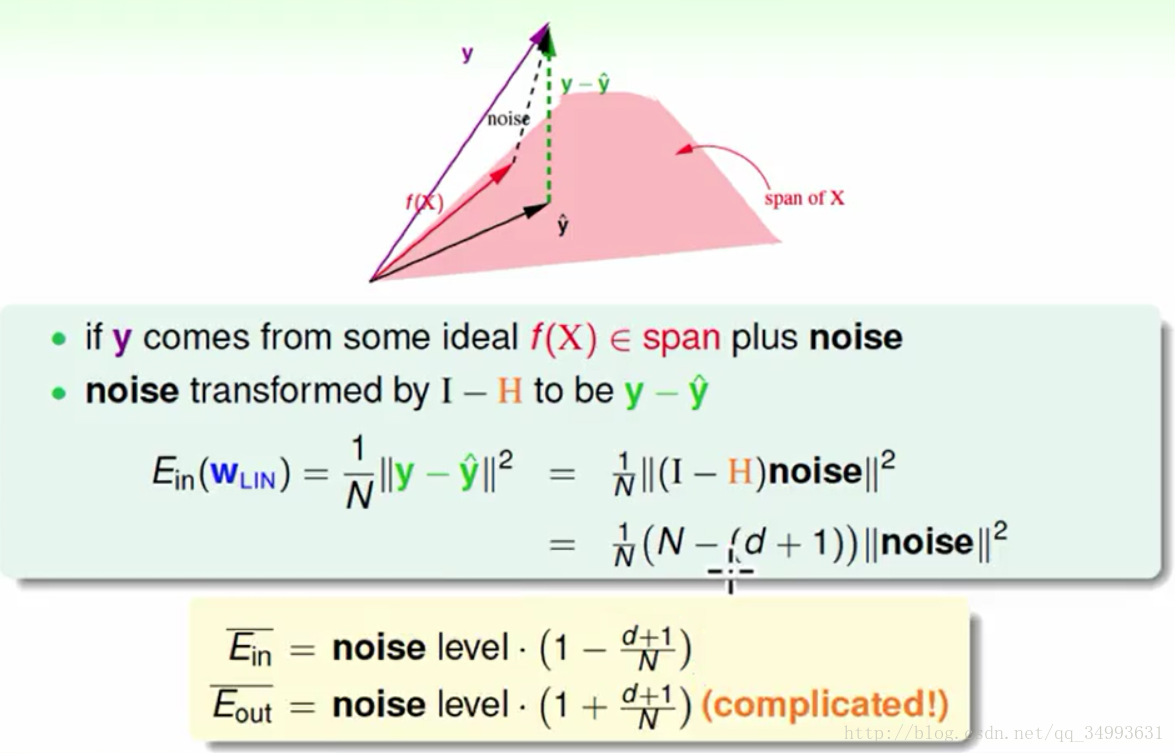
Ein的另一种表现形式
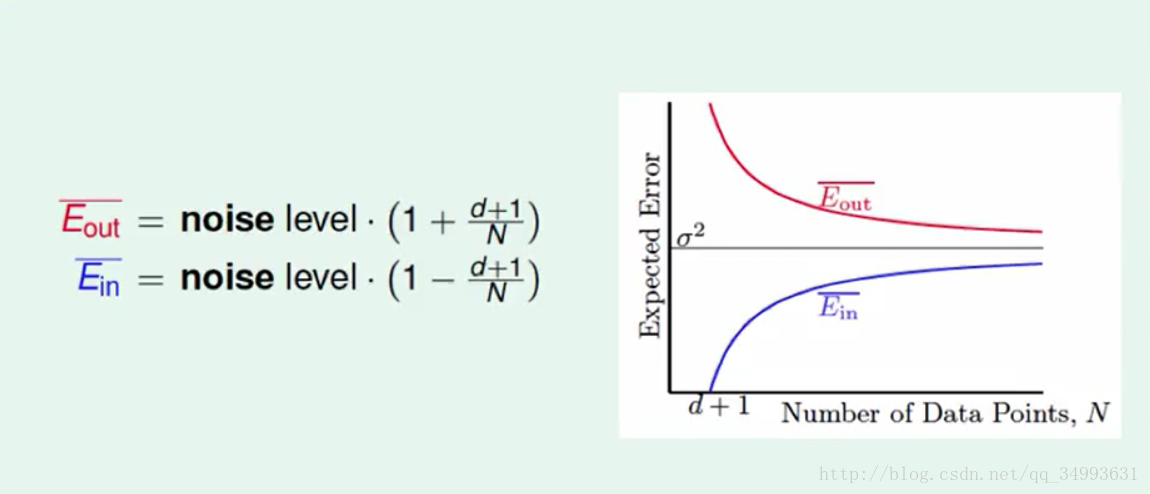
在上图上线性代数告诉我们我们的目标函数也在X空间中,而我们的标签y正是f(x)+noise的结果,而在加上我们讨论过的线性变换我们就会得出y - y hat = (I - H)noise,加上我们的trace(I - H) = N - (d + 1),在加上我们对noise做平均得到noise level,最后将这些结论带入以前的Ein表达式得到一个全新的Ein表达式如上图下方所示。与此同时Eout也可以采用类似的算法来计算只是相对困难如上图下方所示。
学习曲线
在经过上述的推导之后我们得到了如下曲线:
他描述了我们的资料量与我们平均可以的得到平均的Ein与Eout的关系,我们可以看出随着资料量的增大Ein的平均与Eout的平均越来越接近,而且如果在杂讯很小的情况下我们就能办到Eout≈0,此时我们学到了东西。

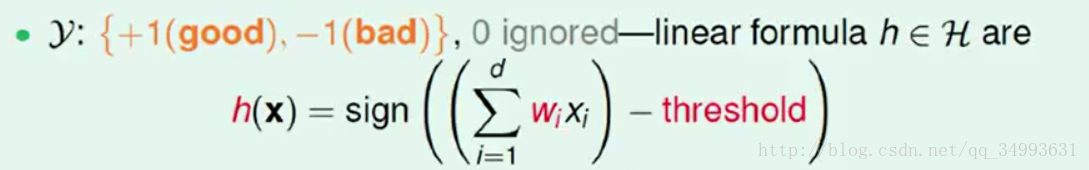











 浙公网安备 33010602011771号
浙公网安备 33010602011771号