作为经典的知识追踪方法,BKT(Bayes Knowledge Tracing)是最早提出以序列方式对学习者知识状态建模的方法。
本文旨在从HMM(Hidden Markov Model)角度推导现有论文中常见的一种BKT公式,如下图所示。
\[\begin{aligned}
p(L_t|1)&= \frac{(1 - p(S)) \cdot p(L_t)}{(1 - p(S)) \cdot p(L_t) + p(G) \cdot (1 - p(L_t))} \quad (1) \\
p(L_t|0)&=\frac{p(S) \cdot p(L_t)}{p(S) \cdot p(L_t) + (1 - p(G)) \cdot (1 - p(L_t))} \quad (2)\\
p(L_{t+1}) &= p(L_t|o_t)+p(T) \cdot (1 - p(L_t|o_t)) \quad (3)
\end{aligned}
\]
HMM
HMM 是关于时序的概率模型。HMM中存在观测变量,状态变量(不可观测)。
我们使用\(\left\{o_1, o_2, \cdots, o_t, \cdots \right\}\) 表示观测变量组成的序列,\(\left\{z_1, z_2, \cdots, z_t, \cdots \right\}\) 表示状态变量组成的序列, 其中t表示时间次序。
一般情况观测变量,状态变量取值范围为有限个离散值。为方便描述HMM与BKT的关系,本文假设观测变量,状态变量均只能取两个值,即\(\{0, 1\}\)。
HMM模型可使用三组参数描述,分别是初始状态变量分布\(\pi\),状态转移矩阵\(A\) 和发射矩阵\(B\)。
\(\pi\) 描述了状态变量初始值的分布,如下式所示。\(p(L_0)\) 为取值为0的概率,\(1 - p(L_0)\)为取值为1的概率。
\[\pi = \left[\begin{array}{c}
p(L_0) \\
1 - p(L_0)\\
\end{array}\right]
\]
状态转移矩阵\(A\)描述了状态变量由\(t-1\)时刻与\(t\)时刻的变换关系。我们这里使用BKT状态变量转移矩阵为例。known表示掌握知识状态,unknown表示未掌握状态。矩阵第二列表示,从t-1时刻unknown状态到t时刻known, unknown的状态概率分别为\(p(T)\), \(1-p(T)\)。第一列与第二列类似。
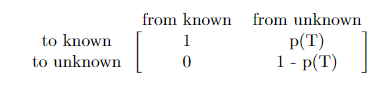
发射矩阵\(B\)描述了状态变量到观测变量的变换关系。类似地,我们以BKT中的发射矩阵为例,如下所示。该矩阵与状态转移矩阵解释类似,此处不再详细介绍。

基于\(A\), \(B\), \(\pi\) 我们可使用如下公式描述状态变量,观测变量的关系。
\[t = 1,
\begin{aligned}
p(z_{1}) &= \pi\\
p(o_{1}) &= B \cdot p(z_{1})
\end{aligned};
\forall t > 1,
\begin{aligned}
p(z_{t}) &= A \cdot p(z_{t-1})\\
p(o_{t}) &= B \cdot p(z_{t})
\end{aligned}
\]
BKT 概率公式推导
\(p(T)\), \(p(S)\), \(p(G)\) 为BKT模型的待学习参数。\(p(T)\) 表示学生从未掌握到掌握知识点的概率。\(p(S)\) 表示学生掌握知识点但是答错题目的概率。\(p(G)\) 表示学生未掌握知识点但是答对题目的概率。另外, \(p(L_{t})\) 表示学生在t时刻对知识点的掌握状态。\(A, B\)定义如下。
\[\begin{aligned}
A &= \left[\begin{array}{cc}
1 &p(T)\\
0 &1 - p(T)\\
\end{array}\right]\\
B &= \left[\begin{array}{cc}
1 - p(S) &p(G)\\
p(S) &1 - p(G)\\
\end{array}\right]
\end{aligned}
\]
t时刻,学生对知识点的掌握情况为
\(
p(z_{t}) = \left[\begin{array}{c}
p(L_{t}) \\
1 - p(L_{t})\\
\end{array}\right]\)
由发射矩阵 得:
\[\begin{aligned}
p(o_{t})
&= B\cdot p(z_{t})\\
&= \left[\begin{array}{cc}
1 - p(S) &p(G)\\
p(S) &1 - p(G)\\
\end{array}\right] \cdot \left[\begin{array}{c}
p(L_{t}) \\
1 - p(L_{t})\\
\end{array}\right] \\
&= \left[\begin{array}{c}
(1 - p(S)) \cdot p(L_t) + p(G) \cdot (1 - p(L_t))\\
p(S) \cdot p(L_t) + (1 - p(G)) \cdot (1 - p(L_t)) \\
\end{array}\right]\\
\end{aligned}
\]
由发射矩阵定义可知,
\[\begin{aligned}
p(z_t=1, o_t=1) &= (1 - p(S)) \cdot p(L_t)\\
p(o_t=1) &= (1 - p(S)) \cdot p(L_t) + p(G) \cdot (1 - p(L_t))\\
p(z_t=1|o_t=1) &=\frac{p(z_t=1, o_t=1)}{p(o_t=1)}\\
&= \frac{(1 - p(S)) \cdot p(L_t)}{(1 - p(S)) \cdot p(L_t) + p(G) \cdot (1 - p(L_t))}
\end{aligned}
\]
\(p(z_t=1| o_t=1)\) 为学生在t时刻答对题目,学会该知识的概率,即\(p(L_{t}|1)\),公式(1)推导完毕。
类似的我们也可以推导得到公式(2)。
对于公式(3),主要基于状态转移矩阵\(A\).
\[\begin{aligned}
p(z_{t+1}) &= A \cdot p(z_{t})\\
&= \left[\begin{array}{cc}
1 &p(T)\\
0 &1 - p(T)\\
\end{array}\right] \cdot \left[\begin{array}{c}
p(L_{t}) \\
1 - p(L_{t})\\
\end{array}\right] \\
&= \left[\begin{array}{cc}
p(L_t)+p(T) \cdot (1 - p(L_t))\\
(1 - p(T)) \cdot (1 - p(L_t))\\
\end{array}\right]
\end{aligned}
\]
由前述定义可知,
\[p(z_{t+1}) = \left[\begin{array}{c}
p(L_{t+1}) \\
1 - p(L_{t+1})\\
\end{array}\right]
\]
所以
\[p(L_{t+1}) = p(L_t)+p(T) \cdot (1 - p(L_t))
\]
\(p(L_t)\)由观测变量\(o_{t}\)决定其计算方式为公式(1)或(2)。我们使用\(p(L_{t}|o_{t})\)表示其计算结果。带入上式可得。至此,公式(3)推导完毕。
\[p(L_{t+1}) = p(L_t|o_t)+p(T) \cdot (1 - p(L_t|o_t))
\]
实现
https://github.com/lif323/BKT
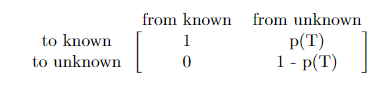



 浙公网安备 33010602011771号
浙公网安备 33010602011771号