卷积和卷积层

---

📝 卷积（Convolution）知识点总结

一、 数学定义（基础概念）

概念	描述
定义	卷积是一种数学运算，通过两个函数（或序列）生成第三个函数（或序列）。它衡量了一个函数对另一个函数的累积影响。
连续卷积
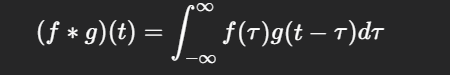离散卷积
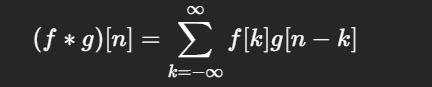核心操作

---

二、 卷积神经网络 (CNN) 中的卷积层

在 CNN 中，卷积操作是一种特征提取机制，实际操作中通常使用交叉相关来代替严格的数学卷积。

1. 核心组件与参数

组件/参数	类型	作用
卷积核 (Kernel/Filter)	可学习参数	一个小的权重矩阵，用于检测输入数据中的特定局部特征（如边缘、纹理）。
偏移 (Bias)	可学习参数	加在乘加结果上的常数项，增强模型表达能力。
输入 (Input)	数据	原始图像或前一层的特征图。
输出 (Output)	特征图 (Feature Map)	记录了输入数据中对应特征的位置和激活强度。

2. 卷积运算的优势

1. 参数共享 (Parameter Sharing)： 同一个卷积核在整个输入上滑动并重复使用，极大减少了需要学习的参数数量。
2. 局部感知 (Local Receptive Field)： 每个输出神经元只与输入的一个局部区域连接，模拟生物视觉系统，高效提取空间局部特征。
3. 平移不变性： 结合池化层，使模型对输入数据的微小平移具有鲁棒性。

---

三、 卷积层的超参数 (Hyperparameters)

这些参数在训练前设定，控制卷积操作的行为和输出形状。

超参数	描述	作用
核矩阵大小 (K)	卷积核的尺寸（如 3*3）。	决定了局部感受野的大小。
步幅 (Stride, S)	卷积核每次滑动的像素距离。	降采样：$S>1$ 时大幅减小输出尺寸，提高计算效率。
填充 (Padding, P)	在输入周围添加的额外像素（通常为0）。	保护边缘信息；控制输出尺寸不减少（例如 "Same" Padding）。

---

四、 卷积层之后的信息流失与处理

阶段	信息发生变化	目的
激活函数 (e.g., ReLU)	非线性过滤：将负激活值置零。	引入非线性能力，使网络能学习更复杂的映射。
池化层 (Pooling)	有损压缩/降维：通常只保留局部区域的最大值（Max Pooling）。	增强鲁棒性和平移不变性；大幅减少后续计算量。

---