ReLU函数及它的导数

ReLU 函数

ReLU（Rectified Linear Unit，修正线性单元）是目前在深度学习中最常用的激活函数。它的数学表达式非常简单：

f(x) = max(0, x)

这意味着当输入 $x$ 大于 0 时，输出就是 $x$ 本身；当输入 $x$ 小于或等于 0 时，输出就是 0。

ReLU 的特点

---

• 计算高效：相比于 sigmoid 和 tanh，ReLU 只需要一个简单的阈值判断，不需要复杂的指数运算，这使得计算速度非常快。
• 解决了梯度消失问题：当输入 $x > 0$ 时，ReLU 的导数恒为 1。这保证了在正向传播过程中，梯度不会像 sigmoid 或 tanh 那样随着层数增加而变得越来越小，从而有效缓解了梯度消失问题，加快了模型的收敛速度。
• 稀疏性：当输入 $x \le 0$ 时，ReLU 的输出为 0。这使得一部分神经元输出为 0，从而形成了网络的稀疏表示。这种稀疏性有助于提高模型的泛化能力。

缺点

---

• 死亡 ReLU 问题（Dying ReLU）：当一个神经元的输入始终为负时，它的输出将永远是 0。在这种情况下，这个神经元的梯度也永远是 0，导致它在反向传播过程中无法更新权重，就像“死亡”了一样。

ReLU 函数的导数

ReLU 的导数也同样简单：

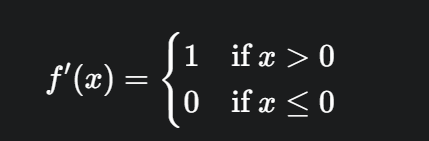
这里需要注意，当 $x = 0$ 时，ReLU 函数是不可导的。但在实际应用中，我们通常将 $x=0$ 处的导数视为 0 或 1。通常的做法是将其设置为 0，因为在反向传播中，当 $x \le 0$ 时，梯度为 0，不会更新权重，这与“死亡 ReLU”的特性相符。

在代码中如何实现

---

在 NumPy 中，你可以这样实现 ReLU 及其导数：

import numpy as np

class ReLU:
    def forward(self, x):
        self.x = x
        return np.maximum(0, x)
        
    def backward(self, G):
        grad = G.copy()
        grad[self.x <= 0] = 0
        return grad

在这个实现中，forward 方法保存了输入 self.x，backward 方法则利用这个输入来判断哪些位置的梯度应该为 0，从而实现 ReLU 的反向传播。