【稀疏矩阵】

 

 

/*
稀疏矩阵 
说明:
如果在矩阵中，多数的元素并没有资料，称此矩阵为稀疏矩阵（sparse matrix ）， 由于矩阵在程式中常使用二维阵列表示，二维
阵列的大小与使用的记忆体空间成正比，如果多数的元素没有资料 ， 则会造成记忆体空间的浪费 ， 为 此 ， 必须设计稀疏矩阵
的阵列储存方式 ， 利用较少的记忆体空间储存完整的矩阵资讯。
解法:
在这边所介绍的方法较为简单，阵列只储存矩阵的行数、列数与有资料的索引位置及其值，在需要使用矩阵资料时，再透过程式运算
加以还原，例如若矩阵资料如下 ，其中0表示矩阵中该位置没有资料：
0 0 0 0 0 0
0 3 0 0 0 0
0 0 0 6 0 0
0 0 9 0 0 0
0 0 0 0 12 0
这个矩阵是5X6矩阵，非零元素有4个，您要使用的阵列第一列记录其列数、行数与非零元素个数：
5 6 4
阵列的第二列起，记录其位置的列索引、行索引与储存值：
1 1 3
2 3 6
3 2 9
4 4 12
所以原本要用30个元素储存的矩阵资讯，现在只使用了15个元素来储存，节省了不少记忆体的使用。
*/

#include<stdio.h>
#include<stdlib.h>

int main(void){
    int num[5][3] = {{5,6,4}, {1,1,3},{2,3,6},{3,2,9},{4,4,12}};
    int i, j, k = 1;
    printf("sparse matrix: \n");
    for(i = 0; i < 5; i++){
        for(j = 0; j < 3; j++){
            printf("%4d ", num[i][j]);
        }
        putchar('\n');
    }
    
    printf("\nmatrix还原：\n");
    for(i = 0; i < num[0][0]; i++){
        for(j = 0; j < num[0][1]; j++){
            if(k < num[0][2] && i == num[k][0] && j == num[k][1]){
                printf("%4d ", num[k][2]);
                k++;
            }else{
                printf("%4d", 0);
            }
        }
        putchar('\n');
    }
    
    return 0;
} 

这个代码貌似有点问题，运行结果就不贴了。

 

这是我写的代码：

/*
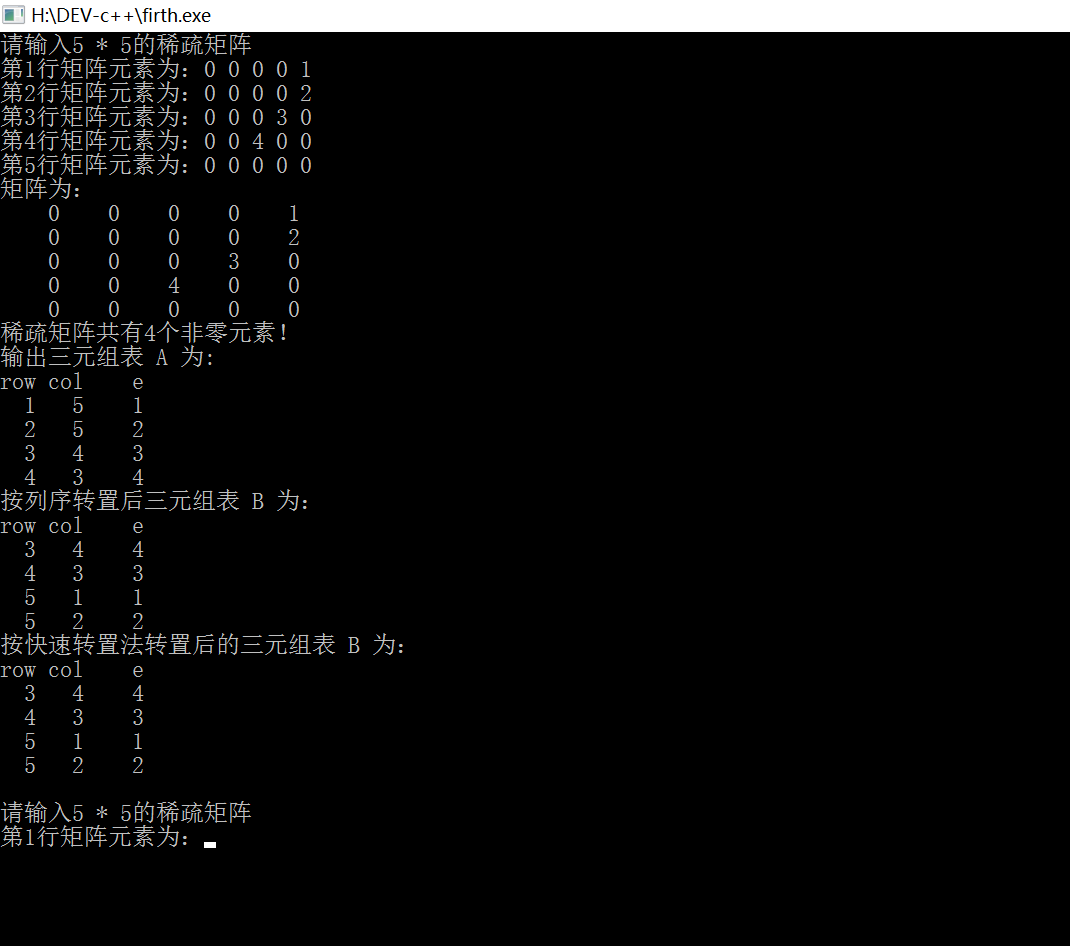
稀疏矩阵的简单运算：
 
列序递增转置
一次定位快速转置

201701031018
*/

#include <stdio.h>
#include <string.h>


#define R 5
#define C 5
#define MAX 1000
#define MAXS 10 

typedef struct
{
    int row, col;        //非零元素的行数，列数，值
    int e;
}Triple;

typedef struct
{
    Triple data[MAX+1];
    int m, n, len;        //稀疏矩阵的行数，列数，非零元素个数
}TSMatrix;

//函数声明 
void print(TSMatrix A);        //输出三元组表    
TSMatrix create(TSMatrix A, int a[R][C], TSMatrix B);        //创建稀疏矩阵 
void TranposeTSMatrix(TSMatrix A, TSMatrix *B);                //列序递增转置 
void FastTranposeTSMatrix(TSMatrix A, TSMatrix *B);         //一次定位快速转置 

//输出三元组表
void print(TSMatrix A)
{
    int i;
    
    printf("row col    e\n");
    for(i = 1; i <= A.len; i++)
    {
        printf("%3d%4d%5d\n", A.data[i].row, A.data[i].col, A.data[i].e);
    }
}

//创建稀疏矩阵
TSMatrix create(TSMatrix A, int a[R][C], TSMatrix B)
{
    int i, j;
    A.m = R;
    A.n = C;
    A.len = 0;
     
    printf("请输入%d * %d的稀疏矩阵\n", A.m, A.n);
    for(i = 0, j = 0; i < A.m; i++, j = 0)
    {
        printf("第%d行矩阵元素为：", i+1);
        scanf("%d%d%d%d%d", &a[i][j], &a[i][j+1], &a[i][j+2], &a[i][j+3], &a[i][j+4]);
//        printf("\n");
    }    //输入稀疏矩阵
    
    printf("矩阵为：\n");
    for(i=0; i<A.m;i++)
    {
        for(j=0; j<A.n;j++)
        { 
            if(a[i][j] != 0)
            {
                A.len++;
                A.data[A.len].row = i+1;
                A.data[A.len].col = j+1;
                A.data[A.len].e = a[i][j]; 
            }
            printf("%5d", a[i][j]);
        }
        printf("\n");
    }    //输出矩阵，并统计非零元素个数A.len 
    
    if(A.len < 7)
    {
        printf("稀疏矩阵共有%d个非零元素！\n", A.len);
        //输出三元组表A 
        printf("输出三元组表 A 为:\n");
        print(A);
        
        //输出 按列序转置后 的三元组表B 
        printf("按列序转置后三元组表 B 为：\n"); 
        TranposeTSMatrix(A, &B);
        print(B);
        
        //输出 快速转置法  的三元组表B 
        printf("按快速转置法转置后的三元组表 B 为：\n");
        FastTranposeTSMatrix(A, &B);
        print(B);
    }
    else
    {
        printf("因为 A.len = %d, A.len >= %f ", A.len, (5*5*0.3));
        printf("所以 你输入的不是稀疏矩阵! \n");
//        create(A, a, B);
    }    //判断是否为稀疏矩阵，若不是则重新输入 
    
    printf("\n");
    return A;
}

//列序递增转置 
void TranposeTSMatrix(TSMatrix A, TSMatrix *B){
    int i, j, k;
    B->m = A.m;
    B->n = A.n;
    B->len = A.len;
    
    if(B->len > 0)
    {
        j = 1; 
        for(k = 1; k <= B->n; k++)
        {
            for(i = 1; i <= B->len; i++)
            {
                if(A.data[i].col == k)
                {
                    B->data[j].row = A.data[i].col;
                    B->data[j].col = A.data[i].row;
                    B->data[j].e = A.data[i].e; 
                    j++;
                }
            }
        }
    }
}    //按列序递增转置 

//一次定位快速转置 
void FastTranposeTSMatrix(TSMatrix A, TSMatrix *B){
    int col, t, p, q;
    int num[MAXS],  position[MAXS];
    B->len = A.len;
    B->m = A.m;
    B->n = A.n;
    
    if(B->len)
    {
        for(col = 1; col <= A.n; col++)
            num[col] = 0;
        for(t = 1; t <= A.len; t++)
            num[A.data[t].col]++;
        position[1] = 1;
        for(col = 2; col <= A.n; col++)
            position[col] = position[col-1] + num[col-1];
        for(p = 1; p <= A.len; p++)
        {
            col = A.data[p].col;
            q = position[col];
            B->data[q].row = A.data[p].col;
            B->data[q].col = A.data[p].row;
            B->data[q].e = A.data[p].e;
            position[col]++; 
        }
    }
}    //快速转置法 


int main(void)
{
    TSMatrix A;
    TSMatrix B;
    int a[R][C], i = 1;
    
    while(i){
        create(A, a, B);
    }
    
    return 0;
}

 

运行结果：