AcWing 97. 约数之和

https://www.acwing.com/problem/content/description/99/

 

 

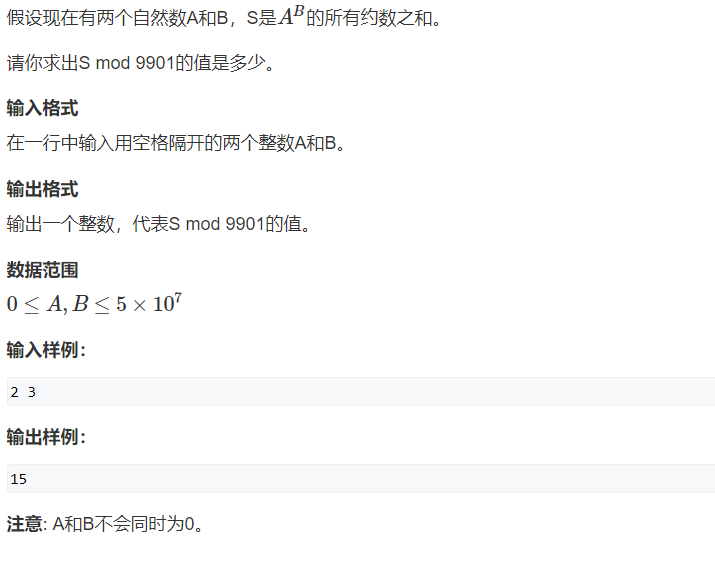
 求约数和的办法：

唯一分解定理：可以将一个数分解成若干素数的乘积，且分解方案唯一，n=p1^m1*p2^m2*...pk^mk.

任何一个约数可以表示为p1^x1*p2^x2*...pk^xk.(0<=x<=m).

所以总的约数和为(p1^0+p1^1+...+p1^m1)*(p2^0+p2^1+...+p2^m2)*...*(pk^0+pk^1+...+pk^mk).

由于b的范围是小于等于5e7，所以直接这样做会超时。

不过由于最后结果要模mod(mod=9901)，可以发现p^x%mod具有周期性，且周期不会超过mod，因为p%mod确定后，((p%mod)*p)%mod就确定，且取模后的值不会超过mod个.

所以可以求出周期，再求出一个周期里的数的总和，再求出完整周期外的数的总和。

代码：

  1 #include <bits/stdc++.h>
  2 typedef long long ll;
  3 using namespace std;
  4 
  5 const int N=1e4+5;
  6 const int mod=9901;
  7 
  8 int p[N],num[N];
  9 int cnt=0;
 10 int pos[9905];
 11 
 12 ll pw(ll x,ll y,int MOD) {
 13     x%=MOD;
 14     ll res=1;
 15     while(y) {
 16         if(y&1) res=res*x%MOD;
 17         x=x*x%MOD;
 18         y>>=1;
 19     }
 20     return res;
 21 }
 22 
 23 ll inv(ll a,ll p) {//乘法逆元
 24     return pw(a,p-2,p);
 25 }
 26 
 27 void Divide(int x) {//素因数分解
 28     cnt=0;
 29     for(int i=2;i<=sqrt(x);i++) {
 30         if(x%i==0) {
 31             p[++cnt]=i;
 32             while(x%i==0) {
 33                 num[cnt]++;
 34                 x/=i;
 35             }
 36         }
 37     }
 38     if(x>1) {
 39         p[++cnt]=x;num[cnt]=1;
 40     }
 41 }
 42 
 43 int main() {
 44     ll a,b;
 45     scanf("%lld%lld",&a,&b);
 46     if(a==0) {
 47         printf("0\n");return 0;
 48     }
 49     Divide(a);
 50     ll ans=1;
 51     for(int i=1;i<=cnt;i++) {
 52         ll plus=0;
 53         for(int j=0;j<mod;j++) pos[j]=0;
 54         bool flg=false;
 55         ll s,l,r,base=1;
 56         pos[1]=1;
 57         for(int j=1;j<=b*num[i];j++) {//在总长度范围内找周期并求出周期长度，完整周期起始点
 58             base=base*p[i]%mod;
 59             if(pos[base]) {
 60                 flg=true;
 61                 l=pos[base];r=j+1;s=base;
 62                 break;
 63             }
 64             else pos[base]=j+1;
 65         }
 66         if(flg) {//若找到周期
 67             ll t=s;
 68             for(int j=l+1;j<r;j++) {//求出一个周期的数的总和
 69                 s=s*p[i]%mod;
 70                 t=(t+s)%mod;
 71             }
 72             plus=(plus+t*(((b*num[i]%mod+1-(l-1))%mod+mod)*inv(r-l,mod)))%mod;//求全部完整周期的数的总和
 73             base=1;
 74             for(int j=1;j<l;j++) {//求完整周期前的数的总和
 75                 if(j==1) plus++;
 76                 else {
 77                     base=base*p[i]%mod;
 78                     plus=(plus+base)%mod;
 79                 }
 80             }
 81             ll tmp=b*num[i]+1-(b*num[i]+1-(l-1))%(r-l)+1;
 82             base=pw(p[i],tmp-1,mod);
 83             for(int j=tmp;j<=b*num[i]+1;j++) {//求完整周期后的数的总和
 84                 if(j==tmp) plus=(plus+base)%mod;
 85                 else {
 86                     base=base*p[i]%mod;
 87                     plus=(plus+base)%mod;
 88                 }
 89             }
 90         }else {//若没找到周期，朴素计算
 91             base=plus=1;
 92             for(int j=1;j<=b*num[i];j++) {
 93                 base=base*p[i]%mod;
 94                 plus=(plus+base)%mod;
 95             }
 96         }
 97         ans=ans*plus%mod;
 98     }
 99     printf("%lld\n",ans);
100     return 0;
101 }

 

posted @ 2020-07-03 01:41  俩小圈  阅读(171)  评论(0)    收藏  举报