ng-深度学习-课程笔记-8: 超参数调试，Batch正则(Week3)

1 调试处理( tuning process )

如下图所示，ng认为学习速率α是需要调试的最重要的超参数。

其次重要的是momentum算法的β参数（一般设为0.9），隐藏单元数和mini-batch的大小。

第三重要的是神经网络的层数和学习率衰减

adam算法的三个参数一般不调整，设定为0.9, 0.999, 10^-8。

注意这些直觉是ng的经验，ng自己说了，可能其它的深度学习研究者是不这么认为的。

那么如何选择参数呢？下面介绍两个策略，随机搜索和精细搜索。

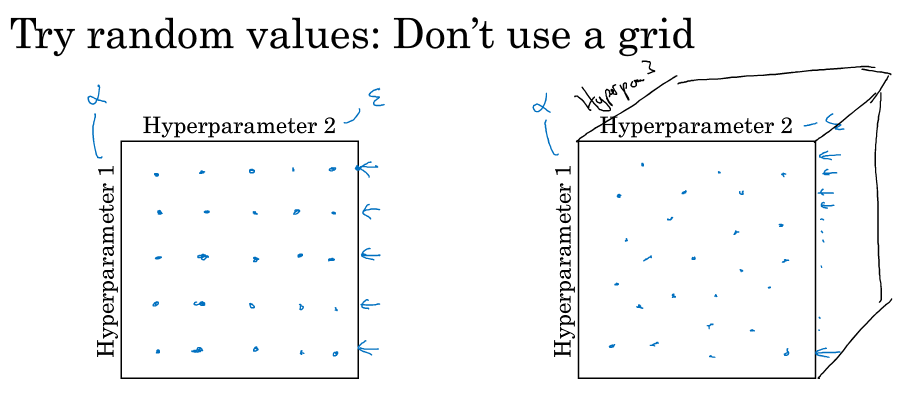
早一代的机器学习算法中，如下图左侧，会在网格中比如按5*5的行列取样点进行尝试，参数少的话这么做是可以的。

在深度学习中，我们做的是随机选择点，如下图右侧，在网格中随机选25个点进行尝试，因为对于你要解决的问题你很难知道哪个超参数最重要，比如参数1是α，参数2是ε，α是比较重要的需要调整，而ε一般不需要怎么调整，你就会发现不管ε怎么变都没多大影响，但是α只取了5个点进行尝试，如果你随机取的话，可能α就进行了更多点的尝试。

 

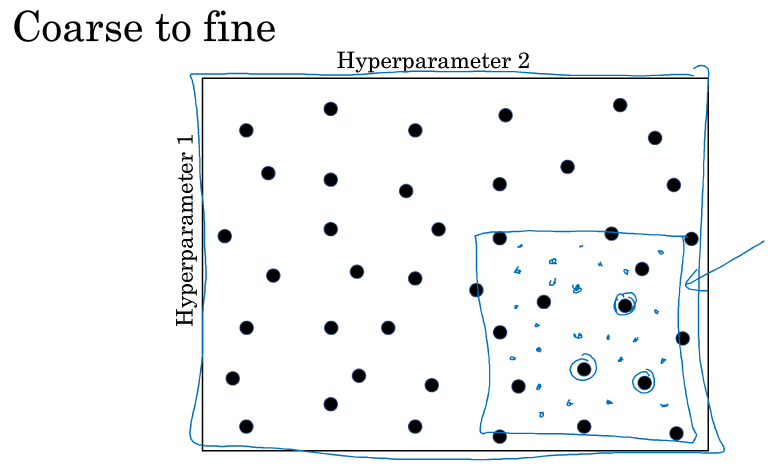
另一个惯用的策略是从粗糙到精细( coarse to fine )，当你用随机取点得到最好的点时，你可能会发现周围的点效果也很好，你就缩小范围，在这个更小的这个方格内做随机取点尝试，更密集地取值。

 

2 为超参数选择合适的范围( Using an appropriate scale to pick hyperparameters )

对于隐藏单元数比如说从50-100随机选一个数，或者对于隐藏层数从2-4随机选一个数，看上去还是挺合理的。

但是对于其它超参来说，比如学习率，如果你在0.0001和1之间随机取值，那么取到0.1到1之间的数的概率是90%，而在0.0001和0.1之间我们就很难取到数，这是不合理的，这个时候应该分段用log来取，0.0001到0.001之间用( -4到-3之间随机取），0.001到0.01之间用（-3到-2之间随机取），0.01到0.1之间用（-2到-1之间随机取），0.1到1之间用（-1到0随机取），可以认为是在-4到0之间随机取一个值。在python中可用 10 ^ ( -4 * np.random.rand() ) 表示在0.0001和1之间随机取一个值。

另外一个问题是给β取值，比如你认为0.9到0.999是搜索范围，那么0.9意味着平均10个值，0.999意味着平均1000个值，这种情况我们考虑1-β的范围为0.001到0.1，用上面所说的方法分成0.001到0.01之间用（-3到-2之间随机取），0.01到0.1之间用（-2到-1之间随机取），可以认为是在在-3到-1之间随机取一个值。因为在不同范围变化的造成的变化大小不同，所以需要这样来取值，举个例子，当β很靠近1时候，小小的变化会造成很大的变化，比如0.9990到0.9995，一个是平均1000个值，一个是平均2000个值。而从0.9变化到0.9005，都是平均10个值，造成的变化很小。在靠近1的区域，需要更密集地取值。

 

3 超参数训练的实践：Pandas VS Caviar ( Hyperparameters tuning in practice: Pandas vs Caviar )

Babysitting one model：在你CPU/GPU资源匮乏，计算能力不足的时候，训练一个模型，每天观察你模型的学习曲线，每天做一些参数的调整来使你模型保持良好的训练表现。

Training many models in parallel：同时训练不同参数的模型，观察它们的学习曲线（比如代价函数的下降曲线），选择最好的那一个。

ng把第一种方法称为pandas，因为熊猫有了孩子后，它们的孩子非常少，它们花很多经历抚养熊猫宝宝确保它能成活。

第二种方法称为caviar，它类似鱼类的行为，它会产生很多卵，但不对任何一个多加照料，只希望其中一个，其中一群能够表现出色。

 

4 网络的归一化( Normalizing activations in a network )

之前讲过对神经网络的原始特征输入进行归一化，可以加速训练，更快收敛。

同理，对于某一层的输出，我们也可以做归一化，这样利于下一层的参数训练，这就是Batch Normalization。

深度学习的文献中存在争议，有人觉得在每一层的激活之后再归一化，有人觉得再激活之前先归一化，ng的默认选择是后一种，对z进行归一化，然后再激活。

具体怎么做呢，如下图所示，对于每一层，求出给定样本的均值和方差，用原来的每个z减去均值，再除以标准差，为了防止分母为0给方差加上一个很小的ε，这样得到的就是一个均值为0，方差为1的一些数据。和原始特征输入不一样的是，我们不想让隐藏单元总是含有均值为0，方差为1的数据，也许隐藏单元含有不同的分布会更有意义，所以这里加多一步计算，乘以$\gamma$，然后加上$\beta$，这两个参数通过梯度下降学习得到，跟权重类似，它使得你可以构造含有其他均值和方差的隐藏单元数据，如果$\gamma$为标准差（加了ε的），$\beta$为均值，那么这个z就是原来的z，相当于没有变化。

对于后面那个公式，举个例子，比如我们想利用simoid的特性，不想让所有数据都集中在中间靠近0的那一块区域，我们想让它的方差更大，所以对它进行运算变化。或者可以理解成我们把隐藏层的均值和方差限定为某个值，不单单是0和1，而是这个值有更多选择，它由两个参数$\gamma$和$\beta$来学习，这里注意一下$\gamma$和$\beta$的维度和z是一致的，(n,1)，n表示该隐藏层的单元数。

5 Batch Norm为什么奏效( Why does Batch Norm work ? )

假如我在第3层得到了一些值，第3层到输出层之间的网络在做一个对（第三层的输入，最终输出）的映射预测，但是训练的时候前面的第2层第1层的权重也会改变，它会对第三层造成一定的影响。我们在第三层做了一个BN，就认为是把第三层的输入做了一个规范化，把数据规范在均值和方差为某个值的一个分布上。可以理解为这样做减少了前层对后层的影响，后层更容易去适应前层的更新，使每层可以自己学习，稍微独立于其它层，这有助于加速整个网络的学习。

BN还有一个轻微的正则化作用，首先对均值和方差的计算是在mini-batch上进行而不是整个数据集进行的，那本身就含有一定的噪音。其次在利用均值和方差进行转换的时候，因为均值和方差是带噪音的，所以这个过程也会加入噪音。所以它对隐藏单元施加了一些噪音，使得后层的隐藏单元不过分依赖任何一个隐藏单元。因为添加的噪音很微小，并不是很大的正则，可以把它和dropout一起用。顺带一说，BN不是正则，不要把它看成正则。

 

6 测试时的Batch Norm( Batch Norm at test time )

在训练的时候我们在一个mini-batch上做了BN，那测试的时候对于一个样本，如何来实施BN呢，估算u和方差的方式有好多种，ng介绍了一种做法。

对于某个隐藏单元，我们对每个mini-batch求出的u做指数加权平均得到一个u，对每个mini-batch求出的方差做指数加权平均得到一个方差，用得到的这两个数作为测试时那个隐藏单元进行运算的u和方差。

 

7 softmax回归( softmax regression )

这一节讲多分类和softmax。

约定符号C表示类别个数，则输出层的单元个数为C，输出C个概率，表示分到某一类的概率为多少，C个概率加起来为1，这一层就是平常说的softmax层。

softmax层是如何计算的呢，首先z跟往常的计算方法一样，然后计算t = e ^ z，如下图所示，假设有4个类别要分类，z的shape是4*1，t也是4*1。

然后计算a，a就是计算（某个分量t）占（4个t分量的和）的比例，这就是分到各个类别的概率。

softmax层的特殊之处就是它是输入一列向量，输出一列向量，它是整个层的一个激活函数。而之前的sigmoid或relu都是从实数到实数，是某个单元的激活。

softmax这个名字的来源是与hardmax进行对比，hardmax就是把向量中最大的那个置1，其它置0。

softmax是逻辑回归的推广，当softmax的C等于2的时候实际上就是一个逻辑回归。

 

然后我们来看看softmax的损失计算，和逻辑回归的损失有点类似，它计算每个输出单元和真实概率的交叉熵然后累加，这样，对于真实值为0的那样项就全部为0了，所以在优化的时候就是使得真实值为1的那个单元的输出概率尽量大，交叉熵就会尽量小。另外，如果想自己实现softmax的反向传播的话，记住最后一层的$dz = \hat{y} - y$，可以自己推导验证一下。

 

8 深度学习框架和Tensorflow( deep learning framework and tensorflow)

最后两节讲的是深度学习框架的选择和tensorflow的基本使用，这些我就不记录了。