第二次作业-多层感知机

 

 3.线性回归和softmax回归

线性回归

在机器学习领域中的大多数任务通常都与预测（prediction）有关。 当我们想预测一个数值时，就会涉及到回归问题。

线性回归（linear regression）在回归的各种标准工具中最简单而且最流行。它可以追溯到19世纪初。线性回归基于几个简单的假设：首先，假设自变量xx和因变量yy之间的关系是线性的，即y可以表示为x中元素的加权和，这里通常允许包含观测值的一些噪声；其次，我们假设任何噪声都比较正常，如噪声遵循正态分布。

为了解释线性回归，我们举一个实际的例子：我们希望根据房屋的面积（平方英尺）和房龄（年）来估算房屋价格（美元）。为了开发一个能预测房价的模型，我们需要收集一个真实的数据集。这个数据集包括了房屋的销售价格、面积和房龄。在机器学习的术语中，该数据集称为训练数据集（training data set）或训练集（training set），每行数据（在这个例子中是与一次房屋交易相对应的数据）称为样本（sample），也可以称为数据点（data point）或数据样本（data instance）。我们要试图预测的目标（在这个例子中是房屋价格）称为标签（label）或目标（target）。预测所依据的自变量（面积和房龄）称为特征（feature）或协变量（covariate）。

线性假设是指目标可以表示为特征的加权和。权重决定了每个特征对我们预测值的影响。偏置是指当所有特征都取值为0时，预测值应该为多少。即使现实中不会有任何房子的面积是0或房龄正好是0年，我们仍然需要偏置项。如果没有偏置项，我们模型的表达能力将受到限制。

损失函数

在我们开始考虑如何用模型拟合（fit）数据之前，我们需要确定一个拟合程度的度量。损失函数能够量化目标的实际值与预测值之间的差距。通常我们会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0。

通常用均方误差函数作为损失函数，系数1/2是为了之后方便对平方求导。

 

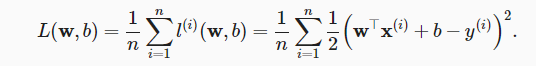
梯度下降

梯度下降最简单的用法是计算损失函数（数据集中所有样本的损失均值）关于模型参数的导数（在这里也可以称为梯度）。但实际中的执行可能会非常慢：因为在每一次更新参数之前，我们必须遍历整个数据集。因此，我们通常会在每次需要计算更新的时候随机抽取一小批样本，这种变体叫做小批量随机梯度下降（minibatch stochastic gradient descent）。

在每次迭代中，我们首先随机抽样一个小批量B，它是由固定数量的训练样本组成的。然后，我们计算小批量的平均损失关于模型参数的导数（也可以称为梯度）。最后，我们将梯度乘以一个预先确定的正数η，并从当前参数的值中减掉。

 

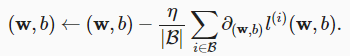
算法的步骤如下：（1）初始化模型参数的值，如随机初始化；（2）从数据集中随机抽取小批量样本且在负梯度的方向上更新参数，并不断迭代这一步骤。对于平方损失和仿射变换，我们可以明确地写成如下形式:

 

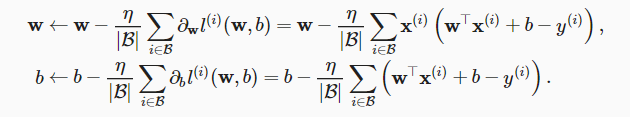
  上式中的w和x都是向量。在这里，更优雅的向量表示法比系数表示法（如w1,w2,…,wd）更具可读性。 |B|表示每个小批量中的样本数，这也称为批量大小（batch size）。η表示学习率（learning rate）。批量大小和学习率的值通常是手动预先指定，而不是通过模型训练得到的。这些可以调整但不在训练过程中更新的参数称为超参数（hyperparameter）。 调参（hyperparameter tuning）是选择超参数的过程。超参数通常是我们根据训练迭代结果来调整的，而训练迭代结果是在独立的验证数据集（validation dataset）上评估得到的。

 softmax回归

Softmax回归虽然名为回归，但是本质上是一个分类模型，模型的输出为对每一类别的概率预测，一般取其中最大值的那一类最为预测结果。

类似的还有logistic回归，logistic本质是一个二分类模型，属于softmax回归的特殊情况。

接下来从零开始实现softmax回归

对于交叉熵部分得数学推导有点没看懂。。。

 

 

 

 

 

 

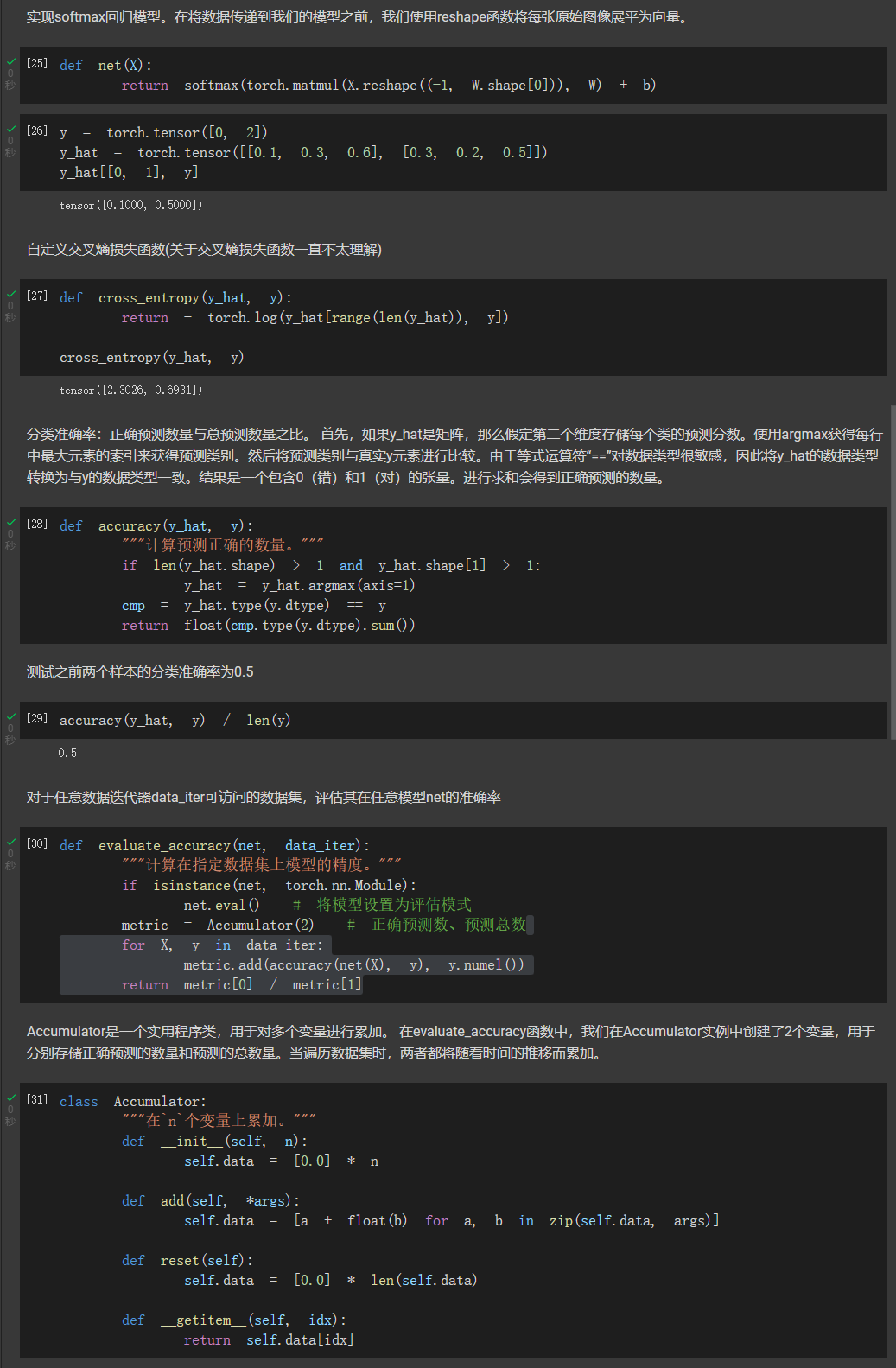
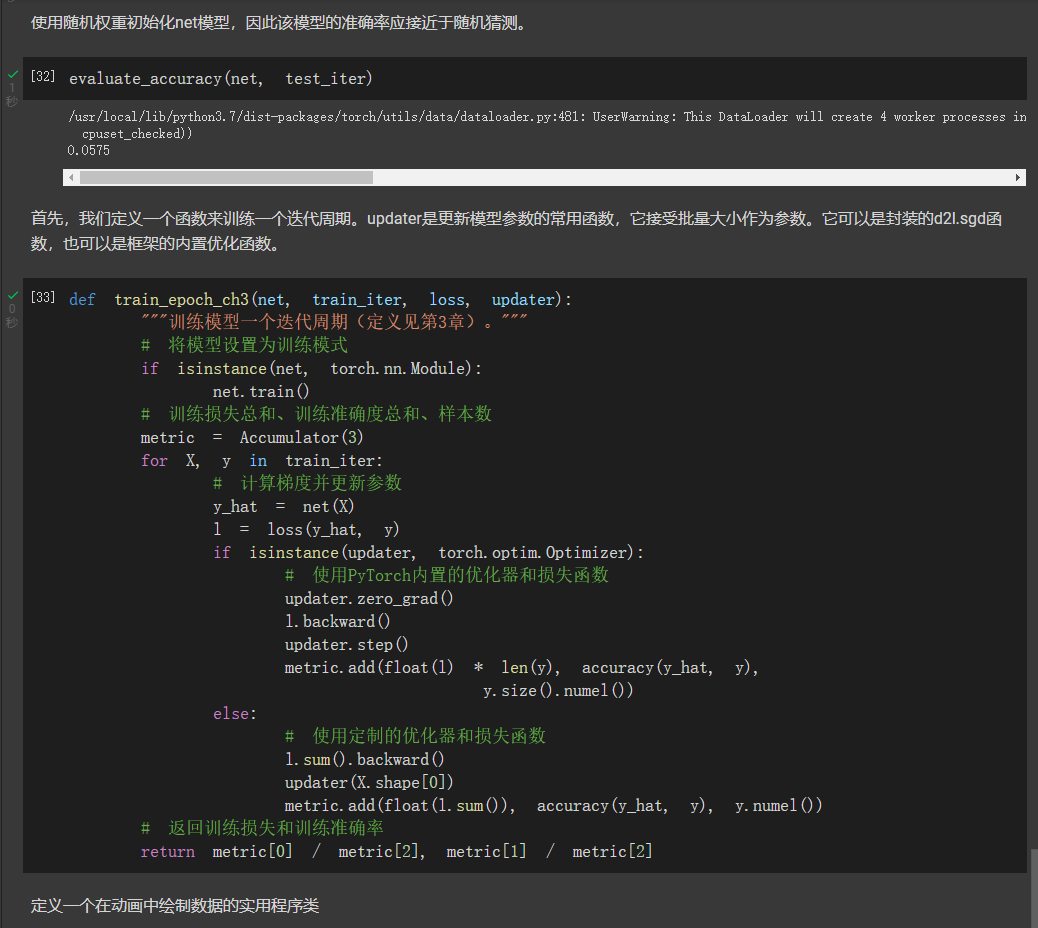
 定义 animator类略

 

 

 

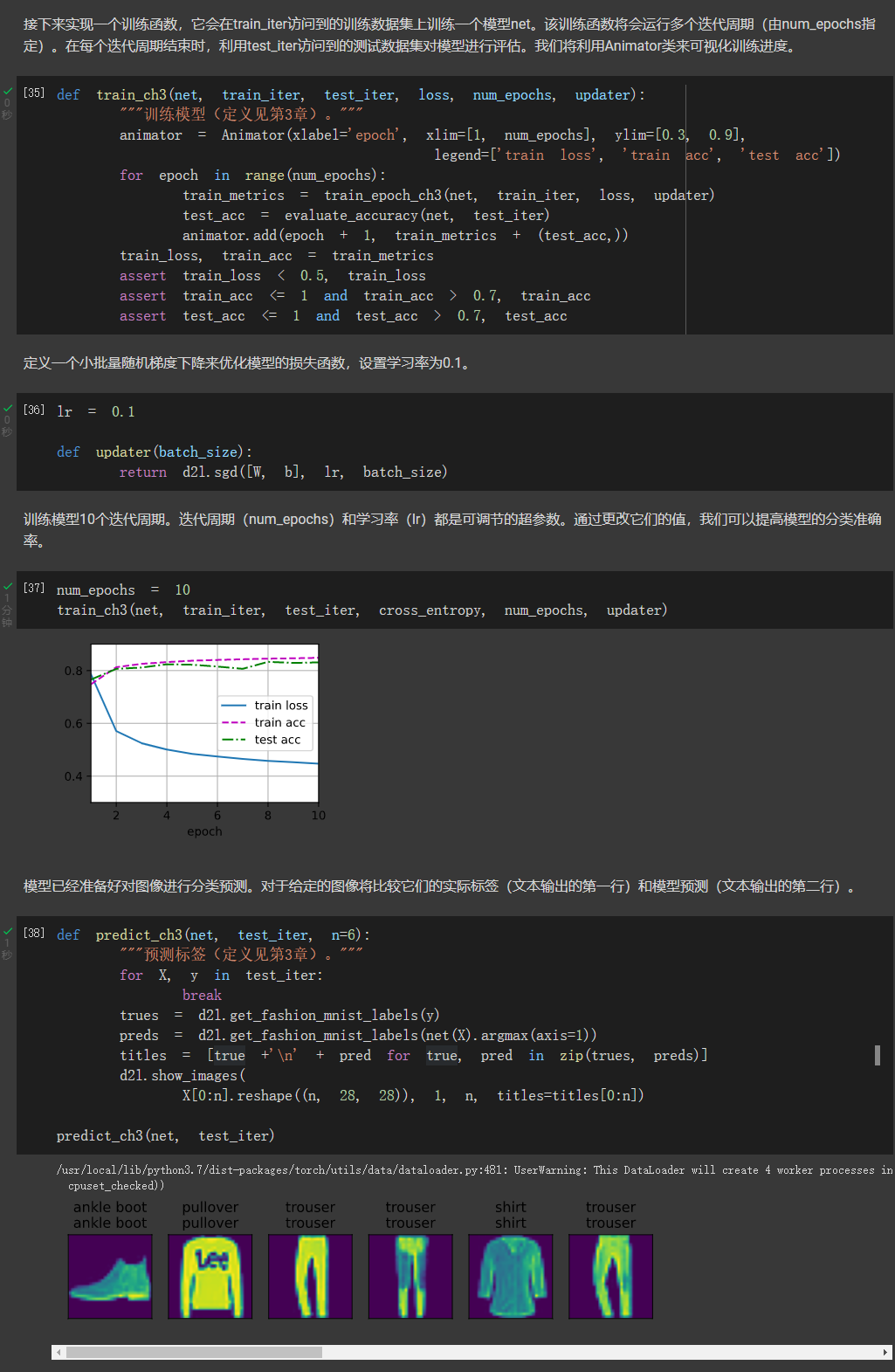
4.多重感知机

MLP由三层或更多层非线性激活节点组成(一个输入层和一个具有一个或多个隐藏层的输出层)。由于多层互连是完全连接的，所以一层中的每个节点都以一定的权重 w_ij 连接到下一层的每个节点。隐藏层得大小是超参数，可以设置。为了不使多层感知机退化成线性模型，引入了激活函数得概念。有了激活函数，多重感知机就不可能再退化成线性模型。

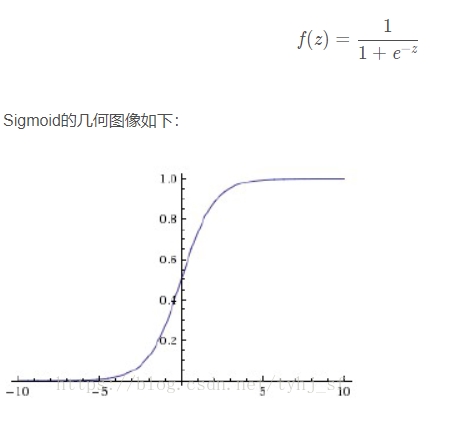
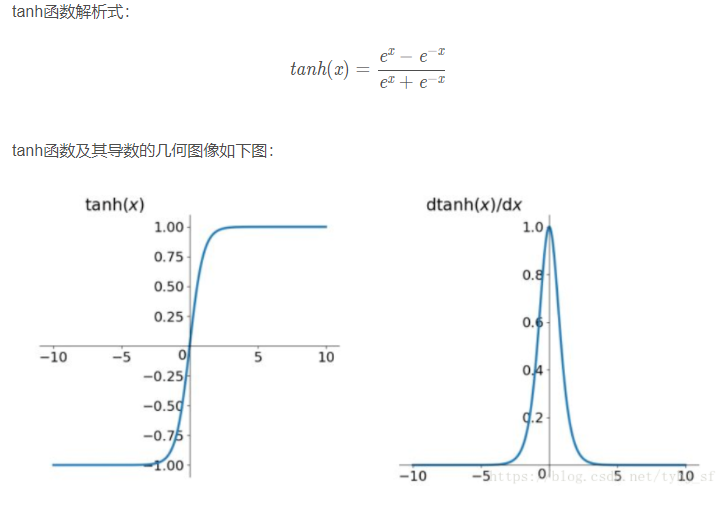
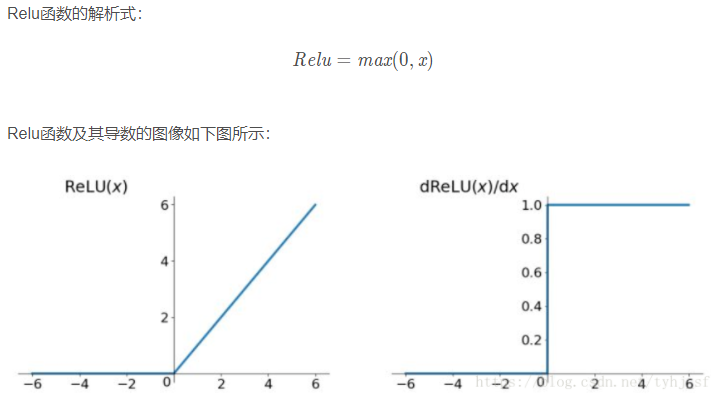
常用的激活函数包括ReLU函数、sigmoid函数和tanh函数。

 

 

 

 

 模型选择、欠拟合和过拟合

训练误差（training error）：我们的模型在训练数据集上计算得到的误差。

泛化误差（generalization error）：当我们将模型应用在同样从原始样本的分布中抽取的无限多的数据样本时，我们模型误差的期望。

数据集又分为训练数据集、验证数据集、测试数据集。

注：验证数据集不能和训练数据集混在一起。测试数据集只能用一次（代表未来发生的事件）

K折交叉验证：当训练数据稀缺时，我们甚至可能无法提供足够的数据来构成一个合适的验证集。这个问题的一个流行的解决方案是采用K折交叉验证。这里，原始训练数据被分成K个不重叠的子集。然后执行K次模型训练和验证，每次在K−1个子集上进行训练，并在剩余的一个子集（在该轮中没有用于训练的子集）上进行验证。最后，通过对K次实验的结果取平均来估计训练和验证误差。

 

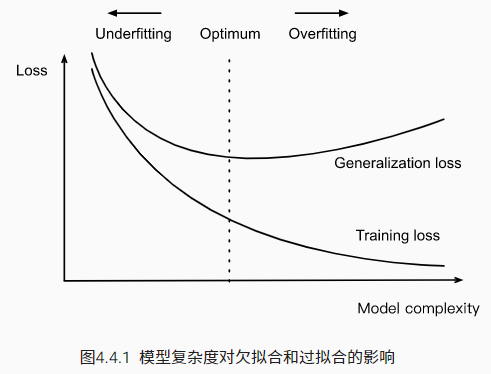
欠拟合和过拟合

欠拟合：模型无法继续减少训练误差。

过拟合：训练误差远小于验证误差。不能基于训练误差来估计泛化误差，因此简单地最小化训练误差并不一定意味着泛化误差的减小。机器学习模型需要注意防止过拟合，来使得泛化误差最小。

 

 

 

 权重衰减

权重衰减：主要用来处理过拟合。

正则化是处理过拟合的常用方法。在训练集的损失函数中加入惩罚项，以降低学习到的模型的复杂度。

保持模型简单的一个特别的选择是使用L2L2惩罚的权重衰减。这会导致学习算法更新步骤中的权重衰减。

 

数值稳定性和模型初始化

梯度消失和爆炸是深度网络中常见的问题。在参数初始化时需要非常小心，以确保梯度和参数可以得到很好的控制。

需要用启发式的初始化方法来确保初始梯度既不太大也不太小。

ReLU激活函数缓解了梯度消失问题，这样可以加速收敛。

随机初始化是保证在进行优化前打破对称性的关键。

Xavier初始化表明，对于每一层，输出的方差不受输入数量的影响，任何梯度的方差不受输出数量的影响。

 

 

补充：

本周由于课程较多，学习的课程没有衔接上，感觉本周的内容明显比上周要多，还需要消化一下本周的知识，本周任务没有完全完成，后面的报告写的有些匆忙没有完全写好，之后会和kaggle比赛代码完成后，一起补充上。