UVA 12716 GCD等于XOR[数学][提高+/省选-]
UVA 12716 GCD等于XOR[数学] [提高+/省选-]
输入数据组数t,
接下来t行每行给定一个数字n,
如样例所示格式输出
满足\(1 \le b \le a \le n\)且\(gcd(a,b)==a \oplus b\)的\((a,b)\)二元组个数。
in
2
7
20000000
out
Case 1: 4
Case 2: 34866117
思路
首先想想暴力
也就是 if(gcd(a,b)==a^b)ans++
枚举每一个 \(a\) 和 \(b\)
然后进行判断 这样的时间复杂度是 \(O(n^2)\)的
看了看数据范围只能作罢
那么如何去优化呢
设\(gcd(a,b)=a \oplus b= c\)
根据异或的交换律我们可以知道
\(a \oplus b= c , a \oplus c= b\)
因为\(gcd(a,b)= c\)
所以 \(c\) 一定是 \(a\), \(b\) 的因子
那么我们可以枚举 \(a\) 的因子\(c\)
那么 \(b\) 就是\(a \oplus c\)
再验证 gcd(a,b)是否等于 \(c\)
这样的时间复杂度是 \(O(nlog^2n)\) 的
已经可以解决这道问题了
那么还有没有更好的方法呢
通过观察我们可以发现
当 \(n\) = 7时
有4对成立 (3,2) (5,4) (6,4) (7,6)
我们发现 当\(gcd(a,b)==a \oplus b\) 时,总有 \(a-b=gcd(a,b)\) 成立
那么是不是总有这个规律呢
我们还是设 \(c\) 是 \(a \oplus b\) 和 \(gcd(a,b)\) 的结果
我们可以证明 $a-b \le a \oplus b $ (如不了解可以看文末)
又因为 \(c\) 是 \(a\) 和 \(b\) 的最小公因数
那么由辗转相除法我们可以类推出
\(gcd(a,b)\) \(\le\) \(a-b\)
也就是
\(gcd(a,b)\) \(\le\) \(a-b \le a \oplus b\)
又 \(c\) = \(a \oplus b\) = \(gcd(a,b)\)
也就是
\(c\) \(\le\) \(a-b \le c\)
也就是 \(a-b = c\)
也就是 $a-b = a \oplus b $
由于 gcd() 函数的时间复杂度 是\(O(logn)\)
\(\oplus\)的时间复杂度 是\(O(1)\)
那么我们只需要判断 \(a\)减去一个因子等不等于异或上这个因子
整个问题便变成了 \(O(nlogn)\) 的时间复杂度了
key code
const int N=3e7+10;
int n,m;
int ans[N];
int __;
void solve(){
//try it again.
cin>>n;
cout<<ans[n]<<endl;
}
signed main(){
IOS;
int k=N>>1;
fup(b,1,k){
for(int a=b+b;a<=N;a+=b){
if((a^b)==a-b){
ans[a]++;
}
}
}
up(2,N)ans[o]+=ans[o-1];
cin>>__;
up(1,__){
cout<<"Case "<<o<<": ";
solve();
}
return 0;
}
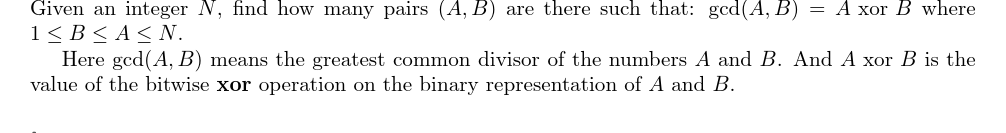
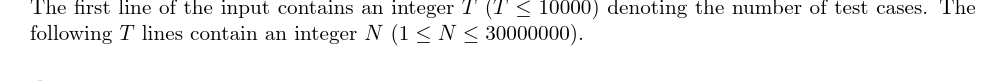

证明 $a-b \le a \oplus b $
当 $ a $ 是 1010 1111 ,$ b $ 是 1010 1111
这样的时候
此时 \(b\) 的每一位都在 \(a\) 的二进制上实现了相应的减法
也就是 $a-b = a \oplus b $ 的情况
如果有一位 \(a\) 与 \(b\) 不相等的话
那么 \(b\) 的那一位便会在 \(a\) 上实现相应的加法
也就是 $a-b < a \oplus b $ 的情况
不存在 $a-b > a \oplus b $ 的情况



 浙公网安备 33010602011771号
浙公网安备 33010602011771号