非确定性有穷状态决策自动机练习题Vol.1 题解 & 总结

前言

今天的成绩真就像下午老姚念总结的时候的那个同学一样，昨天刚刚考好一次，今天就又掉了......

下午找学长调昨天的T3，Jombo学长对着我的5.4k的代码和毒瘤的码风都要抓狂了，先立一个flag，以后要改变一下码风，至少找别人调代码的时候可以让别人稍微舒服一些。

今天下午好像来了一位新的学长，貌似是老师先前提到的来给我们讲数学的ckq学长？

快要放假了，今天下午机房里面颓废的风气好重......

扭动的回文串

 

 

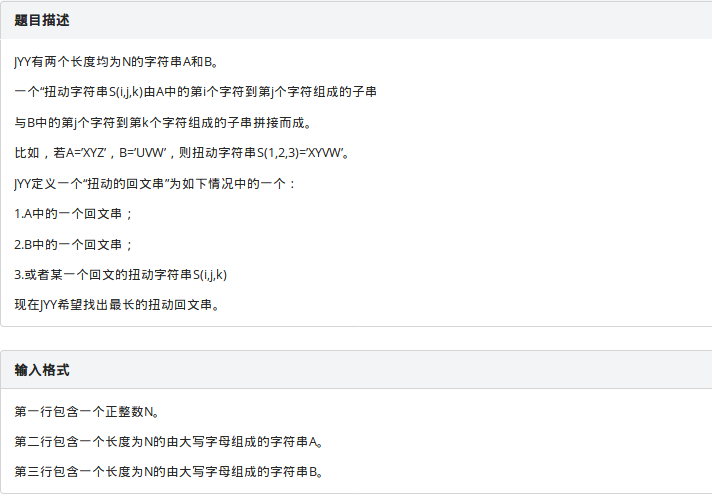
不知道上午大家考试的时候有没有读懂题，反正我当时是没有，于是去对面吵醒了还没起床的两位学长才搞懂题意......

做这个题首先我们要先发现一个规律，我们的答案一定是一个回文串的左右(其实是上下，即若取a串的回文串，在a的左边，b的右边再选取一些点)又放了一些对称的字符，而这个回文串一定是以当前回文串的中心为中心的最长的回文串，我们可以这样想，如果我们存在一种答案，使得回文串不是以当前回文串的中心为中心的最长的回文串，那么我们把答案变为回文串的中心为中心的最长的回文串结果一定不会更坏，而且这样方便我们查找，于是我们就可以枚举a的每一个点作为中心，在当前最长的回文两边二分查找另外延伸的字符串，哈希判断是否合法，就可以了，一交上去，73分，原因是我们需要再次以b串的回文串为基准计算一次，这样就没有问题了(学长讲课最后一句:难写难调)

 

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<ctime>
#include<cmath>
const int N=3e5+10;
typedef unsigned long long ull;
char a[N],b[N];
int da[N],db[N],ans,pos;
int n;
int mlc(char *cc,int *d){
    int len=strlen(cc+1);
    memset(d,0,sizeof(d));
    int c=0,r=-1,Max=0;
    for(int i=1;i<=len;++i){
        if(i > r) d[i]=1;
        else d[i]=std::min(r-i+1,d[2*c-i]);
        while(i-d[i] >= 1 && i+d[i] <= len){
            if(cc[i-d[i]]==cc[i+d[i]])
                d[i]++;
            else break;
        }
        if(i+d[i]-1 > r){
            c=i;
            r=i+d[i]-1;
        }
        if(d[i] > Max) Max=d[i];
    }
    return Max-1;
}
ull bas=233,ha[N],hb[N],mi[N];
bool Judge(int pos,int lb,int rb){
    ull haha=ha[lb]-ha[pos-1]*mi[lb-pos+1];
    ull hahb=hb[rb]-hb[rb+lb-pos+1]*mi[lb-pos+1];
    return haha==hahb;
}
int main(){
    freopen("A.in","r",stdin);
    freopen("A.out","w",stdout);
    scanf("%d",&n);
    n=n*2+1;
    mi[0]=1;
    for(int i=1;i<=n;++i){
        if(i & 1) a[i]='#';
        else scanf(" %c",&a[i]);
        mi[i]=mi[i-1]*bas;
    }
    for(int i=1;i<=n;++i){
        if(i & 1) b[i]='#';
        else scanf(" %c",&b[i]);
    }
    ans=std::max(ans,mlc(a,da));
    ans=std::max(ans,mlc(b,db));
    for(int i=1;i<=n;++i){
        ha[i]=ha[i-1]*bas+a[i];
    }
    for(int i=n;i>=1;--i){
        hb[i]=hb[i+1]*bas+b[i];
    }
    for(int i=1;i<=n;++i){
        int l=1,r=i-da[i];
        while(l <= r){
            int mid=(l+r)>>1;
            if(Judge(mid,i-da[i],i+da[i]-2)) r=mid-1;
            else l=mid+1;
        }
        ans=std::max(ans,da[i]-1+i-da[i]-l+1);
    }
    for(int i=n;i>=1;--i){
        int l=1,r=i-db[i]+2;
        while(l <= r){
            int mid=(l+r)>>1;
            if(Judge(mid,i-db[i]+2,i+db[i])) r=mid-1;
            else l=mid+1;
        }
        ans=std::max(ans,db[i]-1+i-db[i]-l+3);
    }
    printf("%d\n",ans);
    return 0;
}

 

^_^

 

 

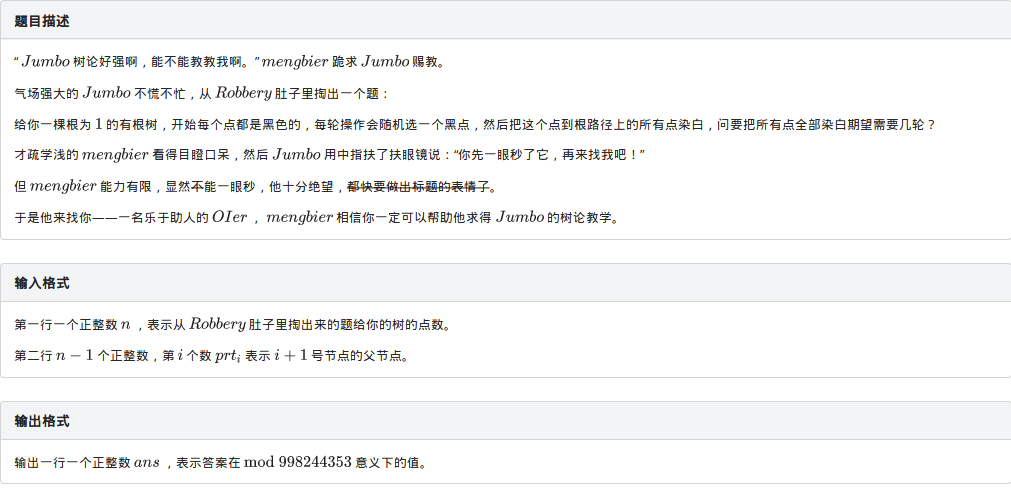
 这题不就是还在校的两位学长的互黑并且还拉上了刚走的robbory学长吗其实这道题并不怎么难,只是考场上我一看到期望就直接害怕了，就没有详细去想，其实这道题和学长昨天晚上讲的例题挺像的，就是反了一下，我们只需要求出每个节点的子树大小的逆元就OK了，考完试之后5min就改出来了......希望自己下次看到这类题目至少可以认真思考一下吧。

 

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
const int N=2e7+10;
const int Mod=998244353;
typedef long long ll;
ll ny[N];
void getny(int x){
    ny[1]=1;
    for(int i=2;i<=x;++i){
        ny[i]=(long long)(1ll*(Mod-Mod/i)*ny[Mod%i])%Mod;
    }
}
struct Node{
    int next,to;
}edge[N];
int Head[N],tot;
void Add(int x,int y){
    edge[++tot].to=y;
    edge[tot].next=Head[x];
    Head[x]=tot;
}
int siz[N];
void dfs(int u,int pa){
    siz[u]=1;
    for(int i=Head[u];i;i=edge[i].next){
        int v=edge[i].to;
        if(v==pa) continue;
        dfs(v,u);
        siz[u]+=siz[v];
    }
}
int main(){
    freopen("B.in","r",stdin);
    freopen("B.out","w",stdout);
    int n;
    scanf("%d",&n);
    getny(n);
    for(int i=1;i<n;++i){
        int x; scanf("%d",&x);
        Add(x,i+1);
        Add(i+1,x);
    }
    dfs(1,1);
    long long ans=0;
    for(int i=1;i<=n;++i)
        ans=(ans+ny[siz[i]])%Mod;
    printf("%lld\n",ans);
    return 0;
}

 

第K大区间

刚刚看到这道题的时候一直以为需要分块维护区间众数，于是最初的思路一直在想如何团出来一个根号的时间复杂度能过的方法，后来突然发现这不就是前几天考的原题吗，只是k小变成了众数，之后一直在想方法是否适用，拍了一下发现能过。于是就过了这道题(不开longlong见祖宗QAQ)

于是我们可以二分答案，检验答案的时候弄一个双指针，移动过程中维护数字的出现个数使得当前区间里面的数字的出现次数都小于等于二分出的答案，其实维护过程只要使得新加入的点的个数小于答案就可以了，毕竟维护之前的数列的每一个数字都是小于答案的，破坏这一现状的只能是新加入的数字，由于数字很大，需要离散化(map常数巨大会直接挂掉)于是我们就可以用nlog²的时间复杂度来过掉这道题了。(%%%用nlog的方法A掉这道题的大佬们 orz)

#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
const int N=2e5+10;
int a[N],b[N],cnt[N],n,k,tot;
int read(){
    int s=0,f=1;
    char ch=getchar();
    while(ch < '0' || ch > '9'){
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch >= '0' && ch <= '9'){
        s=(s<<1)+(s<<3)+(ch^48);
        ch=getchar();
    }
    return s*f;
}
bool Judge(int x){
    memset(cnt,0,sizeof(cnt));
    int L=1,ret=0;
    for(int i=1;i<=n;++i){
        int pos=std::lower_bound(b+1,b+tot+1,a[i])-b;
        cnt[pos]++;
        while(cnt[pos] > x){
            int now=std::lower_bound(b+1,b+tot+1,a[L])-b;
            cnt[now]--;
            L++;
        }
        ret+=i-L+1;
    }
    return ret >= k;
}
signed main(){
    freopen("C.in","r",stdin);
    freopen("C.out","w",stdout);
    n=read(); k=read();
    for(int i=1;i<=n;++i){
        a[i]=read();
        b[i]=a[i];
    }
    k=n*(n+1)/2-k+1;
    std::sort(b+1,b+n+1);
    tot=std::unique(b+1,b+n+1)-b-1;
    int l=1,r=n;
    while(l <= r){
        int mid=(l+r)>>1;
        if(Judge(mid)) r=mid-1;
        else l=mid+1;
    }
    printf("%lld\n",l);
    return 0;
}

收集邮票

 

 概率题是真的神仙这道题我们可以定义f，g两个数组，f[i]表示当前买了i种邮票购买完成需要的期望次数，g[i]表示当前买了i种邮票之后购买完成的期望花费，显然f[n]=g[n]=0，之后他们的转移就满足(juruo不会markdown，图片来自https://www.luogu.com.cn/blog/league/solution-p4550)：

 

 

 

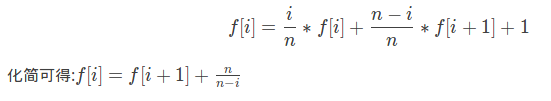
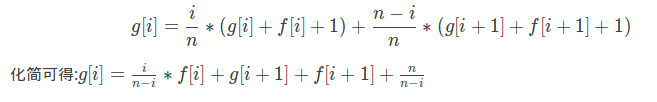
关于f的式子好理解，关于g的式子我们可以理解为倒着来计算，最后一次话费为f[i]，次小为f[i]-1一直到i为1，于是我们就可以把式子理解为前缀和的样子，每一次递推都从当前位置开始向后累加，到了1号节点之后就已经满足第k次花费为k的条件了，于是最后的答案就是g[n](代码真短)

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n;
double f[N],g[N];
int main(){
    freopen("D.in","r",stdin);
    freopen("D.out","w",stdout);
    scanf("%d",&n);
    for(int i=n-1;i>=0;--i){
        f[i]=f[i+1]+(1.0*n)/(1.0*(n-i));
        g[i]=(1.0*i)/(1.0*(n-i))*(f[i]+1)+g[i+1]+f[i+1]+1;
    }
    printf("%.2lf\n",g[0]);
    return 0;
}