BUAA OO 第一单元总结
BUAA OO 第一次作业总结
第一次作业
任务介绍
第一次作业是简单的单变量多项式展开,括号嵌套最多一层,支持加,减,乘,乘方运算。
UML图与类结构
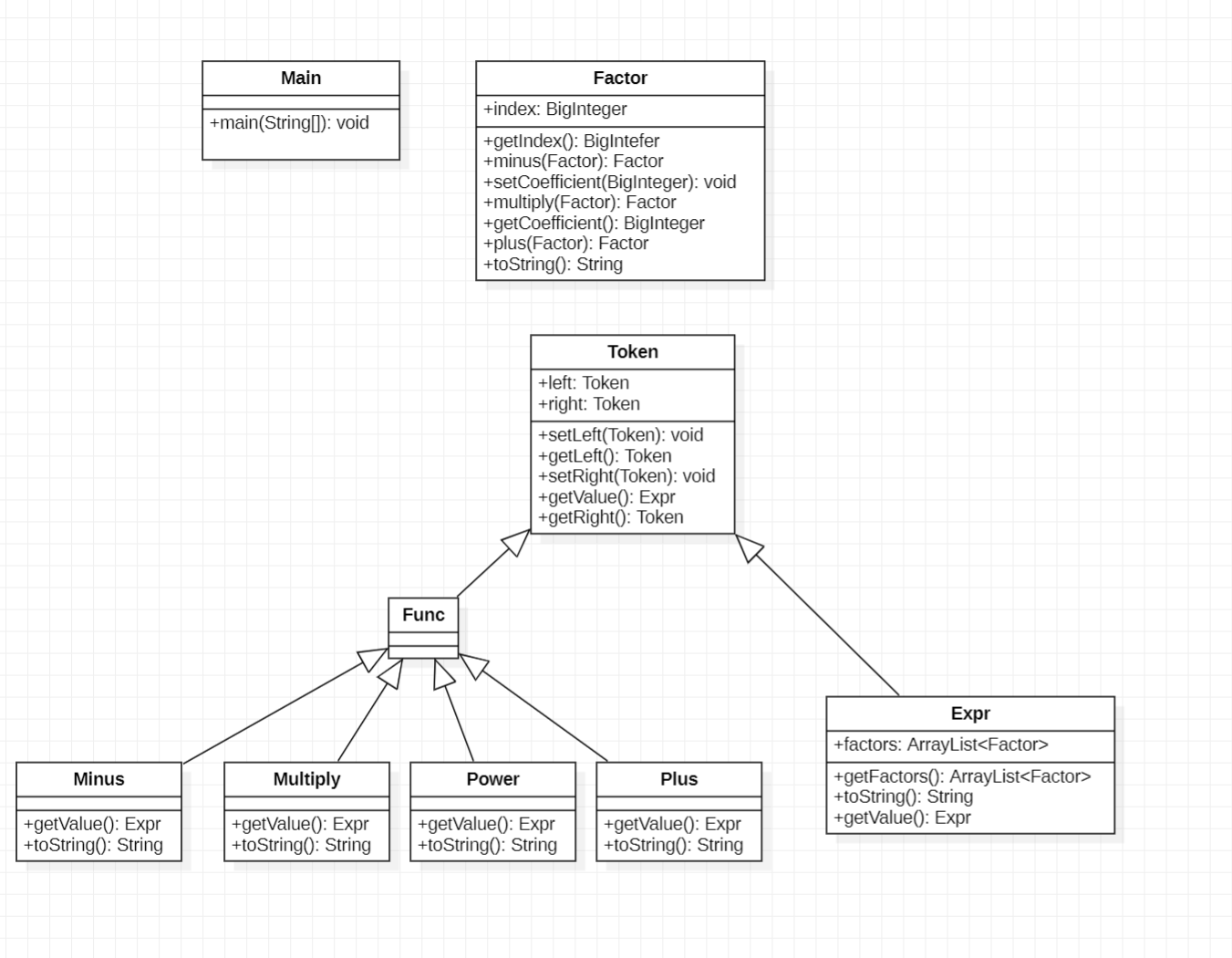
架构分析
整体程序分为三个部分,parser用于对输入进行解析同时建立表达式树,Expr和Factor作为实际维护数据的对象,Plus、Minus、Multiply和Power作为运算符号。Main作为主控类,Token作为数据和运算符号的父类,Func作为运算符号的父类。
设计理念
由于本次作业复杂度很低,十分类似程序设计课程中的表达式运算的题目,于是考虑使用栈来处理输入,将数据和运算符均作为节点来显式地构建表达式树。对于加、减、乘、乘方四种运算,按照乘方>乘>加减的优先级来作为入栈优先级,通过一个符号栈和一个节点栈来实现整个表达式树的建立。在最终输出时,调用根节点的getValue()方法即可递归地将全部式子运算。
化简方法
在维护数据的节点直接向上返回。在运算节点处,新开一个数据节点Expr,将左右节点的Factor依次运算并加入到Expr中,在加入之前遍历Expr内的Factor,查找是否存在可合并项。
度量分析
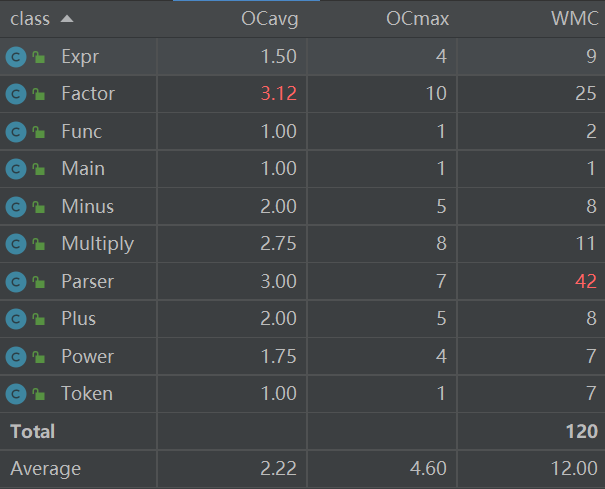
可以看到多数类的复杂度是可以令人满意的,对于parser类是由于在处理输入的过程中基本是按照面向过程的方法考虑的,由于这部分不会产生过多变化,所以也是可以接受的。
方法圈复杂度分析

大部分方法的复杂度都不算太高,对于Factor的toString方法由于在其中做了一些输出时化简的特判所以复杂度偏高,Multiply.getValue()的方法对于遍历左孩子右孩子的Factor并在其中做了一些判断所以导致复杂度偏高。
BUG分析
在进行乘法操作时,查找到可合并项后就直接合并,但是会出现合并后消项导致空项的产生。
HACK策略
利用递归下降生成随机数据,并调用sympy进行正确性检验。
边界数据的检验:零指数,乘值为零的多项式,多符号
心得体会
第一周由于一些别的事情导致没有花足够的时间在OO上。开始设计时考虑了过多的可扩展项如多变量的设计,求导运算,三角嵌套和非法判断等等,导致在架构设计上纠结了很久,最后决定这周实现一个暴力简单的版本下周重构。所以并没有考虑很多扩展性的问题。在组织数据上开始问题最大的是如何解析表达式,利用栈实现表达式树本质上还是一种面向过程的方法,运算和数据应该聚合在一起构成对象而不是单独抽离出来,这些在第二周的架构设计里均得到了改善。
第二次作业
任务介绍
本次作业加入了抽象表达式,三角函数和求和函数。
UML类图

架构分析
整个程序依旧分为三个部分,lexer和parser作为输入解析工具解析表达式,Expr、Term和Factor作为维护数据的对象,Substitute作为函数替换工具。
设计理念
整个程序实际上完成了三个步骤,解析输入,替换因子和表达式展开,分别对应上述的三个部分。其中,lexer作为词法分析器解析到每个词(数字,变量,函数符号,运算符和括号),parser作为语法分析器解析到Expr。在整个表达式中,运算是分为三个层级的,表达式层做加减运算,项层做乘法运算,因子层做乘方运算,这也决定了这三个类中的展开方法。最后说到替换因子,考虑到在自定义函数和sum函数中,只要将其中对应因子替换成为输入的因子即可得到函数的值,所以substitute方法的实现思路是,保持原来表达式的项不变,对项中的每一个因子做替换即可,只要将因子替换返回一个表达式因子即可消除掉所有的自定义函数和sum函数。最后在顶层调用表达式的去括号方法即可。
化简方法
这周侧重于重构架构了,没有进行特殊的优化,只是进行了简单的合并同类项。具体操作是,在Factor层和Term层均有乘法操作,在一个新的Factor加入到Term之前,先进行查找是否有可以直接指数相加的项,若有则直接指数相加,没有则放入Term的hashset中。在Expr层的加法操作中,在一个新的Term加入到Expr之前,先查找是否有可以直接相加的项,有则直接加,没有则将Term加入Expr中。一个需要注意的地方是,直接在hashset中修改元素,该元素会保有之前加入时的hashcode,举个例子来说,sin(x)^2 * cos(x) + sin(x)^2 * cos(x)有可能是无法合并的,因为sin(x)的指数可能是通过合并得到的,该项的hashcode可能是由sin(x) * cos(x)计算得到的,在新元素加入时,我们在进行是否能合并的判断时会先判断hashcode是否相等,那么在这种情况下即使两个项是equal的但却不会被判定为可合并的。正确的做法是将原来的项remove再将新的项add。
度量分析
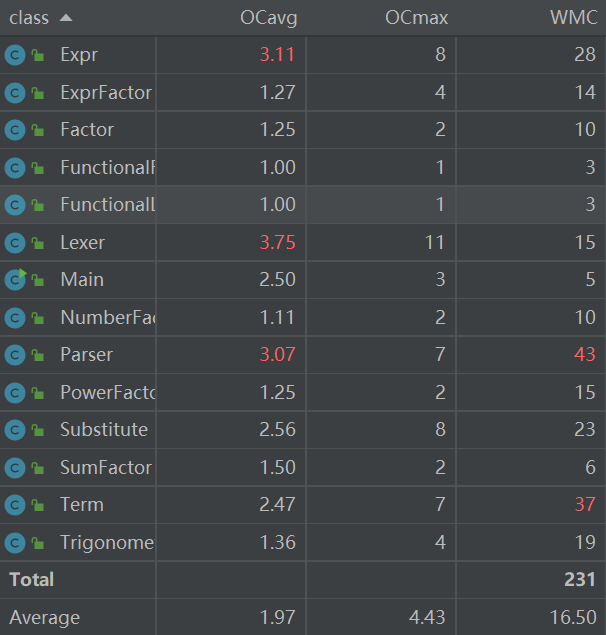
复杂度偏高的主要类是Parser和Lexer,这部分基本是按照面向过程的方法实现的所以会导致if分支很多,进而导致复杂度偏高 。
方法圈复杂度分析
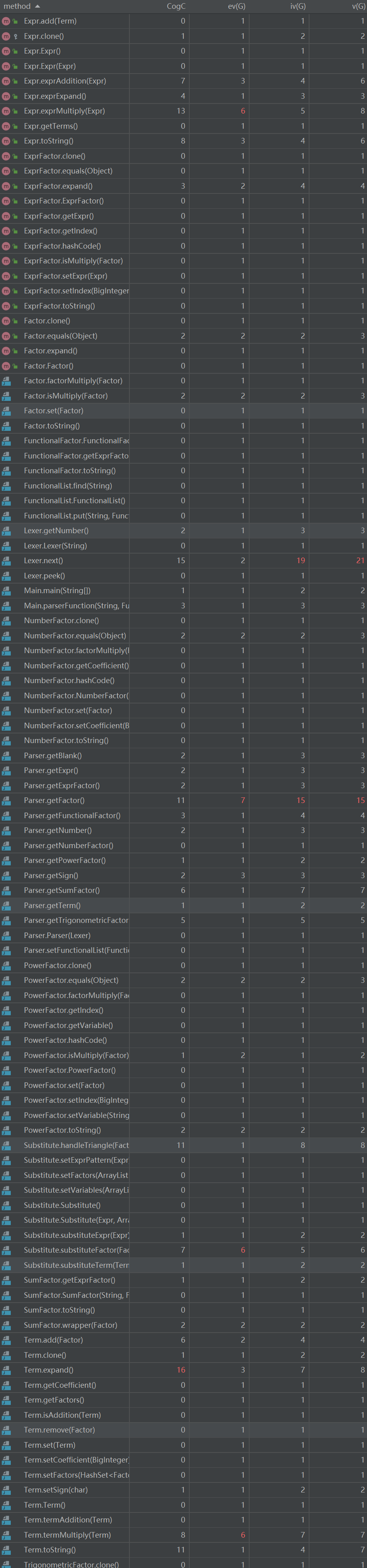
主要复杂度还是在于Parser和Lexer,原因同上。Term.expand()操作由于做了大量的类别判断所以复杂度偏高,更好的做法是单独再写一个用于处理对不同Factor加入策略的函数。
BUG分析
出现了一个十分不应该的bug。在解析sum函数中的start和end两个数字时直接调用了lexer.next获得了下一个词而忘记调用getNumber()去获取一个数字导致符号被忽略了。出现该bug的原因也和在测试时重点测试了运算步骤是否正确,而忽视了数据的解析测试。
HACK策略
本次hack测试重点放在了三角函数的测试上。测试样例类型主要有大面积的随机数据的测试,对三角函数合并的测试和三角函数带括号和指数的测试等。
第三次作业
任务介绍
本次作业增加了括号嵌套和自定义函数的嵌套
UML类图
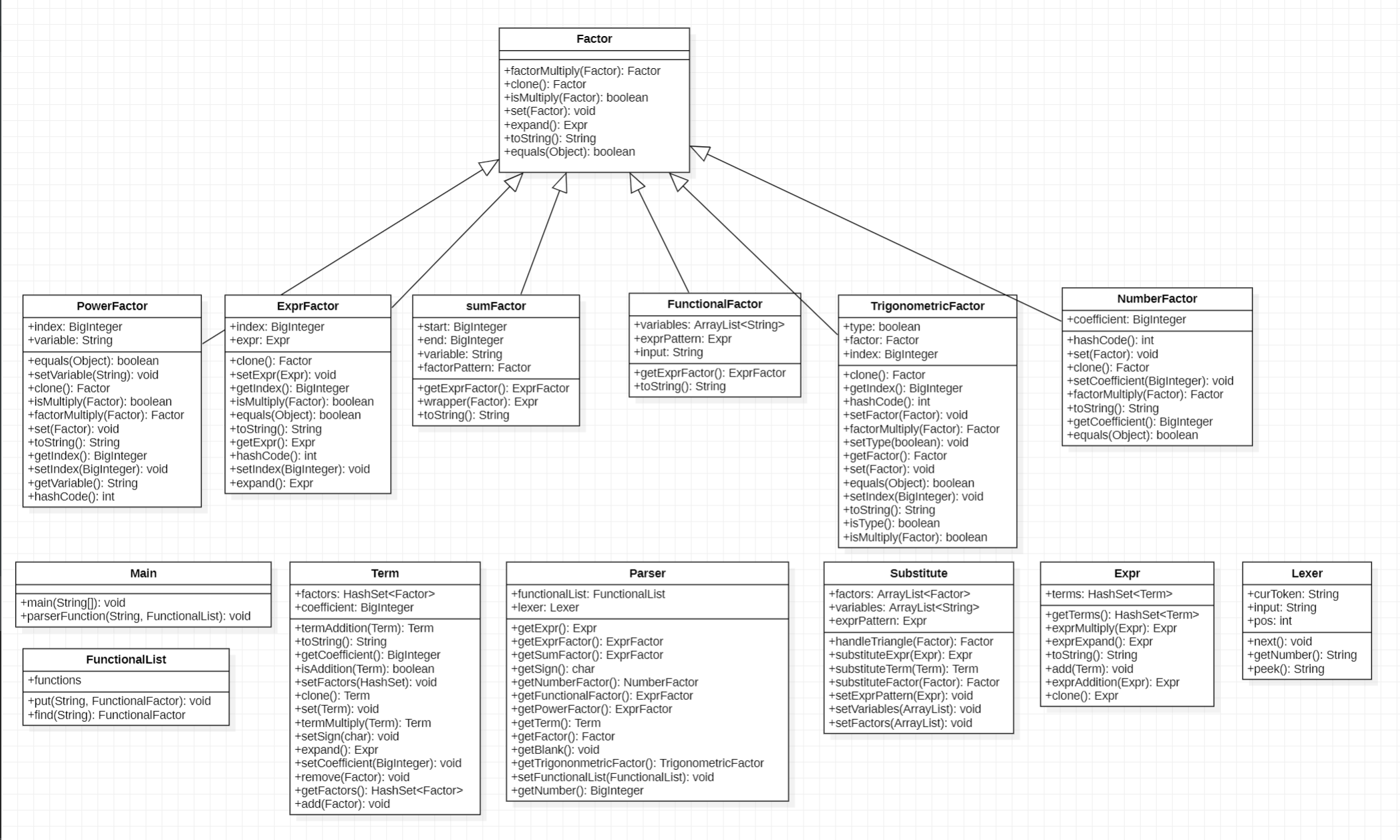
架构分析
本次作业和上次的架构一致,只需要修改substitute对于三角因子的实现即可(上次的因子更为简单于是直接做了特判)。
化简方法
开始秉承着不化简就不会错的原则一直没有化简。最终觉得加上化简操作也没有太大工作量于是就做了部分优化。优化有三个部分,首先是sin(0)和cos(0)的优化,这部分只需要判断三角函数里Factor的类型并返回相应的三角因子或者数字因子即可。第二部分是sin(x)**2 + cos(x)**2 = 1的优化。这部分需要在项的加减合并中多加一条合并规则,即当两个项的系数相同,因子只有一项不相同且符合上述合并规则的则加以合并。第三部分是二倍角的优化。这部分需要在因子合并部分多加入一条合并规则,即当两个因子为可合并的三角因子,并且其所在项的系数满足合并要求时则可以合并。不过实际上第三部分做的并不理想,因为对于第二部分的合并来说,应该采取贪婪的合并策略,即在运算过程中应该尽可能做第二部分的合并。而对于第三部分的合并策略则应该是非贪婪的,举个例子,对于2*sin(x)*cos(x) + sin(x)*cos(x) ,如果提前合并会导致sin(x)*cos(x) + sin((2*x))的结果。应当在全部合并完成后再对表达式进行一次遍历寻找二倍角的合并机会。
度量分析
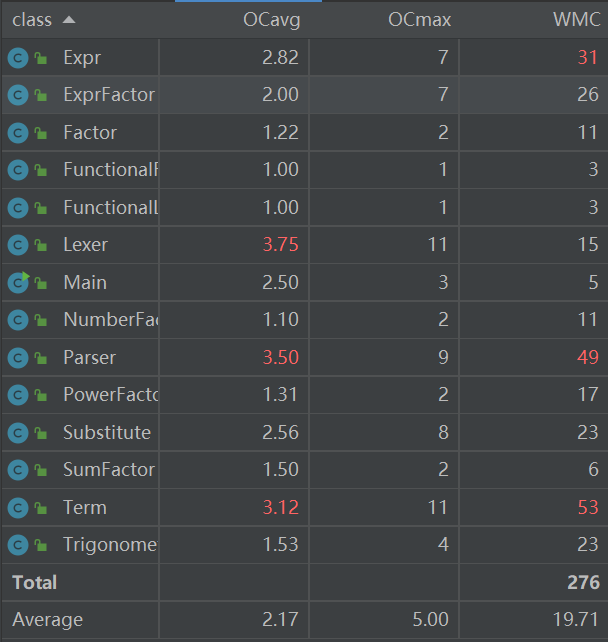
方法圈复杂度分析

大体与上周相同,只是在Term层级的合并部分的方法复杂度偏高,原因是在做优化的过程中引入了大量特殊情况判断,这些判断之前嵌入在了合并过程中,更好的做法是将优化部分单独抽出来写一个函数来实现。
BUG分析
本次作业没有找到bug(但悲剧的是最后一版忘交了...请一定做好版本管理!!)
HACK策略
个人互测的重点是对sum函数的测试,主要有爆int,sum和其他函数的组合嵌套,sum的上下限测试等,以及朴素的大规模随机数据的测试。
心得体会和经验总结
经验总结:
- 提前做pre收悉java的编程模式
- 对架构的设计要规划长远,尽量选择更加通用的方法,比如自定义函数中不建议使用字符串替换
- 自动测评很重要!!!
心得体会:
- 对面向对象编程模式的了解,体会到设计数据结构和行为的重要性。
- 在写程序之前一定要做好设计工作,即使不实现具体功能也可以提前设计数据结构和接口模式。
- 了解了一些设计模式如与本次作业结合紧密的工厂模式,以及其他模式如单例模式,生产者消费者模式等等。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号