第二讲 Learning to Answer Yes/No

Perceptron Hypothesis Set (感知机模型)

感知机：解决线性分类问题

问题：已经有过去银行对不同客户发放信用卡情况的数据，判断是否给顾客信用卡（发/不发：二值问题）。

思路：将顾客的所有信息（如：收入、负债等个人信息）作为特征输入，给不同的特征设立权重，最后根据所有的特征乘上各自对应的权重的和是否超过设定值来决定是否给顾客发信用卡。可以理解为考试中给每道题设定分值，最后总分值是否超过60分来判断是否及格。

定义顾客特征信息定义为向量$（x_1,x_2.....x_d）$，各自对应的权重值$(w_1,w_2......w_d)$，门槛值（threshold）。

 

For x=$(x_1,x_2.....x_d)$ 'features of customer', compute a weighted 'score' and,

approve credit if  $sum_{i=1}^dw_i*x_i>threshold $

deny credit if  $sum_{i=1}^dw_i*x_i<threshold $

y:{+1(good), -1(bad)},0 ignored. Linear formula h $\in$ H are 

$ h(x) = sign((sum_{i=1}^dw_i*x_i) - threshold)\label{eq:set_fomula}$

$sign(x) = \begin{cases} 1, & \text{if }0<x; \\ 0, & \text{}x<0. \end{cases}$

 

所有满足该形式的模型均属于模型集合，而唯一辨识每个不同的模型的属性便是其中的不同特征对应的权重以及最后的门槛值。所以在此假设基础上如果想要得到一个模型则需要有一个演算法去找一个近似理想公式的模型公式。最后当演算法结束后可以得到一个模型，对于所有的输入资料均能通过该模型得到一个相同的分配结果（是否给予该顾客信用卡），当有一个新的顾客时便可将其对应的特征输入到模型中进行预测。

值得注意的是对于h(x) =$sign((sum_{i=1}^dw_i*x_i) - threshold)$，我们可以将形式进行统一：

 

h(x)=$sign((sum_{i=1}^{d}w_i*x_i) - threshold)$

=$sign((sum_{i=1}^{d}w_i*x_i) +\underbrace{\text{threshold}}_{w_0}*\underbrace{1}_{x_0})$

=$sign(sum_{i=0}^{d}w_i*x_i)$

=$sign(w^T*x)$

 

学过现行代数的大家就会知道我们把这些权重和特征表示成了两个列向量，最后的预测结果便是向量的内积的正负号，下面的演算法里大家会感受到这个向量表示的作用。

这样的描述很抽象，因此引入一种方式就是使用图像（或者可以说是几何）来更形象更具体的来说明以上函数。

为了理解方便将输入向量的维度限制为两个，即h函数可以表示成公式$h(x)=sign(w_0+w_1*x_1+w_2*x_2)$ 。将输入向量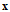对应于一个二维平面上的点（如果向量的维度更高，对应于一个高维空间中的点），输出y（在分类问题中又称作标签，label）使用○表示+1，×表示-1。假设h对应一条条的直线（如果在输入向量是高维空间的话，则对应于一个超平面）这里不同的权值w向量对应不同的直线，而sign(x)是以0为分界线的函数，所以可以设$w_0+w_1*x_1+w_2*x_2$，该式恰是一条直线的表示，注意其中的$(w_0,w_1,w_2)$为直线对应的法向量（规定法向量的方向指向正类所在一侧，后面的演算法可以验证该点）。而最后的结果便是从所有的模型中找到一条边满足每条边的一边为正的，而另一边为表示为负的。如下图右所示。

　　　　　　　　　　　　　　　　　　　　　　　　

 

Perceptron Learning Algorithm(PLA 感知机演算法)

 如果从上面二维的例子中，我们可以看到其实找模型便是从平面中找到一条直线能够无限接近最理想的线（可以理解为因为当前数据有限可能在后续数据更新的结果中会存在错误点，理想的线则是完美匹配现有数据和未来所有的数据），很朴素的想法便是随便先找一条线，然后去看这条线是否已经能够将当前资料情况进行有效划分，如果不行则至少有一个点不符合即$w_{t}*x_{n}\neqy_{n}$。

这里补充我的一个理解，就是大家其实可以注意到我们已知的$(w_0,w_1,w_2)$其实是该直线的法向量，（所有直线上的点所表示的向量和法向量相乘（内积）结果为0，说明垂直）。假设已经找到一条正确的线，而相应的法向量也已经得到，大家去观察这个法向量和其他分类点的连线可以发现，正类点和法向量的夹角<90，而负类点和法向量的夹角>90，也正是对应直线$w_{t}*x_{n}$的符号了，通过这个希望能帮助大家理解下面演算法中几何含义。

所以其实在求这条线的同时也可以看成要求这条线的法向量，下面的过程某种程度上大家可以理解成根据当前点和法向量之间的夹角关系来迭代更新法向量。

1.如果这个点是正点被划分为负点，即$w_{t}*x_{n}<0\ne y_{n}$，说明则说明该线和理想线的夹角大了，为了使得夹角减小，我们可以令$w_{t+1}=w_{t}+x_{n}$，即向量相加，可以看出夹角就变小了；
2.如果这个点是负点被划分为正点，即$w_{t}*x_{n}>0\ne y_{n}$，此时积大于0而本来应该是小于0，说明则说明该线和理想线的夹角小了，我们可以令$w_{t+1}=w_{t}-x_{n}$，即向量相减，尽量使夹角变大。

　　　　　　　　                                          

仔细观察以上操作，可以发现在需要修正的情况下，修正的操作（加上或减去向量）与本身的结果+1、-1一致，所以可以将以上操作定义一致化。

 

Cyclic PLA:

For t=0,1

　　find the next mistake of $w_t$ called ( $x_n(t),y_n(t)) as sign( $w_t^Tx_n(t)$) $\ne y_n(t)$

　　correct the mistake by

　　　　　　$(w_(t+1) = w_t + y_n(t)*x_n(t)$

.......until a full cycle of not encoutering mistakes

 

解释一下，这个算法起初是从零向量为权重向量（法向量），然后逐渐去修正，修正的过程中逐一以圈的形式去和已知数据中的特征值（分类点向量）内积，根据内积结果和最终结果一致性修正向量，而只有当特征值完整地从头到尾运算一遍后没有出过错误才说明找到了目标结果可以停止运算，否则会循环从头再来一次修正。因此有Cyclic的说法，当然不一定说非要这样的遍历方式，你也可以先基数再偶数或者随机遍历，只要能够保证对每一个数据都公平即每一轮中每一个数据都遍历验证过。关于这个演算法的缺陷，如对噪点或非线性可分数据的情况在后面会提到解决方式。

还有一点需要注意到的是一次操作不一定能够修正一个点上的错误，但是可以通过多次重复以上操作使得当前线更加趋近于理想线。

 

Guarantee of PLA（PLA演算法的保证）

对于PLA演算法，我们需要考虑它的可靠性，对此提出了以下问题：

1.PLA算法在线性可分的情况下一定会停下来吗？

2.对于噪点即一堆正常数据中混淆一小部分错误数据如何解决？

3.非线性可分？

 

对于1.PLA算法是如何确定在线性可分的情况下一定会停下来.

定义：t：当前迭代至t轮，此时的权重为$w_t(t)$，已有特征数据和结果数据为($x_n，y_n$)

条件：

线性可分即存在理想线或者说理想权重可完美处理划分情况，定义为$w_f$，有$y_n*w_f*x_n\lq 0$

只有在存在错误时才会进行修正，即$w_t*x_n\nq y_n$即$y_n*w_t*x_n<0$

思路：由于我们是要找到一条线去趋近于理想线，假设会停下来我们可以猜想这条线应该是要越来越接近理想线，首先我们先看下内积，

 

$w_f^T*w_{t+1}=w_f^T*(w_{t}+y_n*x_n)$

$\le w_f^T*w_t + min_n y_n*w_f*x_n $

$\le t*min_n y_n*w_f*x_n$

 

已知$min{y_n*w_f*x_n}>0$，所以$w_f^T*w_{t+1}$越来越大，理论上很像我们猜想的越来越接近目标向量，但是内积我们要注意到，其中还有$\|w_{t+1}\|$的模作为影响因子不能完全把内积的值的增加全部当成是角度的贡献，那下面我们再看下$\|w_{t+1}\|$的变化。

 

$\|w_{t+1}\|^2=\|w_t+y_n*x_n \| ^2$

=$\|w_t\|^2+\|y_n*x_n\|^2+2*y_n*w_t^T*x_n$

 

对于$y_n*w_t*x_n$，已知当前点是在错误的时候，即$w_t*x_n\ne y_n$即$y_n*w_t*x_n<0$

 

原式=$\|w_t\|^2+\|y_n*x_n\|^2+\underbrace{2*y_n*w_t^T*x_n}_{<0}$

<$\|w_t\|^2+\|y_n*x_n\|^2$

<$\|w_t\|^2+max_n \|y_n*x_n\|^2$

<$T*max_n \|y_n*x_n\|^2$

 

可以注意到向量的模的增加由于有一个负因子限制着不会让它增长太快，我们最后将上述两个式子结合一下通过正规化观察下：

 

　　$\frac{w_{t+1}}{\|w_{t+1}\|}*\frac{w_f}{\| w_f \|}$

     >$\frac{t*\min_n y_n*w_f*x_n}{\|w_f\|*\sqrt{t*max_n \y_n*x_n\|^2}}$

     >$\sqrt{t}*\frac{\min_n y_n*w_f*x_n}{\|w_f\|*\sqrt{\max_n \|y_n*x_n\|^2}}$

     =$\sqrt{t}*constant$

 

令$R^2=\max_n\|x_n\|$，$\rho=\min_ny_n*w_f*x_n$，则

     constant = $\frac{\rho}{R}$

注意到constant是一个常数，在这个过程中正规化的结果会随着t迭代轮数的增大而增大，又知道正规化后的内积其实便是cosA，A是两条线的夹角，这样的结果便很清楚的显示出了当迭代轮数的上升时趋近于目标结果，又知道两条直线最接近时便是二者重合，正规化内积为1，以此作为上限：

     $1\le \sqrt{t}*constant$

     $\frac{R^2}{\rho^2} \le t$

说明t迭代轮数是有上限，t又是整数，最终一定会停下来。

至此我们便通过正规化的内积结果证明到第t轮的向量随着迭代会越来越接近理想向量，而这个迭代轮数也是有上限的，最终一定会停下来，找到目标向量，演算法停止。

 

Non-separable Data（非线性可分数据）

但是很可惜现实生活中的数据不一定那么完美，比如我们提到的会出现噪点，如果我们按照上面的算法可能就会在某个点把近似完美的模型给毁了，或者说本身便不是线性模型能划分类。

 首先对于噪点，我们可以假设噪点的数量会远小于原来的正确数据量，在此情况下我们找出一条能最大程度上正确划分类的线，在上述算法过程中在发现错误点时观察修正后的结果是否能够修正后的正确划分点多于上一个正确划分点，如果可以，说明这条线更好，那就修正，然后在演算尽可能多的情况下停下来便认为这是一个不错的解。事实上这是一种贪心的算法。

Pocket Algorithm

modify PLA algorithm bykeeping best weights in pocket

For t=0,1

　　find the (random) mistake of $w_t$ called ( $x_n(t),y_n(t)$) as sign $w_t^Tx_n(t)$) $\ne y_n(t)$

　　correct the mistake by

　　　　　　$w_{t+1} = w_t + y_n(t)*x_n(t)$

　　if $w_{t+1}$ makes fewer mistakes than $w_t$ replace $w_t$ by $w_{t+1}$ 

.......until enough iterations

而对于其他非线性可分的数据，则需要用其他模型进行解决。