dp tricks

好多好杂，一个个放真的会炸掉。

决策单调性

四边形不等式

对 $w_{i,j}$，若 $\forall a \leq b \leq c \leq d,w_{a,d}+w_{b,c}\geq w_{a,c}+w_{b,d}$ ，则称 $w$ 满足四边形不等式关系，该不等式为四边形不等式。

几何意义

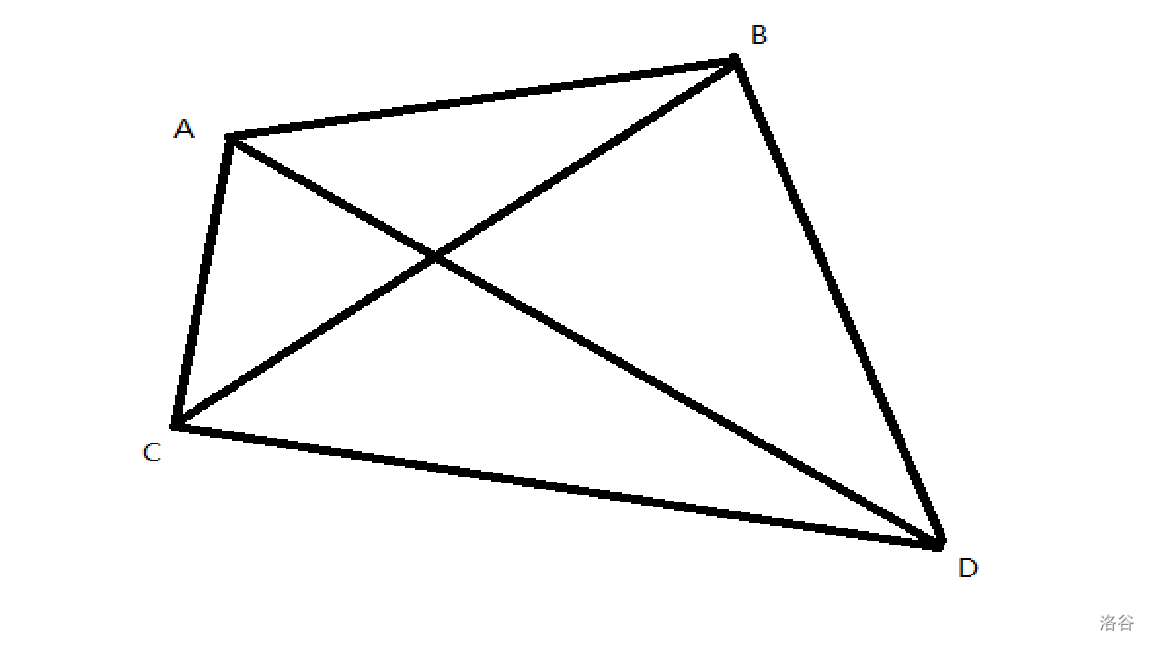
可以由三角形不等式证出凸四边形 $ABCD$ 中，$AD+BC \geq AB+CD$，这就是四边形不等式的几何意义。

性质：满足 $w_{i,j+1}+w_{i+1,j} \geq w_{i,j}+w_{i+1,j+1}$ 的 $w$ 满足四边形不等式关系。

证明：

记上式为（1）式。用 $i+1$ 改写（1）式，得到：$w_{i+1,j+1}+w_{i+1,j+1}\geq w_{i+1,j}+w_{i+2,j+1}$，记为（2）式。两式相加，得到：$w_{i,j+1}+w_{i+1,j} \geq w_{i,j}+w_{i+2,j+1}$；用 $i+2$ 改写（1）式，同理可得 $w_{i,j+1}+w_{i+3,j}\geq w_{i,j}+w_{i+3,j+1}$，以此类推，我们可以得到 $w_{a,c+1}+w_{b,c}\geq w_{a,c}+w_{b,c+1}$，我们用同样的方式就可以推出对 $a,b,c,d$ 不等式都是正确的，得证。

这个性质多用于证明 $w$ 满足四边形不等式关系，但我们一般打个表出来，观察到符合性质就直接写优化了。这并不严谨，但场上很好用。

优化 DP

一般地，四边形不等式用来优化形如 $f_{i}=\min/\max_{j=1}^{i-1}\{f_{j}+v_{j,i}\}$ 的 DP 转移。下面我们以 $\min$ 为例说明四边形不等式优化 DP 的过程。

我们引入决策的概念。$i$ 的决策点 $p_i$ 表示 $f_j+v_{j,i}$ 的最值取到的那个点，即 $\min\limits_{j=1}^{i-1}\{f_j+v_{j,i}\}=f_{p_i}+v_{p_i,i}$。考虑如何利用决策点与四边形不等式的性质进行优化。

性质1：若 $v$ 满足四边形不等式关系，则决策点单调。

证明：反证法。若决策点不单调，即存在 $c,d$ 使 $b=p_c > p_d=a$，此时 $a < b \le c < d$，根据最优化条件，$v_{a,d} \leq v_{b,d}$ 且 $v_{a,c} > v_{b,c}$，故 $v_{a,d}-v_{b,d}\le 0 < v_{a,c}-v_{b,c}$，与四边形不等式矛盾。$\square$

性质2：若有 $x<j$，存在 $i>j$ 使 $j$ 比 $x$ 更优，则对于 $i' > i$，取 $j$ 比 $x$ 同样更优。观察到性质1这条性质的特例。一定要注意 $x<j$ 这个条件。

证明：由题意得 $f_{x}+v_{x,i} > f_j+v_{j,i}$，

由四边形不等式有 $v_{x,i'}+v_{j,i}> v_{x,i}+v_{j,i'}$

移项得 $v_{x,i'}-v_{x,i}>v_{j,i'}-v_{j,i}$

与第一个式子相加，得 $f_x+v_{x,i'}>f_{j}+v_{j,i'}$，$\square$

通用解法

一般的，我们使用单调队列+二分查找的方式对决策进行维护

例：[NOI2009] 诗人小G

小 G 是一个出色的诗人，经常作诗自娱自乐。但是，他一直被一件事情所困扰，那就是诗的排版问题。

一首诗包含了若干个句子，对于一些连续的短句，可以将它们用空格隔开并放在一行中，注意一行中可以放的句子数目是没有限制的。小 G 给每首诗定义了一个行标准长度（行的长度为一行中符号的总个数），他希望排版后每行的长度都和行标准长度相差不远。显然排版时，不应改变原有的句子顺序，并且小 G 不允许把一个句子分在两行或者更多的行内。在满足上面两个条件的情况下，小 G 对于排版中的每行定义了一个不协调度, 为这行的实际长度与行标准长度差值绝对值的 $P$ 次方，而一个排版的不协调度为所有行不协调度的总和。

小 G 最近又作了几首诗，现在请你对这首诗进行排版，使得排版后的诗尽量协调（即不协调度尽量小），并把排版的结果告诉他。

诗句的数量 $n\leq 10^5$。

设 $f_{i}$ 表示在第 $i$ 个诗句换行，前 $i$ 句诗的最小不协调度，记每句诗的长度为 $a_i$，前 $i$ 首诗的长度和为 $s_i$，则有转移

\[f_i=\min_{j=1}^{i-1}\{f_i+|s_i-s_j+i-j-L-1|^{P}\} \]

想要优化就只能往决策单调性上想了。打个表发现 $w(j,i)=|s_i-s_j+i-j-L-1|^P$ 满足四边形不等式，于是考虑证明。

$\text{proof.}$

凸优化

推荐阅读：凸优化常见技巧做题笔记-KingPowers 以及文中的推荐文章。

wqs 二分

我们要解决的问题一般都是类似于区间分拆问题，其 2D-1D 递推式一般都类似：

\[f_{k,i}=\operatorname{opt}\{f_{k-1,j}+w(j+1,i)\} \]
其中 $w(i,j)$ 满足四边形不等式。设 $g(k):=f(n,k)$，那么有 $g(k)$ 是凸函数。

$\text{proof.}$

尝试证明 $g(k-1)+g(k+1)\geq 2g(k)$。考虑一个长度为 $k-1$ 的分拆 $[a_1,d_1],\dots,[a_{k-1},d_{k-1}]$ 与一个长度为 $k+1$ 的分拆 $[b_1,c_1],\dots,[b_{k+1},c_{k+1}]$。然后想着怎么去构造出两个长度为 $k$ 的分拆，也就是把上面两个融合在一起，于是想到找一个最小的 $j$ 满足 $c_{j+1}\leq d_j$，由 $d_{k-1}=n$ 可知其必然存在，随后根据其最小性，我们知道$a_j<b_{j+1}\leq c_{j+1}\leq d_j$，于是从 $j$ 把序列拆开，把两端末尾交换得到

\[[a_1,d_1],\dots, [a_{j-1},d_{j-1}],[a_j,c_{j+1}],[b_{j+2},c_{j+2}],\dots,[b_{k+1},c_{k+1}] \iff [b_1,c_1],\dots ,[b_{j+1},d_j],[a_{j+1},d_{j+1}],\dots,[a_{k-1},d_{k-1}] \]
于是 $2g(k)$ 小于等于上面的区间的权值加一块，由四边形不等式可知 $2g(k)\leq g(k-1)+g(k+1)$。

$\text{Q.E.D.}$

以上文字是我之前在 cnblogs 上写的，自以为掌握了一个数学模型能够不用脑子利用 wqs 二分切题的方法，可这样的数学模型真的足够普适吗？显然不！也许王钦石在发明这个方法的时候确实是从 dp 问题中归纳出来的数学模型，但经过后人的推广之后，wqs 二分的应用范围已经不仅仅局限于 dp。更普适的模型如下：

对于定义在自然数域上、值域为正整数的凸包 $f(x)$，要求在某个特定点上的函数值，而我么难以直接求 $f(x)$，但是容易求出 $f(0)$。我们利用函数的凸性，也就是 $\delta f(x)$ 单调的性质二分斜率，考虑这个斜率 $k$的直线切凸包的时候，所对应的切点满足的就是 $f(x)-xk$ 最小，实际应用中相当于是对每个点值强制加上一个 $-k$ 的权值然后计算 $f'(0)$，当然这对于讨论数学模型中没有意义。

那我之前写的真的就一无是处吗？显然不！把那一大段贴上是因为这个二级结论非常常用，能方便我们做题。

[国家集训队] Tree I

给定一个无向带权连通图，每条边是黑色或白色，求一棵最小权的恰有 $k$ 条白边的生成树，$|V|\leq 5\times 10^4,|E|\leq 10^5$。

设 $f(x)$ 表示恰有 $x$ 条白边的生成树的最小权，打表发现 $f(x)$ 是个凸包，二分斜率 $p$，给每白边的权值减 $p$ 跑 MST 就行。

Luogu P4983 忘情

算得上板子中的板子了，直接搬运我之前写的。

设 $f_i$ 表示在 $i$ 处分段，前 $i$ 段的最小值，记 $s_i=\sum_{j=1}^ia_i$，有转移

\[f_{i}=\min_{j=1}^{i-1}\{f_j+(s_i-s_{j})^2+c\} \\ = \min\{f_{j}+s_i^2-2s_is_j+s_j^2+c\} \\ = \min\{-2s_j\times s_i +s_j^2+f_j\}+s_i^2+c \]

如果对于某个 $c$，求出来的答案正好分成了 $m$ 段，那么求出来的答案减去 $ck$ 就是我们要求的。显然地，$c$ 越大，段数越小，所以我们二分 $c$，获得一个段数恰好为 $m$ 的答案。如果对于 $c=x$，段数小于 $m$，对于 $c=x+1$，段数大于 $m$，那么取 $c=x+1$ 时也存在分段数为 $k$ 的做法，只需把答案减去 $(x+1)m$。这样我们就得到了 $O(n\log C)$ 的做法，很优！

Luogu P5633 最小度限制生成树

给你一个有 $n$ 个节点，$m$ 条边的带权无向图，你需要求得一个生成树，使边权总和最小，且满足编号为 $s$ 的节点正好连了 $k$ 条边，$1\leq s\leq n \leq 5\times 10^4$，$1\leq m \leq 5\times 10^5$，$1\leq k \le 100$，$0\leq w\leq 3\times 10^4$。

设 $f(x)$ 表示 $s$ 连了 $x$ 条边的最小生成树权值和，尝试证明 $f(x)$ 是凸的。

$\text{proof.}$

显然对 $|T|=1,2$ 的时候成立。

假设对于 $|T|\leq n$ 均成立。设当前的树 $|T|=n$，最小边是 $e$，删去 $e$ 后两棵树是 $T_1,T_2$，发现 $f_T(k)=\min(f_{T_1}(k_1)+f_{T_2}(k_2))$ 是 $(\min,+)$ 是两个函数的闵可夫斯基和，由归纳假设可知对所有 $T$ 函数都是凸的，$\square$

于是二分斜率，给 $s$ 连的边权减去 $mid$ 跑 MST 就行。

Minkowski 和

定义是对于两个点集 $A,B$，它们的闵可夫斯基和为点集 $C=\{a+b|a\in A, b\in B\}$。

这对于普通的点集来说并没有什么值得研究的，但是对于两个凸包来说就有的搞头了。盗一下经典图。

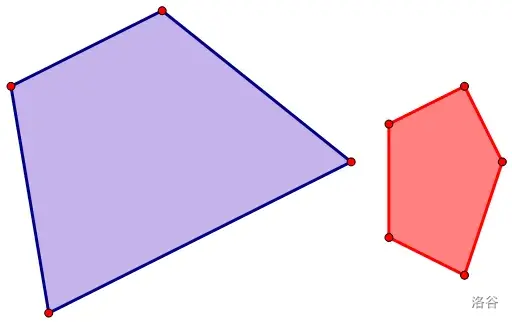
minkowski

对上面两个凸包做 Minkowski 和，得到新的点集：

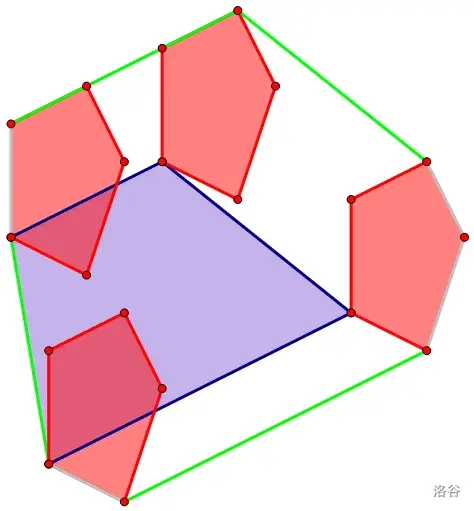
minkowski-sum

发现把边看成向量的话新凸包的边就是把原来两个凸包的边按照斜率排序之后顺次拼接形成的。这非常有用，假设有 $f,g$ 两个凸壳我们可以 $O(|f|+|g|)$ 合并为新的凸壳，更具体的，对于两个下凸壳 $f,g$ 的 $(\min,+)$ 卷积，也就是 $h_{k}=\min_{j+k}(f_j+g_k)$，因为 $f,g$ 都是下凸壳，所以 $h$ 就相当于 $f,g$ 上点相加后对每个 $x$ 取最小的点，发现这就是闵和，也就是说对下凸的数组做 $(\min,+)$ 卷积是线性的，对于上凸的函数做 $(\max,+)$ 卷积同理。代码辅助理解。

inline vector<int> merge(vector<int> a, vector<int> b)
{
 vector<int> c;
 c.pb(a[0] + b[0]);
 int l = 1, r = 1;
 while (l < a.size() && r < a.size())
 {
  if (a[l] - a[l - 1] < b[r] - b[r - 1]) c.pb(a[l] - a[l - 1]), ++l;
  else c.pb(b[r] - b[r - 1]), ++r;
 }
 while (l < a.size()) c.pb(a[l] - a[l - 1]), ++l;
 while (r < b.size()) c.pb(b[r] - b[r - 1]), ++r;
 fo(i, 0, c.size() - 1) c[i] += c[i - 1];
 return c;
}

2020 ICPC Shenyang R L.Forged in the Barrens

给定数列 $\{a_n\}$，你需要将它分为 $k$ 部分，每部分的价值定义为极差，对所有 $k\in [1\dots n]\cap \mathbb{Z}$，求最大价值和。$n\leq 10^5,a_i\leq 10^9$。

套路化的设 $f_{i,j}$ 表示前 $i$ 个数分了 $j$ 段的最大价值和，直接枚举前面的位置是 $O(n^3)$ 并且没有特殊性质，难以优化到一个可过的做法，考虑一个区间的极差等价于任选两数相减的最大值，于是设 $f_{i,j,0/1/2}$ 表示前 $i$ 个数选了 $j$ 段，最后一段对答案有负贡献/零贡献/正贡献时的最大价值，这样就能做到 $O(1)$ 转移从而做到 $O(n^2)$，似乎到这里就卡住了，不过打出表来发现 $f_n$ 关于 $k$ 是上凸的。

然后有一个技巧就是把序列上的 dp 当做区间 dp 去做，设 $f_{l,r,0/1/2,0/1/2,k}$ 表示区间 $[l\dots r]$ 分了 $k$ 段，其中左端点、右端点对答案的贡献分别是负贡献/零贡献/正贡献，转移时考虑任取一个断点 $mid$，有

\[f_{l,r,ol,or,k}=\max\begin{cases} \max(f_{l,mid,ol,or,k},f_{mid+1,r,ol,or,k}) \\ \max\limits_{x+y=k}(f_{l,mid,ol,1,x}+f_{mid+1,r,1,or,x})\\ \max\limits_{x+y=k-1}(f_{l,mid,ol,0,x}+f_{mid+1,r,2,y})\\ \max\limits_{x+y=k-1}(f_{l,mid,ol,2,x}+f_{mid+1,r,0,y}) \end{cases} \]

$mid$ 取在中点的时候就得到了类似线段树的分治结构，时间复杂度 $O(n\log n)$。

2022 ICPC Nanjing R H.Factories Once More

$n$ 个点的树，边带权，树上选 $k$ 个点使两两距离和最大，$1\leq k\leq n\leq 2\times 10^5$，边权在 $[1,10^9]$ 中间。

暴力树背包是设 $f_{u,i}$ 表示点 $u$ 的子树里面选了 $i$ 个点的答案，考虑合并子树，$f_{u,x}=\max_{i+j=x}\{f_{u,i}+f_{v,j}+w(u,v)\cdot j\cdot (k-j)\}$，发现 $j(k-j)$ 是开口向下的二次函数，每次合并做的是 $(\max,+)$ 卷积，可证背包是上凸的，于是每次我们要做的就是两个差分数组相加，考虑 $+w(u,v)j(k-j)$ 对差分的影响是怎么样的，写式子发现是 $w(k-2j+1)$ 是个一次函数，考虑维护一个本身有序的数据结构然后 dsu on tree 地合并，也就是说维护平衡树，对子树打一个一次函数的 tag 就行了。发现 $f_{u,0}=0$ 可以不维护，时间复杂度 $O(n\log^2n)$。

slope trick

什么是 slope trick？如图：

slope-trick

upd.2025/11/1 已经被推平了。

用于优化呈分段一次函数状的 dp，当然也要求是凸的，也就是说 $g(x)=\Delta f(x)$ 是单调的，尝试维护 $g(x)$ 变化的拐点，维护一个集合，每扔进一个点意味着这个点往后斜率变化了 1，扔进几次斜率就变化了多少，这要求斜率变化不是很大。一般考虑每一步 dp 转移对斜率的影响。后面称“斜率为 $k$ 的拐点”为后面直线斜率为 $k$ 的点。

dp 的设计并非该算法的重点（虽然对于题目至关重要），而凸性证明在闵和的基础上已经有了充足的技术支撑，因此学 slope trick 重点是把转移对差分数组的影响想明白。

CF713C Sonya and Problem Without a Legend 加两个 0

给定 $\{a_n\}$，每次可以选一个数加一或减一使序列单增，求最小次数，$n\leq 3\times 10^5,1\leq a_i\leq 10^9$。

$a_i\leftarrow a_i-i$，问题转化成单调不减，这样改一个数只可能改成之前出现过的一个数。设 $dp_{i,j}$ 表示 $a_i\leftarrow j$ 的最小次数，有转移 $dp_{i,j}=\min_{k=1}^j \{dp_{i-1,k}\} + |a_i-j|$，这样直接做就是 $O(n^2)$ 的。设 $f_{i}(x)=dp_{i,x}$，归纳可证 $f(x)$ 是凸的，考虑维护拐点，dp 过程相当于前缀 min 与加 $|a_i-x|$，对于前缀 min 操作抹掉斜率大于 0 的部分就行了，对于加 $|a_i-x|$，找到斜率为 0 的拐点 $p$，如果 $a_i\geq p$ 那么直接加入 $a_i$，否则 $a_i$ 位置斜率变化量为 2，后面的会被抹平，直接扔掉就行了。

CF372C Watching Fireworks is Fun 加七个 0

$n$ 各区域，$m$ 个烟花要放，给定地点 $a_i$ 与时间 $t_i$，如果你在 $x$ 会获得 $b_i-|a_i-x|$ 的开心值，每个单位时间最多移动 $d$，求通过移动最大开心值，$n\leq 10^9,m\leq 2\times 10^5,a_i,b_i,t_i\leq 10^9$， $t_i$ 单增。

相当于 $\sum |a_i-x|$ 最小值，暴力 dp 设 $dp_{i,x}$ 表示第 $i$ 个烟花在 $x$ 的最大开心值，转移是滑动窗口，$dp_{i,x}=|a_i-x|+\min_{x-d\Delta t\leq y\leq x+d\Delta t}dp_{i-1,y}$ 设 $f_i(x)=dp_{i,x}$ 于是 $f(x)$ 显然是凸的考虑维护拐点，$\min_{x-d\Delta t\leq y\leq x+d\Delta t}dp_{i-1,y}$ 相当于对于小于等于 0 的拐点左移 $d$，大于 0 的拐点右移 $d$，$+|a_i-x|$ 考虑最小值区间 $[l,r]$ 如果 $a_i\in [l,r]$ 相当于 $a_i$ 位置上加两个拐点，$a_i<l$ 相当于 $a_i$ 上的斜率 -2 并成为新的 0 斜率点，$a_i>r$ 与上面的对称，然后开两个堆维护小于等于 0 和大于 0 的拐点，平移直接打标记，最小值实时维护即可。

[OOI 2025] The arithmetic exercise

给定 $\{a_n\}$，初始时全为 0，同时 $m$ 个数 $x_1,x_2,\dots,x_m$，对于 $1\leq i\leq m$ 选择某个下标 $j_i$，使 $a_{j_i}\leftarrow x-a_{j_i}$，求操作完后 $\sum a_i$ 的最大可能。$n,m\leq 300000,-10^9\leq x_i\leq 10^9$。

正着做会导致前面定了符号的 $x_i$ 被取反这很不好维护，反着做就没有这样的问题所以把序列取反后缀改前缀，假设符号序列为 $\{k_n\}$，那么这个序列合法当且仅当 $\forall i\in [1,n],0\leq\sum_{j=1}^ik_i\leq n$，于是枚举这个值，设 $f_{i,j}$ 表示考虑到 $x_i$，$k_i$ 的前缀和为 $j$ 的答案，有转移 $dp_{i,j}=\max\{dp_{i-1,j-1}+x_i,dp_{i-1,j+1}-x_i\}$ 发现这相当于关于 $j$ 的函数 $dp_{i,j}$ 和 ${-x_i,x_i}$ 做 $(\max,+)$ 卷积（钦定 $-x_i$ 的下标为 -1，$x_i$ 下标是 1），考虑归纳证明 $f_i(j)=dp_{i,j}$ 的凸性。对于 $f_0$ 凸性显然，对于 $i-1\rightarrow i$ 的转移由 Minkowski 和经典结论可知如果 $f_{i-1}$ 是凸的那么 $f_i$ 也是凸的，由归纳原理凸性得证。用闵和的方式维护差分的形式是不可行的，考虑 slope-trick 地维护拐点，考虑一次转移 $i-1\rightarrow i$ 的影响，发现这种两边向中间的平移不好维护，考虑先把答案减去 $\sum x_i$，这样先把 $f_{i-1}$ 平移，然后 $dp_{i,j}=\max\{dp_{i,j},dp_{i-1,j-2}+2x_i\}$，又发现 $dp_{i,j}$ 有值当且仅当 $i,j$ 奇偶性相同，于是 $j-2\rightarrow j$ 可以改成 $j-1\rightarrow j$，改一下范围即可，弄明白这些就可以 multiset 维护拐点做了。

动态 dp

得得得得得得得得得得得得得得得得得得得得得得得得得得得得得得p（bushi

就是基于广义矩阵乘法的带修 dp。

广义矩阵乘法

设 $\oplus$ 和 $\otimes$ 是两种运算，定义两个矩阵 $A,B$ 的广义矩阵积为

\[c_{i,j}=\bigoplus_{k=1}^l a_{i,k}\otimes b_{k,j} \]

其中 $A$ 是 $n\times l$ 的矩阵，$B$ 是 $l\times m$ 的矩阵，$C$ 也就是 $n\times m$ 的矩阵。

定理1 如果 $\oplus,\otimes$ 都有结合律，并且 $\oplus$ 对 $\otimes$ 有分配律，那这个广义矩乘也有结合律。

定理2 仍然是上面的条件，有 $(A\times B)\oplus(A\times C)=A\times(B\oplus C)$。

最常见的有 $\oplus=\max/\min,\otimes=+$，结合律和分配律显然。

还有 $\oplus=\operatorname{xor},\otimes=\operatorname{and}$，对于 01 的情况是有分配律的，因此对任意位都有分配律。

序列上 ddp

一般是通过数据结构维护矩阵乘法来进行矩阵复合的操作。

CF618E Robot Arm

机械臂由 $n$ 节组成，每节坐标初始为 $(i,0)$ 和 $(i+1,0)$，每次操作将其中一个机械臂伸长 $l$ 或者旋转 $\alpha$，每次操作后输出最后一个点的位置。

每一节可以用两维上的平移表示，平移操作是容易线段树维护的，对于旋转操作发现每次旋转会让后面的跟着转，由于旋转有交换律所以可以差分旋转，也可以从后往前线性变换这样前面的旋转就作用于后面的了。

单点修改区间最大子段和。

多次询问，单点修改，求区间最大子段和。

$dp(i)$ 表示右端点为 $i$ 的最大子段和，$ans(i)$ 表示前 $i$ 个的答案。有

\[dp(i)=\max(dp(i-1)+a_i,a+i) \]

\[ans(i)=\max(dp(i),ans(i-1)) \]

矩阵写出来就好了。还是线段树维护。

树上 ddp

Luogu P4719【模板】动态 DP

多次修改，多次查询树上最大独立集。

静态的 dp 是经典的树上最大独立集问题。

一条链上或者说序列的话我们有序列上 ddp。$dp(i,0/1)$ 表示考虑到 1 到 $i$，$i$ 选不选的答案。矩阵就不列了，线段树维护即可。

一个用 ds 维护的东西扔到了树上，第一反应应该都是树剖。树剖其实是把树拆成了重链和轻边，我们这里考虑轻边。naive 的想法是直接给每个 $v$ 的转移矩阵合并起来，但是我不会合并转移矩阵，考虑把轻儿子一块处理了，设 $g(u,0/1)$ 表示不选 $u$ 轻儿子随便的方案，$g(u,1)$ 表示选 $u$ 的方案，然后再算重儿子就有转移矩阵

\[\begin{bmatrix} g_{u,0} & g_{u,0}\\ g_{u,1} & -\infty\\ \end{bmatrix} \begin{bmatrix} f_{v,0}\\ f_{v,1}\\ \end{bmatrix} = \begin{bmatrix} f_{u,0}\\ f_{u,1}\\ \end{bmatrix} \]

然后就好做了。放一个代码，顺便推销板子库。

状态压缩相关

可以看做 command_block 的博客的誊抄。

从一道题讲起

这道题目是 AT_typical90_w，你别想从洛谷找到它。

一个 $H\times W$ 的网格，其中有的点是白点，有的点是黑点。我们要在白点上放若干个王，满足王不见王，求方案数。

王不见王的定义就是说一个王和它八联通的点里面没有第二个王。

写“王不见王”定义时我的大脑：

牛顿高斯比我提前出生，是笨鸟先飞还是避我锋芒？？？！！！

秦王嬴政比我早生千年，是惧我三分还是王不见王？？？！！！

（逃

naive 状态压缩做法

我们一行行填。$dp(i,S)$ 表示第 $i$ 行放国王的方案是 $S$ 的方案数。枚举上一行的集合 $T$，判断 $T$ 和 $S$ 是否合法可以用位运算做到 $O(1)$，时间复杂度 $O(n4^m)$。输麻了。

枚举子集的优化。

发现上一行确定了哪些点不能填，也就是说能填的集合是一个确定的集合的子集。我们通过 for (int T = S; T; T = (T - 1) & S) 来枚举子集。这个总量是 $3^m$ 的，时间复杂度就降成了 $O(n3^m)$ 的。这样能解决大部分这一类的问题！

进一步压缩规模。

对于一行来说，我们发现实际情况下可行的集合远小于 $3^m$。我们数一下。设 $f(i,0/1)$ 表示考虑到前 $i$ 位，最后一位是 $0/1$ 的可行的集合数。不考虑强制的不能填的位置，那有递推式

\[f(i+1,1)=f(i,0),f(i+1,0)=f(i,0)+f(i,1) \]

代换一下发现这玩意构成了斐波那契数列！所以我们的可行的集合数是 $fib(m)$ 的，这远小于 $3^m$，预处理可行的集合数，总复杂度就是 $O(n(fib(m))^2)\leq O(n\phi^2)$。

轮廓线。

我们发现填表的方式相当于从上到下/从左到右填，所以说填好的轮廓线大概就是 _|$^{-}$ 这个样子，维护拐点即可维护轮廓线位置，轮廓线上的信息可以状态压缩维护。

设 $dp(i,j,S)$ 表示拐点在 $(i,j)$，轮廓线上的信息为 $S$ 的方案数，我们只用考虑 $(i,j)$ 位置上的填法和轮廓线给他的限制即可。时间复杂度 $O(nm2^m)$。很优但是无法通过。

拼好优化，拿下这道题！

我们在轮廓线 dp 之前维护可行的 $S$，可知 $S$ 的规模仍然是 $O(fib(m))$ 的，于是我们就有了 $O(nmfib(m)+2^m)$ 的理论复杂度的做法！！！可以通过！！！

对每个过程我都写了代码，可以在板子库里看到它们。

lhc0707