支持向量机SVM

一、概念
支持向量机（SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面，可以将问题化为一个求解凸二次规划的问题。与逻辑回归和神经网络相比，支持向量机，在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式。
具体来说就是在线性可分时，在原空间寻找两类样本的最优分类超平面。在线性不可分时，加入松弛变量并通过使用非线性映射将低维度输入空间的样本映射到高维度空间使其变为线性可分，这样就可以在该特征空间中寻找最优分类超平面。
SVM使用准则： 为特征数， 为训练样本数。
如果相较于而言，要大许多，即训练集数据量不够支持我们训练一个复杂的非线性模型，我们选用逻辑回归模型或者不带核函数的支持向量机。
如果较小，而且大小中等，例如在 1-1000 之间，而在10-10000之间，使用高斯核函数的支持向量机。
如果较小，而较大，例如在1-1000之间，而𝑚大于50000，则使用支持向量机会非常慢，解决方案是创造、增加更多的特征，然后使用逻辑回归或不带核函数的支持向量机。

二、间隔
只考虑二分类问题，假设有n个训练点xi，每个训练点有一个指标yi。训练集即为：T={(x1,y1),(x2,y2),....(xn,yn)} 其中xi 为输入变量，其分量称为特征或属性。yi是输出指标。问题是给定新的输入x，如何推断它的输出y是1还是-1。
处理方法是找到一个函数，然后定义下面的决策函数实现输出。
f(x)=sgn(g(x))
其中sgn(z)是符号函数，也就是当z>=0时取值+1，否则取值-1。确定g的算法称为分类机。如果g(x)=WtX+b ，则确定w和b的算法称为线性分类机。

三、求解
假设两类数据可以被H分离，垂直于法向量W，移动直到碰到某个训练点，可以得到两个超平面H1和H2，两个平面称为支撑超平面，它们分别支撑两类数据。而位于H1和H2正中间的超平面是分离这两类数据最好的选择。

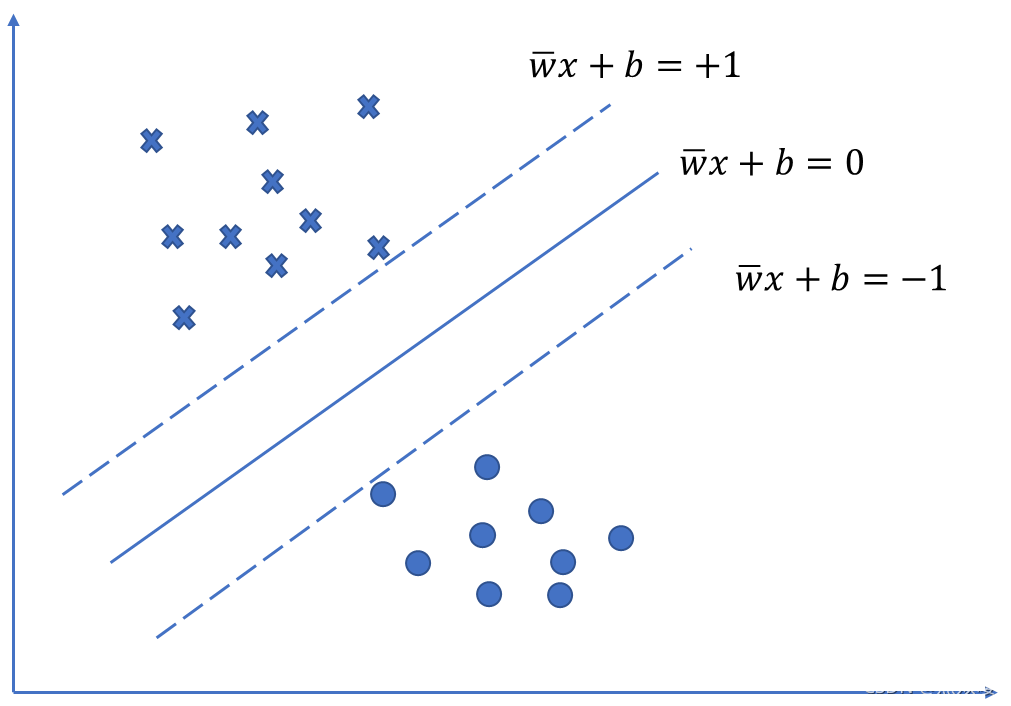
法向量W有很多中选择，超平面H1和H2之间的距离称为间隔，这个间隔是w的函数，目的就是寻找这样的w使得间隔达到最大。

SVM中，分隔超平面是一个能够将正负样本恰好隔开的超平面，并且使得正样本在分隔超平面“上方”，负样本在分隔超平面”下方“。这就意味着，分隔超平面中的需要满足以下条件：

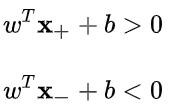
其中x+为正样本点，x-为负样本点，而正负样本对应的标记值为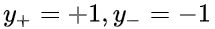
，所以这两个条件可以改写成下面两个式子：

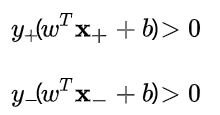
于是，对于线性可分的样本集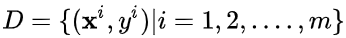：其中
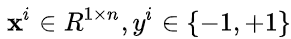
令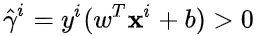
，我们可以得到更加紧凑的表达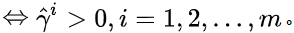："分类正确"
在SVM中，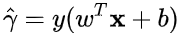
被称为样本点到超平面的函数间隔。

因此，我们可以得出结论，对于给定的线性可分的样本集合，必然存在分隔超平面可以将正负样本分开，该分类正确的超平面需要满足的条件为：样本点到超平面的函数间隔大于零。
在数学上，我们可以得到以下式子等效：

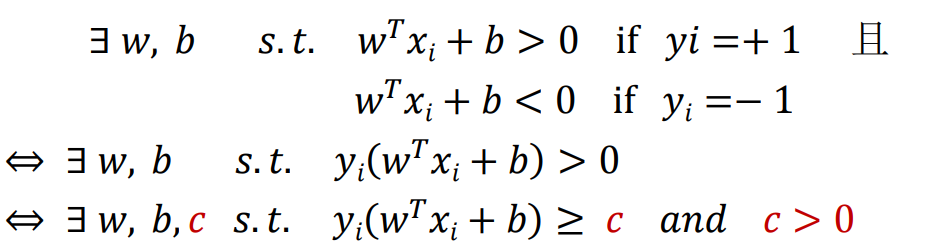
所以，为了方便后续的计算，简化方程为：
[](https://img2023.cnblogs.com/blog/2193951/202301/2193951-20230101014303008-1229633880.png

令X+和 X- 位于决策边界上，标签分别为正、负的两个样本，考虑 到分类线的距离为: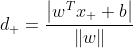

因此，分类间隔为：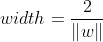
最大化间隔也就是寻找参数w和 b, 使得width最大，即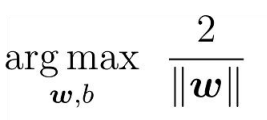：,最后得出了求解最大间隔超平面的最终表达式

四、实验
1.准备数据
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris() # 加载鸢尾花数据集
X = iris.data # 样本特征
y = iris.target # 样本标签
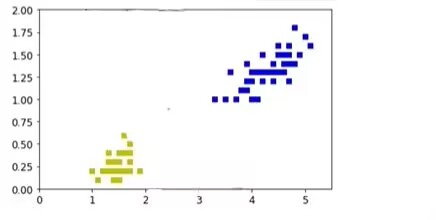
X = X[y<2,:2] # 选择前两种花，为了可视化，只选择前两个特征
y = y[y<2]
plt.plot(X[:,0][y1],X[:,1][y1],'bs')
plt.plot(X[:,0][y0],X[:,1][y0],'ys')

plt.show()

from sklearn.svm import SVC
from sklearn import datasets

iris = datasets.load_iris()
X =iris['data'][:,(2,3)]
y=iris['target']

setosa_or_versicolor = (y0)|(y1)
X =X[setosa_or_versicolor]
y= y[setosa_or_versicolor]

svm_clf = SVC(kernel='linear',C=float('inf'))
svm_clf.fit(X,y)

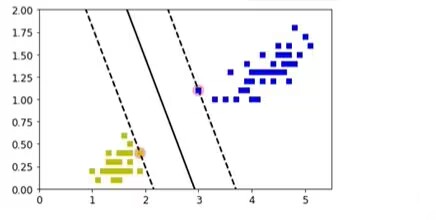
2.进行一般模型的训练

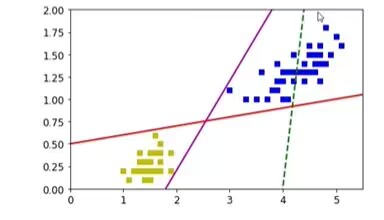
一般的模型

x0= np.linspace(0,5.5,200)
pred_1= 5x0 -20
pred_2= x0-1.8
pred_3= 0.1x0+0.5

def plot_svc_decision_boundary(svm_clf,xmin,xmax,sv=True):
w=svm_clf.coef_[0]
b=svm_clf.intercept_[0]
x0=np.linspace(xmin,xmax,200)
decision_boundary=-w[0]/w[1]*x0-b/w[1]
margin=1/w[1]
gutter_up=plot_svc_decision_boundary+margin
gutter_down=plot_svc_decision_boundary-margin
if sv:
svs =svm_clf.support_vectors_
plt.scatter(svs[:,0],svs[:,1],s=180,facecolors='#FFAAAA')
plt.plot(x0,plot_svc_decision_boundary,'k--',linewidth=2)
plt.plot(x0,gutter_up,'k--',linewidth=2)
plt.plot(x0,gutter_down,'k--',linewidth=2)
plt.figure(figsize=(14,4))
plt.subplot(121)
plt.plot(x0,pred_1,'g--',linewidth=2)
plt.plot(x0,pred_2,'m-',linewidth=2)
plt.plot(x0,pred_3,'r-',linewidth=2)
plt.plot(X[:,0][y1],X[:,1][y1],'bs')
plt.plot(X[:,0][y0],X[:,1][y0],'ys')
plt.axis([0,5.5,0,2])

plt.subplot(122)
plot_svc_decision_boundary(svm_clf,0,5.5)
plt.plot(X[:,0][y1],X[:,1][y1],'bs')
plt.plot(X[:,0][y0],X[:,1][y0],'ys')
plt.axis([0,5.5,0,2])

五、实验总结
svm的优缺点
优点：
支持向量机算法可以解决小样本情况下的机器学习问题，简化了通常的分类和回归等问题。
由于采用核函数方法克服了维数灾难和非线性可分的问题，所以向高维空间映射时没有增加计算的复杂性。换句话说，由于支持向量计算法的最终决策函数只由少数的支持向量所确定，所以计算的复杂性取决于支持向量的数目，而不是样本空间的维数。
支持向量机算法利用松弛变量可以允许一些点到分类平面的距离不满足原先要求，从而避免这些点对模型学习的影响。
缺点：
支持向量机算法对大规模训练样本难以实施。这是因为支持向量机算法借助二次规划求解支持向量，这其中会涉及m阶矩阵的计算，所以矩阵阶数很大时将耗费大量的机器内存和运算时间。
经典的支持向量机算法只给出了二分类的算法，而在数据挖掘的实际应用中，一般要解决多分类问题，但支持向量机对于多分类问题解决效果并不理想。
SVM算法效果与核函数的选择关系很大，往往需要尝试多种核函数，即使选择了效果比较好的高斯核函数，也要调参选择恰当的参数。另一方面就是现在常用的SVM理论都是使用固定惩罚系数C，但正负样本的两种错误造成的损失是不一样的。