题2

8.6

P1377 [TJOI2011] 树的序

题解：

1. 其实就是把二叉搜索树建出来然后先序遍历即可，因为发现，先序遍历的过程其实就相当于插入节点
2. 考虑如何建二叉搜索树，又能发现，题目里的建树保证了权值满足二叉搜索树，下标满足堆，那不得不想到笛卡尔树了，但是笛卡尔树是下标满足二叉搜索树，权值满足堆，所以可以直接把权值和下标互换，然后建笛卡尔树即可。所以笛卡尔树的作用是建树

code

P4036 [JSOI2008] 火星人

注意：不论什么操作都要\(splay\)；如果要把\(x\)转到根或\(goal\)下面，首先要判断\(x\)是否大于\(n\)

8.7

P4139 上帝与集合的正确用法

题目简述：\(x=2^{2^{2^{\dots}}}\),可以证明\(x\)在大到一定值的时候\(\mod p\)的值会变成一个定值，要求求出这个定值\(\mod p\)。

题解：题意可以转化成\(x\equiv 2^x(\mod p)\),求\(x\mod p\)，那么由欧拉定理（不会证），\(x\equiv 2^{x\mod\varphi(p)+\varphi(p)}(\mod p)\),那么我们发现只需要求出\(x\mod\varphi(p)\)即可，那么实际上就相当于\(p\gets\varphi(p)\),然后递归求就行，最终\(\varphi(p)\)会变成\(1\)，这时直接返回\(0\)，即可

8.8

P5410 【模板】扩展 KMP/exKMP（Z 函数）

考虑如何求\(z\)数组，首先维护一个已求出的\(z_i\)，使得\(i+z_i-1\)最大，然后如果当前求的\(j\)在\([i,i+z_i-1]\)之间，那么考虑利用\(z_i\)，即找到\(z_{i+z_i-1-j+1}\)，利用该\(z\)函数求出\(z_j\)，我们更具体一点说：令\(l=i,r=i+z_i-1\)，当前处理的位置为\(j\)，如果\(l\le j\le r\)，那么因为\(s[1,r-l+1]=s[l,r]\),所以，可以找到一个\(j\)的对应点\(t\)，即\(t=r-j+1\)，如果\(t+z_t-1<r-l+1\),那么说明后面已经不能在进行匹配了，所以\(z_j=z_t\)，反之，如果\(t+z_t-1\ge r-l+1\)，说明后面可能还有更多相同的数，所以应该把\(z_j=r-j+1\)，然后暴力拓展即可。如果\(j>r\)，那么暴力找就行。
该题的第二个问题，实际上就是把\(a\)拼接到\(b\)后面，然后求\(z\)函数即可

P7114 [NOIP2020] 字符串匹配

题解：直接枚举\(AB\)的长度，然后怎么判断是否是循环，且循环了多少次呢？其实就是\(z[i+1]/i\)，\(i\)是\(AB\)的长度，\(z\)数组是\(ex_kmp\)里的（可以画图理解一下）。然后呢，如何求一个子串中出现次数为奇数次的字符数量，因为需要的子串都是前后缀，所以可以状压一个前后缀数组\(pre,suf\)，例如，\(pre[i]\)是\(i\)前缀中每个字符出出现的奇偶性，这样，想要查询数量，只要输出cpp __builtin_popcount(pre[i])即可。这些解决了，考虑如何统计答案，发现，如果\(AB\)的长度确定，那么\(C\)也基本是确定的，首先先找到最小长度的\(C\)，然后在\(C\)前加\(AB\)即可，考虑如何满足\(f\)的性质，首先能发现\(C\)加上\(AB\)的\(f\)值至多会有两个，因为是奇偶性，所以只需要看\(f(C)\)和\(f(C+AB)\)。然后考虑如何分\(AB\)，其实就是找到\(s[1，len(AB)-1]\)中前缀\(f\)值$\le f(C) or f(C+AB) $的个数即可，那么如何找呢，用树状数组就行。

code

8.9

P3809 【模板】后缀排序

最需要理解的地方就是排序的时候了,直接上代码

for(int k = 1; k <= n; k <<= 1) {
        for(int i = 1; i <= n; i ++) c[i] = 0;
        for(int i = 1; i <= n; i ++) c[x[i]] ++; 
        for(int i = 1; i <= n; i ++) c[i] += c[i - 1];
        num = 0;
        for(int i = n - k + 1; i <= n; i ++) {
            y[++ num] = i;
        }
        for(int i = 1; i <= n; i ++) {
            if(sa[i] > k) {
                y[++ num] = sa[i] - k; 
            }
        }
        for(int i = n; i >= 1; i --) {
            sa[c[x[y[i]]] --] = y[i];
            y[i] = 0;
        }
        num = 1;
        swap(x, y);
        x[sa[1]] = 1;
        for(int i = 2; i <= n; i ++) {
            x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++ num;
        }
        if(num == n) return;
    }

其中\(x_i\)表示以\(i\)为开始的后缀的排名，\(y_i\)表示的是按照第二关键字排序的后排名为\(i\)的后缀编号，\(c\)就是存放第一关键字的桶，\(sa[c[x[y[i]]] --]=y[i]\)这个是基于基数排序的过程，参考OI wiki
然后那么看最后的这个循环，\(x[sa[i]]\)理应是\(i\)，但是可能有相同的，也就是第一关键字和第二关键字都相同的，这时两个的排名就就是相同的。

P1447 [NOI2010] 能量采集

题目：有一个\(n\times m\)的点阵，每个点上有一棵植物，需要将这些植物全部收集，收集的代价为\((x,y)\)点到\((0,0)\)点的连线上有多少棵植物（不包含自己）乘\(2\)，加\(1\)，例如，收集\((4,2)\)的植物所需要的花费为\(2\times 2+1\)

转化：发现连线上的植物数量为\(\gcd(i,j)-1\)，那么答案就是:

\[\sum_{i=1}^{n}\sum_{j=1}^{m}(2\times(\gcd(i, j)-1))+1 \]

多余的常数是无用的，所以可以提出来，所以实际上只需要求出\(\sum_{i=1}^{n}\sum_{j=1}^{m}\gcd(i,j)\)即可,式子又可以转化成\(\sum_{i=1}^{n}\sum_{j=1}^{m}id(\gcd(i,j))\),根据\(\varphi*i=id\),然后就卷积嘛，最终的形式为：

\[\sum_{d=1}^{n}\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor\varphi(d) \]

然后问题就转化成了线性求\(\varphi(d)\)
因为\(\mu(d)\)是积性函数，因为积性函数大多都可以用欧拉筛或埃式筛求出，那么下面用欧拉筛做例子：

for(int i = 2; i <= n; i ++) {
    if(!p[i]) {
        l[++ l[0]] = i;
        phi[i] = i -  1;
    }
    for(int j = 1; j <= l[0] && i * l[j] <= n; j ++) {
        p[i * l[j]] = 1;
        if(i % l[j] == 0) {
            phi[i * l[j]] = phi[i] * l[j];
            break;
        }else {
            phi[i * l[j]] = phi[i] * (l[j] - 1);
        }
    }
}

就是，先将\(n\)唯一分解成\(\prod_{i}^{k}p_i^{c_i}\),\(\varphi(n)=n\prod_i^k(1-\frac{1}{p_i})=\prod_i^k p_i^{c_i-1}\prod(p_i-1)\),也就是说，筛到他的最小质因子的时候乘\(p_i-1\)，否则乘\(p_i\)。

推广一下，如果线性求\(\mu\)，那么如果当前\(i\equiv 0\mod l[j]\),则\(i*l[j]\)中\(l[j]\)的次幂大于等于\(2\)，所以含平方因子，所以\(\mu(i*l[j])=0\),否则，说明\(i*l[j]\)中的本质不同质因子个数比\(i\)多了\(1\)，所以\(\mu(i*l[j])=-\mu(i)\)

for(int i = 2; i <= n; i ++) {
    if(!p[i]) l[++ l[0]] = i, mul[i] = -1;
    for(int j = 1; j <= l[0] && i * l[j] <= n; j ++) {
        p[i * l[j]] = 1;
        if(i % l[j]) {
            mul[i * l[j]] = -mul[i];
        }else {
            mul[i * l[j]] = 0;			
            break;
        }
    }
}

code

P2158 [SDOI2008] 仪仗队

求\(\sum_{i=1}^{n}\sum_{j=1}^{n}[\gcd(i,j)==1]\)

转化成\(\sum_{i=1}^{n}\sum_{j=1}^{n}\epsilon(\gcd(i,j))\),然后根据\(\mu*1=\epsilon\),然后卷积得到：

\[\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{d|\gcd(i,j)}\mu(d) \]

根据一个常见的套路，就能得到：

\[\sum_{d=1}^{n}\mu(d)\lfloor\frac{n}{d}\rfloor\lfloor\frac{n}{d}\rfloor \]

那么问题就转化成线性求\(\mu\)了，那么答案已经在上个题解了

code

8.10

CF1238D AB-string

题目简述：给定一个只有\(A,B\)构成的字符串\(S\)，定义一个良好的字符串为，该字符串中每一个字符能被至少一个长度大于\(1\)的回文串覆盖。要求求出 \(S\)中所有良好的子串 \(|S|\le 1e6\)

正所谓：正难则反，考虑计算出所有不良好的子串，那么思考不良好的子串有什么特征或性质。发现\(S\)中只有\(A,B\)，那么不难发现，不良好的情况只有为\(ABB\cdots B,BAA\cdots A,AA\cdots B,BB\cdots A\)的情况，所以直接枚举所有连续的子段就行（考场上没想出来TAT）

code

8.11

P4777 【模板】扩展中国剩余定理（EXCRT)

注意：要用__int128,要写快读快写。

题面：中国剩余定理的模数不一定互质版

题解：抽离出两个来

\[\begin{equation} \left\{ \begin{aligned} & x\equiv b_1\mod a_1\\ & x\equiv b_2\mod a_2\\ \end{aligned} \right . \end{equation} \]

考虑把他们两个合并：

\[\begin{equation} \left\{ \begin{aligned} & x+y_1a_1= b_1\\ & x+y_2a_2=b_2\\ \end{aligned} \right . \end{equation} \]

发现有两个\(x\)，因此可以当作中间量得到：

\[\begin{aligned} b_1-y_1a_1&=b_2-y_2a_2\\ &\Downarrow \\ y_2a_2-y_1a_1&=b_2-b_1 \end{aligned} \]

那么就可以用ex_gcd求\(y_1,y_2\)了，得到

\[x\equiv b_1-y_1a_1 \]

要考虑最小解，所以要给\(x\)加一些数，为了使两个条件都得到满足，所以加得数就是\(lcm(a_1,a_2)\)，所以最终的式子为：

\[x\equiv b_1-y_1a_1\mod lcm(a_1,a_2) \]

与下面式子继续合并即可\

判无解的条件：就是方程无解的时候

code

P2444 [POI 2000] 病毒

注意：\(AC\)自动机可能长成

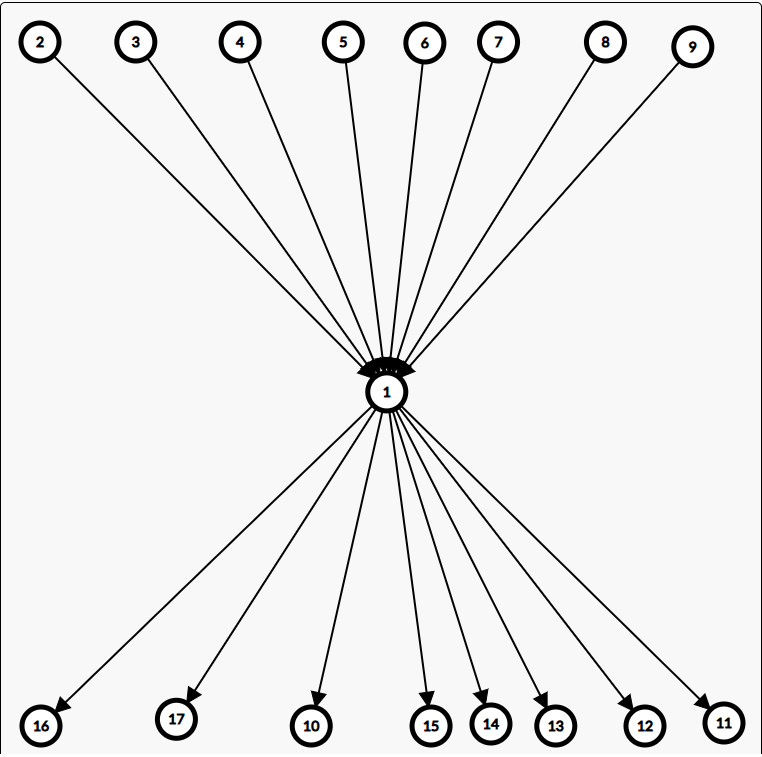
这个样子，那么枚举的时候就会重复遍历一个点多次，所以会\(T\)，解决办法就是经过一个点，如果没有环，就把该点设为无环的状态，搜索的时候搜索到无环状态直接返回即可

8.12

P5824 十二重计数法

前情提要：这里只给出式子，不会写代码

\(n\)个盒子， \(m\)个球，有十二个限制条件，求出每个限制条件下将\(n\)个球放到\(m\)个盒子里的方案数

\(I\):球互不相同，盒子互不相同：

每个球都可以放到\(m\)个盒子里，所以每个球的选择都为\(m\)个，答案就为\(m^n\)

\(II\)：球互不相同，盒子互不相同，每个盒子至多有一个球：

比较显然的是，\(n>m\)的时候答案为\(0\)，当\(n\le m\)时，一个球占据了一个盒子后，其他球就不能再在这个盒子里放了，也就是，第一个球有\(m\)个选择，第二个球有\(m-1\)个选择，以此类推，答案就是\(m^{\underline n}\).也可以理解为，在\(m\)个盒子里选\(n\)个盒子放球，球互不相同，所以有\(n!\)个放球的方案，最终答案为\(\binom{m}{n}n!\)，两者是等价的

\(III\):球互不相同，盒子互不相同，每个盒子至少有一个球：

至少有一个球的意思就是所有盒子都不为空，那么正难则反，考虑用所有的方案减去有空盒子的方案，比如，钦定一个盒子是空的方案数就是\(\binom{m}{1}(m-1)^n\)，那么，会迎来一个问题，会减多对吧，所以要加上有钦定两个盒子是空的方案，发现又加多了对吧，所以还要减，加，减\(\cdots\)，那么最终的答案就是 \(\sum_{i=0}^{m}(-1)^i\binom{m}{i}(m-i)^n\)

\(VI\):球互不相同，盒子全部相同，每个盒子至少装一个球:

发现其实就是第三种情况除以\(m!\)，因为盒子相同，因为\(m!\)的排列方案数就是一个方案。那么答案就是\(\frac{1}{m!}\sum_{i=0}^{m}(-1)^i\binom{m}{i}(m-i)^n\),那么发现这其实就是第二类斯特林数的定义式，所以答案也就是\(S(n,m)\)

\(I V\):球之间互不相同，盒子全部相同。

首先看到这个，一个错误的想法就是第一种情况除以\(m!\)，但发现不行，因为会有空的盒子，空的盒子在这种情况下就是本质相同的，那么怎么避免这种问题呢，发现\(VI\)中，可以直接除以\(m!\)的原因是因为每个盒子都有至少一个球，那么我们尝试推广一下，能发现，该情况的答案其实就是枚举有多少个盒子是空的，剩下的都不为空的方案数加起来，也就是\(\sum_{i=1}ans(VI_{n,i})\),那么答案就是\(\sum_{i=1}^{m}S(n,i)\)

\(V\):球之间互不相同，盒子全部相同，每个盒子至多装一个球。

这个比较好想啊，当\(n>m\)的时候答案肯定为\(0\)，当\(n\le m\)的时候答案就为\(1\)。

\(VII\):球全部相同，盒子之间互不相同。

这个就是插板法，但是可以为\(0\)，所以答案为 \(\binom{n+m-1}{m-1}\)

\(VIII\):球全部相同，盒子之间互不相同，每个盒子至多装一个球。

一样的,\(n>m\)答案为\(0\), \(n\le m\)的时候相当于在\(m\)个盒子里选出\(n\)个盒子放一个球的方案数，也就是\(\binom{m}{n}\)

\(IX\):球全部相同，盒子之间互不相同，每个盒子至少装一个球。

这个是裸的插板法，答案为\(\binom{n-1}{m-1}\)

\(X\):球全部相同，盒子全部相同。

相当于把\(n\)划分成\(m\)个自然数之和，然后这\(m\)个数是单调不降（升）的，就是数的划分

\(XI\):球全部相同，盒子全部相同，每个盒子至多装一个球。

和\(V\)是一个答案，即\([n\le m]\)

\(XII\):球全部相同，盒子全部相同，每个盒子至少装一个球。

相当于把\(n\)划分为\(m\)个正整数之和，然后这\(m\)个数是单调不降(升)。数的划分

数的划分：（自然数版）

题目： 用\(m\)个数拼成\(n\)
设\(f_{i,j}\)为当前拼出来和为\(i\)，用了\(j\)个数的方案数，那么可以给这\(j\)个数都加\(1\)，也可以再用一个为\(0\)的数，也就是

\[\begin{equation} f_{i,j}\to\left\{ \begin{aligned} f_{i+j,j}\\ f_{i,j+1} \end{aligned} \right . \end{equation} \]

最终输出\(f_{n,m}\)即可

正整数就是把\(f_{i,j}\to f_{i,j+1}\)变成\(f_{i,j}\to f_{i+1,j+1}\)

8.13

P6521 [CEOI 2010] pin (day2)

容斥的题

题面：找出有多少对字符串满足恰好\(D\)个位置对应的字符不相同，字符串长度等于\(4\)

首先不相同可以转化成相同，即恰好\(4-D\)个位置相同，恰好这个条件很难满足，直接说结论要用容斥，我们设\(f_i\)为钦定\(i\)个位置相同的字符串对数，那么答案为\(f_D-\sum_{i=4-D+1}^{4}(-1)^{i-D}f_i i\),其中乘上\(i\)的原因是钦定\(i\) 个位置相同的字符串对数会在\(i-1\)里被重复算\(i\)次。还要特判一下\(D=4\)的情况，就是用所有的字符串对数减去恰好\(1,2,3,4\)个字符串相同的对数

8.14

四元环计数

无向图\(G\)的一个四元环指的是一个\(G\)的子图\(G_0\)，满足\(G_0\)有且只有\(4\)个点\(a,b,c,d\),有且只有四条边\(\left\langle a, b\right\rangle,\left\langle b, c\right\rangle,\left\langle c, d\right\rangle,\left\langle d, a\right\rangle\)。两个四元环\(G_1,G_2\)不同当且仅当存在一条边\(e\)满足，\(e\in G_1,e\notin G_2\)。

说在前面：四元环计数是由三元环计数推出来的，所以先讲三元环计数。

三元环计数：

暴力枚举是\(n^3\)的，考虑优化啊，然后有一个神奇的做法，把每一个边定向，使得每条边都是从度数小的点指向度数大的点，那么三元环上就会变成\(小\to中，中\to大，小\to大\)，所以可以枚举小的点，然后枚举其出边指向中的点，最终枚举中的点指向大的点，然后判断小和大之间是否由连边，然后就好了。细节：如果两个点的度数一样，那么就让编号小点指向编号大的点。

复杂度证明：乍一看感觉还是\(n^3\)的，但实际上是\(m\sqrt{m}\)的。首先枚举小的点和其出边是\(O(m)\)的，然后看中的点，分两种情况，如果中的点的度数是小于等于\(\sqrt{m}\)那么遍历就是\(\sqrt{m}\)的，如果大于\(\sqrt{m}\)，那么因为有向边指的是更大的点，并且最多会有\(\sqrt{m}\)个点的度数大于等于\(\sqrt{m}\)，所以枚举出点也是\(\sqrt{m}\)的，所以就证明了复杂度了

四元环计数：

根据上面的经验，我们依旧将无向图改为\(DAG\)，那么通过手模，可以发现，四元环的指向关系只有\(3\)种本质不同的情况，详见下图：

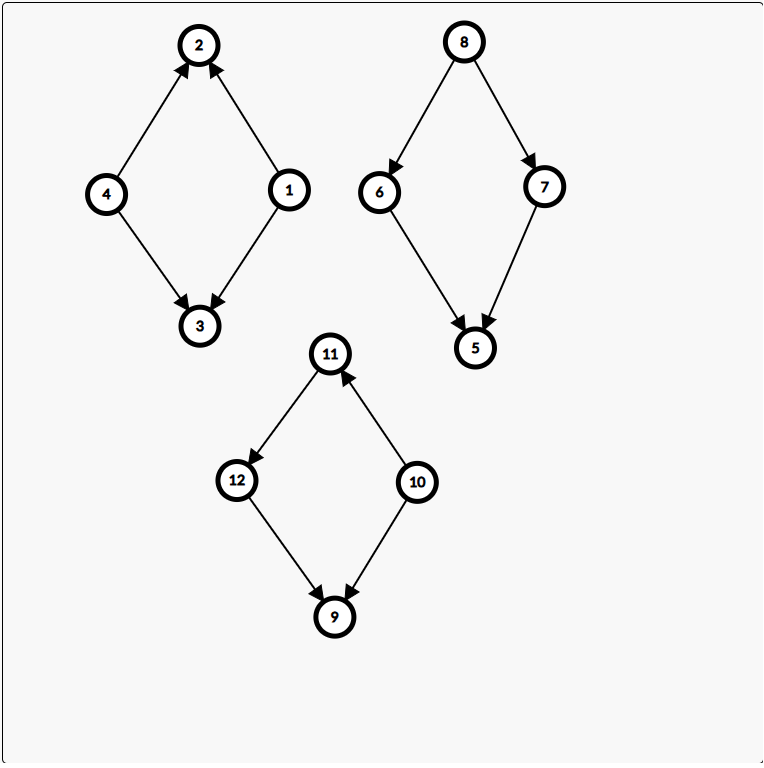
然后呢，能发现，这三张图都有共性，就是下方的点都是被指的，但是上方的点的指向是不规则的，那么，又有一个比较厉害的做法，就是从一个点开始，先走一条无向边，再走一条有向边，这样，对于每一个起点维护一个终点出现次数的数组，比如，从\(2\)开始，能走到\(3,x\)次,那么，这样的四元环就是\(\binom{x}{2}\)，但是，会发现，左上角的情况会被算两遍，就是在\(2\)的时候计算\(3\)一次，\(3\)计算\(2\)一次。那么我们考虑再次加强限制，能发现，其他的两种情况起点的度数一定比终点的度数要小，所以，我们以这个为限制，让终点的度数大于起点，这样就不会算重了。

code

CF1828B2

很精彩的一道题
当\(k\)是奇数的时候答案是\(1\)，可以手模出来
首先定义好边，好边定义为两个端点都是好点的边，那么能瞪出来一个性质，就是好边的左右子树的人数相同。那么根据此性质，可以证明出所有的好边构成了一个连通块，如何证呢？考虑由两个处于两个好边组成的连通块中的好边\(A,B\)，\(A\)下端的子树中人的个数为\(a\), \(B\)的为\(b\),剩下的的部分为\(c\)，那么能得出\(a=b+c,b=a+c\to b=b+c+c\)，解出\(c=0\)，所以两个连通块之间都没有人，所以两个连通块之间的边都是好边，所有构成了一个连通块。
由于好边两边的子树里的人数相同，所以就为\(\frac{k}{2}\)个人，那么考虑一个边的贡献就是他两边个都为\(\frac{k}{2}\)的方案数除以总方案数(设左边为
\(siz_1,siz_2\))$$\frac{\binom{siz_1}{\frac{k}{2}}*\binom{siz_2}{\frac{k}{2}}}{\binom{n}{k}}$$。但是呢，答案要求的点的期望，然后，就用到证明的性质，因为连通块的点数是边数加一,而期望又具有线性性，也就是\(E(点数)=E(边数+1)=E(边数)+1\)，所以答案就是边数的答案加\(1\)

8.17

CFgym104023I

题目：一个物品需要\(n\)种精华生成，每种精华所需要的数量是\(a_i\)个。现在有\(k\)种工具，第\(j\)个工具可以生产任意\(2^{j-1}\)个精华，要求求出最多可以生成多少个物品

贪心：因为多个小的可以凑成大的，但是大的不可以拆成小的，也就是说小的比大的灵活，所以有一个贪心思路，就是优先用大的拼大的精华，然后大的用完了就用次大的精华。具体的，因为要求个数，然后发现个数具有单调性，所以可以二分答案，二分答案后，将\(n\)种精华需要的数量放到一个大根堆里，然后不断地弹出堆顶，优先用大的精华，然后，就没了。

sez157

题面：给定一个张\(9\)个点的有向图，每条边有一个优先级 \(p\)，和花费\(w\)，有\(q\)个询问，每个询问给出\(z, t, s\)，和\(s\) 个区间\(l_i,r_i\)，要求，从\(z\)走到\(t\)的最小花费\(min_w\)，其中，走过的边的优先级必须单调递增，并且优先级必须在 \(l_i, r_i\) 区间内。具体的，设从\(z\)走到\(t\)的边上的优先级分别为\(p_1, p_2,p_3\)，则\(p_i\in[l_j,r_j]\)，\(p_i\le p_j\)

首先考虑没有优先级的限制，那么这道题就是裸的最短路，用\(Floyd\)就可以直接写了。

然后考虑如果只有一个优先级，那么其实就是相当于在一个优先级上跑\(Floyd\)就行了。

进一步，考虑有一个连续的优先级怎么办。这个就需要有点厉害的思路了。我们设\(f_{p,u,v}\)表示从只在优先级是\(p\)的边上跑，从\(u\to v\)的最短距离，那么这个其实就是上面的答案，那么考虑\(g_{p,u,v}\)表示在优先级\(\le p\)的边上跑，从\(u\to v\)的最小花费。那么考虑如何得到\(g\)。思考还有个限制是优先级递增，那么走过的边必定有一个断点，从这个断电之后的边的优先级都是\(p\)，根据这个思路，我们可以得到\(g\)的式子：$$g_{p,u,v}=\min_{k\in [1,9]}(g_{p-1,u,k}+f_{p,k,v})$$
得到这个式子后还没完，我们发现这个东西，很像矩阵乘法，也就是把矩阵乘法里的乘法重定义为加法，将加法重定义为取\(\min\)操作。这个东西是满足结合律的，（同理，加法取\(\max\)操作也满足结合律），那么，结合题目说的有多个区间，那么就能想到用线段树维护矩阵（真是天才想法）

code

8.18

gym105578E

题意：有一个游戏，\(2\times 2\)的网格，每个格子有两个状态\(0,1\)，\(0\)代表开启，\(1\)代表关闭，每次可以进行以下操作，直到网格中每个格子都变成\(1\)。

• 将单个格子异或\(1\)，代价为\(a_0\)
• 将一行格子异或\(1\)，代价为\(a_1\)
• 将一列格子异或\(1\)，代价为\(a_2\)
• 将所有格子异或\(1\)，代价为\(a_3\)

现在有\(m\)种网格，要求输出一种操作序列，使得任意网格能在操作过程中曾经达到结束状态。求出代价最小的操作序列

发现这道题难搞的就是\(m\)种网格，因为操作一次所有网格都会改变形态。但是，网格只有\(4\)个格子，所以最多会有\(16\)种格子，也很小。我们整合一下信息，发现有代价，需要求最小值，有多个状态，一个状态可以通过几个变换到达其他状态。结合这些信息，其实可以想到状压一下然后建出图来跑最短路。又因为可能有多个格子一起转移，所以实际上会状压出\(2^{16}\)种状态。对于四种变换都连一条边，然后跑最短路。

具体的：设\(S\)集合表示若干个网格，设\(S'\)为\(S\)进行任意变换后得到的新的网格集合。因为要求网格在操作过程中曾经变成过结束状态，所以\(S'\)中如果有结束状态的网格，那么就直接把它从集合中踢去，然后接着转移。在代码中提现就是\(S'\)中代表结束状态的位置始终是\(0\)，这样就可以了。最终转移到全零的状态即可

注意：

因为题目要求在操作后得到终止状态，所以初始给的网格如果包含终止状态是不算的，需要将终止状态进行变换然后的到全零状态。但是，这个实际上是不影响算法流程的，因为只要有一个网格进行变换，那么该集合中所有的网格包括终止状态都会发生变换，而最后要转移到全零状态，所以，转移过程中一定会把终止状态进行变换，所以不需要特判什么的。

code

HDU

题意：给定一张有向有权图，求出该图的第\(k\)小的路径

说这个之前，先说给定一个长度为\(n\)的序列如何求第\(k\)小的子集。暴力做法就是首先对原序列进行排序，然后先将第一个数放到堆里，然后每次取出堆顶，记录堆顶代表子集的最后一个数的位置，然后枚举后面的每一个数，把他放到这个子集后面，然后塞入堆里。 第\(k\)次取出的就是第\(k\)大。

首先这个是可以枚举到每一个区间是没有问题的，但是时间复杂度和空间复杂度都会炸，考虑优化。有一种和这个等效的做法是，把堆顶取出后有两种操作，第一个是在他后面加上一个数，第二个是将这个子集最后一个数删去，然后新加一个数。两个实际上是等效的。然后时间复杂度可以优化到\(O(\log(n+k)(n+k))\)了。是可以接受的。

然后这个问题也是一样的，只不过是把最后一个边删去，然后加上相连的边就好。代码实现有点细节需要思考思考。

8.19

sez169

给定一张\(n\times m\)的网格，有\(k\)个起点，\(q\)个障碍物。定义一个点为坏点为：点\(i\)到\(k\)个起点的最短路最小值不唯一。求坏点的数量

多源\(BFS\)，从多个起点开始\(BFS\)，把多个起点一起放到队列里，然后，一个点为坏点为，两个不同的起点最先用相等的最小值更新了他；由另一个坏点更新了他（因为可能该点其他三个相邻的点都是障碍物，只有坏点与他联通）。然后正常\(BFS\)就行

code

CF1622F Quadratic Set

题目：定义一个正整数集合为"二次集"，当且仅当集合中元素的阶乘之和为平方数，即\(\prod_{i=1}^{k}a_i!=m^2\)。现在，要求求出\(1,\dots,n\)这个集合的最大规模的二次子集

碰到这种题，有一种思路是求出答案的下界或上界，然后再暴力做，怎么猜呢，凭感觉，多大能过猜多少，乐。

说结论：答案的下界为\(n-3\)
证明:首先设\(x=\prod_{i=1}^{n}i!\)

1. 当\(n\)为偶数时：
   • 发现\(1,\dots,n\)奇数都被乘了偶数次，偶数都被乘了奇数次，那么把奇数都提出来，都能得到一个平方数，接着把偶数的偶次幂也提出来，也得到一个平方数，这些都可以不管了直接扔掉，最终得到\(2\times4\times6,\dots\),继续提一个\(2\)得到\(2\times (\frac{n}{2})!\)。这样，把\(x\)除以\(2!\)和\((\frac{n}{2})!\)就能得到一个平方数
2. 当\(n\)为奇数时：
   • 直接将\(x\)除以\(n!\)，然后转成偶数就行了

得到这个性质，那么我们考虑如何求出到底是\(n,n-1,n-2,n-3\)。发现暴力判是不是平方数是不可行的，因为会爆long long。考虑继续优化。思考，平方数有什么性质，即是，平方数的每一个质因子的幂都是偶数。那么，实际上我们只关注质因子次幂的奇偶性。得到这个性质，那么就能想到，可以通过异或操作来记录到底是不是偶次幂。具体的，对于一个数，他的值就是他所有质因子的异或，例如，\(8\)的值为\(2\oplus 2\oplus2=2\)。如果最终的异或为\(0\)，那么就是平方数，否则不是。例如\(4\)的值为\(2\oplus 2=0\)是平方数。

有了异或这个利器后，考虑如何统计答案。

1. 判断是否是\(n\)，只需要判断所有阶乘的异或是否为\(0\)
2. 判断是否是\(n-1\)，首先将所有阶乘异或起来，然后判断是否有任意一个阶乘的异或等于它
3. 判断是否是\(n-2\)，将所有阶乘异或起来，然后将\(n-1\)个数的阶乘异或放到一个桶里面，然后枚举每一个阶乘，判断他的异或是否在桶里面。如果不太好理解，可以看看代码。
4. 当上面三个都不行的话，那么直接按照\(n\)为奇数的时候构造就行了。答案就是除去\(2,\lfloor\frac{n}{2}\rfloor,n\)的子集

注意：上面的过程有一个巨大的问题：

发现出题人有办法卡做法。因为如果有两个不同的质数异或起来刚好等于另一个质数，例如，\(2\oplus 5=7\)，那么\(70\)会被判成平方数，这样答案就是错的。但是这种方法还是可以用的。方法就是给每一个质数随机一个权值，这样异或起来大概率不会被卡。那么就可以过了。但是，用一个\(rand\)，最大的随机数\(32767\)，但是\(n\le 10^6\)，所以会出现冲突，所以要将\(rand\)变大，最好变到\(10^{18}\)，如何做呢，详见代码

小tips:

如何求出每一个数的异或值呢。发现如果\(a\times b=c\)，那么\(c\)的异或值就等于\(a\)的异或值异或\(b\)的异或值。那么考虑用线性筛来做。如果是质数的话，给他随一个值，不然就把\(i\times pri_j\)的值赋成\(i\)的值异或\(pri_j\)的值

code

CF516D Drazil and Morning Exercise

题意：给定一棵树,定义\(f_x=\max_{i}dist(x,i)\)。\(q\)次询问，每次询问给出一个\(l\)，要求求出最大的连通块点集\(S\)，满足\(\max_{x\in S}f_x-\min_{x\in S}f_x\le l\)。输出该连通块的大小。

循序渐进，暴力做法：考虑每个点的\(f_x\)作为最小值的最大连通块大小。发现只需要\(O(n)dfs\)一下就能找到连通块大小。时间复杂度\(O(qn^2)\)，考虑如何优化。俗话说得好, 树上问题，选一个好根很重要。那我们直接找到最小的\(f_x\)作为根，然后观察出有什么性质。发现\(f_x\)是\(\max_{i}dist(x,i)\)，那么，从\(x\)开始向下遍历，\(f_y\)一定是递增的，（有点忘了怎么证了，等脑子清晰了回来证一下）。有了这条性质有什么用呢。发现好像对复杂度没有什么实质性的优化。实则不然，如果这样，那么一个连通块肯定是几个链拼起来。那么我们继续转化，我们考虑，一个点\(x\)，能作为多少个点的\(\max\)值，发现，满足\(f_x-l\le f_y\)的\(y\)都可以，并且\(y\)组成了一个链，所以就可以做一个树上差分，然后就能发复杂度降到\(O(qn\log n)\)了

code

9.1

sez188

题目简述：给定一个长度为\(n\)的序列\(a\)， 每次操作可以选择一个\(i,1\le i\le n - 2\)，使得\((a_i, a_{i+1}, a_{i+2})\),变成\((a_{i+1},a_{i+2}, a_i)\)。要求构造出一种方案，使得操作完的序列最终升序排列。操作次数小于\(n^2\)次。如果没有方案输出“\(-1\)”

题解：

首先考虑序列是一个排列的情况。有一个构造方法（不知道怎么想出来的），就是将\(1\)放到第\(1\)个位置，将\(2\)放到第\(2\)个位置，直到将\(n-2\)放到第\(n-2\)个位置，然后，考虑\(n-1\)和\(n\)这两个位置的元素，设其分别为\(a,b\)，如果\(a<b\)那么无事发生，如果\(a>b\),考虑是否有解：对于构造题，通常设一个函数来判断是否有解，那么这里设\(f\)函数为\(-1^{\text{逆序对数}}\)，不难发现，目标状态，也就是升序状态的\(f=1\)，但是如果考虑序列有上述情况，那么\(f=-1\)，然后呢，题目给的操作实际上是进行了两次交换，而，一个序列中两个数进行交换，逆序对数奇偶性会改变，所以交换两次逆序对数的奇偶性不会改变。也就是说，初始状态的\(f=-1\)，所以初始状态和目标状态的\(f\)函数不同，那么也无法通过操作得到目标状态。

其次，如果不是一个排列，那么首先可以离散化一下，如果是排列，就按照刚才的做法做。如果不是排列，那么给相同的数分配不同的排名，比如\(1,2,2\)分配的排名为\(1,2,3\)，\(1,1,2\)分配排名为\(1,2,3\)，然后继续按照上面的操作做。如果出现的第\(n-1\)个元素大于第\(n\)个元素的情况，首先判断它俩相不相同。如果不相同就去找前面的是否有两个相同的元素，然后通过操作把两个相同的元素交换，然后将第\(n-1\)个元素和第\(n\)个元素交换。

code

题解

sez185

题目简述：给定一个长度为\(n\)的序列\(a\)，求出对于每一个\(i\)来说有多少个子序列\((a_{j_1},a_{j_2},a_{j_3},\dots,a_{j_k})\)，满足\(j_1<j_2<j_3<j_k=i\)，并且二进制位上满足\(a_{j_1}\subseteq a_{j_2}\subseteq a_{j_3}\subseteq\dots a_{j_4}\)。其中\(n\le 10^5,0\le a_i < 2^{16}\)

在引入题解前，先讲如何枚举一个数的二进制子集和包含他的二进制集合：

枚举二进制子集：

假设要枚举数\(mask\)的子集，算法流程如下：

vector<int> subset;
int x = mask;
while(x) {
  subset.push_back(x);// x就是mask的二进制子集
  x = (x - 1) & mask;
}

而算法的正确性体现在两方面：

1. 枚举出来的\(x\)一定是\(mask\)的子集，这点在\(\text{&}mask\)时保证了
2. 能枚举全，因为\(x\)时\(mask\)的子集，那么只需要保证新求出来的子集是比\(x\)小，且距离\(x\)最近的子集即可。\(-1\)保证了比\(x\)小。考虑\(-1\)在二进制下的意义，其实是把\(x\)中最小的\(1\)变成\(0\)，并且把其后的\(0\)都变成\(1\)，而这样就能保证是距离\(x\)最近的。

枚举包含他的二进制集合：

同理，枚举包含数\(mask\)的集合：

vector<int> set;
int x = mask;
while(限制条件) {
  set.push_back(x);
  x = (x + 1) | mask;
}

与上一个原理相似，不在赘述，看代码理解；

注意：限制条件一般为\(x\)最大能到哪

我们循序渐进：

1. 暴力做法，设\(f_i\)表示\(i\)的答案，那么可得转移方程：\(f_i=\sum_{j=1}^{i-1} f_j[a_j\subseteq a_i]\)，属于是\(O(16n^2)\)的
2. 考虑在转移方程中直接枚举\(a_i\)的子集，设\(g_s\)为所有\(a_j=s\)的\(f_j\)之和。那么转移方程就是\(f_i=\sum_{s\subseteq a_i}g_s\)，更新完\(f_i\)后，\(g_{a_i}+=f_i\)。\(O(n2^m)\),\(m=\log\max a_i\)
3. 上面是填表法，这次考虑刷表法，这次设\(g_s=\sum_{a_j\subseteq s}f_j\),那么转移方程就是\(f_i=g_{a_i}\)，\(g_s+=f_i(a_i\subseteq s)\)。\(O(n2^m)\)
4. \(2,3\)两个方案，当\(m=8\)的时候是可以过的，而\(m\)最大为\(16\),刚好一半，这让人联想到折半。考虑如何结合一下两种方法。首先肯定要把\(g\text{和}a_i\)分成两半，一半小于\(2^8\)，一半大于\(2^8\)。那么现在需要一种合适的方案使得转移和更新的最高复杂度为\(2^{m/2}\)，也就是\(2^8\)，如果一个是\(O(1)\)，那么另一个就是\(2^{m}\)，(也就是\(2,3\)两种做法)，所以只能是两个都是\(2^8\)，也就是两种算法给转移和更新平摊一下。那么我们就设\(g_{s,t}=\sum f_j[a_j>>8=s,a_j\text{&}(2^8-1)\subseteq t]\),对于一个\(i\)，设\(S=a_i>>8,T=a_i\text{&}(2^8-1)\)，那么转移为：\(f_i=\sum_{s\subseteq S}g_{s,T}\)。更新为:\(\forall T\subseteq t,g_{S,t} += f_i\).\(O(n2^{m/2})\)可过

code

sez163

题目简述：给定一个数组\(a\),一开始元素都为\(0\)，还有一个数组\(p\)，现在给定两种操作，第一种操作给定\(l,r,x\),将所有\(l\le i\le r\)，\(a_i+=x\)。第二种操作给定\(l,r\)，求出\(\sum_{i=l}^ra_i\)。强制在线。

提供一种在一个区间内用\(\log\)的时间复杂度，\(O(n)\)的空间复杂度找出值域在\([l,r]\)内的数的个数\((-\infty\le l < r\le \infty)\)。就是把原区间排序，然后\(\operatorname{upperbound(r)}-\operatorname{lowerbound(l)}\)就行。

题解：

将两个数组分块，然后想办法维护每个块的总权值（想了我老半天），和单独一个数的值就行。重要就是维护\(p\)数组分完块后每个块个值。那么对于每个块，只需要找出有多少个在\(l,r\)区间内的个数在乘上\(x\)就行。然后就没了。。时间复杂度\(O(n\sqrt{n}\log\sqrt{n})\),虽说不应该过的，但是还是卡过去了

code

9.2

sez189

题面
这里面有重要的性质：没有吃到的\(husky\)是连续的。那么实际上只需要考虑一个点是否能吃到就行。

一开始想的是\(O(n)\)遍历，\(O(\log n)\)判断是否能吃到。但想了半天也没想到。但是没有充分利用连续这个条件。因为连续，所以相当于就有了单调性，所以可以直接二分，所以可以\(O(n)\)判断是否能吃到了。因为是连续，所以二分出\(mid\)前一定是都能吃到，然后如果其\(m\) 小于\(mid\)，那么就直接扔到后面不管就行。否则就先留着，将能放的都放进去，然后再判断是否能扔进去。如果都能被扔进去，那么说明正确答案要再小一些，反之亦然。

code

开快读优化输入输出

9.3

sez692

题面简述：给定一个迷宫，起点不固定，询问有多少种不同的合法路径。路径合法当且仅当：

• 只能走上下左右四个格子
• 只能走相邻数字中比当前格子恰好大\(2\)的格子
• 路径长度至少为\(4\)
• 如果周围还能继续走，那就必须继续走
• 起点周围不能有比该格子恰好小\(2\)

爆搜可能出现一个点被重复遍历好几次的情况，所以可能会爆。所以考虑优化。
记忆化搜索就是好！！！：记录一个\(num_{x,y,1/2/3/4}\)数组代表从\((x,y)\)为起点，长度为\(1,2,3\)和大于\(4\)的路径数一共有多少就行了。然后就直接做。

不过oj上的数据太水，爆搜也能过。

code

9.4

sez693

写在前面：熟练运用对顶堆。最需要注意的就是，当在对顶堆插入一个元素\(x\)时，要判断\(x\)与大根堆堆顶的关系，然后再决定\(x\)放到那个堆中。其次，时时记着维护大根堆中的元素个数，例如，如果动态维护第\(k\)大，那么在\(k\)更改的时候就是该维护一下大根堆中的元素，然后再进行其他操作。

题面：给定一个长度为\(n\)序列\(a\)，可以进行两个操作：

• 选择一个\(i(1\le i\le n)\)，使得\(a_i\)变成\(a_i+2\)
• 选择一个\(i(1\le i\le n)\)，使得\(a_i\)变成\(a_i-1\)

要求求出最少多少次操作能使序列\(a\)变成一个特殊的等差序列；特殊等差序列的定义为，至少存在\(n-2\)个\(i(2\le i\le n)\)满足,\(a_i-a_{i-1}=d\)。

题面比较简洁，题解就不是了。首先介绍一下带权中位数

带权中位数：

对于一个序列\(c\)，要使得\(\sum |x-c_i|\)最小,那么\(x\)肯定是取该序列的中位数。但是要使得\(\sum_{x<c_i}(c_i-x)+\sum_{x>c_i}\frac{x-c_i}{2}\)最小呢？考虑现在已经固定了一个\(x\)，设比\(x\)小的数为\(n-a\)个，比\(x\)大的数有\(a\)个，那么如果把\(x+1\)，那么整体的贡献就会\(-a+\frac{n-a}{2}\)，当\(x\)从\(0\)开始变大，那么这个贡献会先为负数，然后变成正数，贪心的想，我们就是需要找到变化恰好为\(0\)的时候，也就是\(a=\frac{n-a}{2}\)解一下就能得到\(a=\frac{n}{3}\)，所以\(x\)要取的位置就是\(b_{n-\lceil\frac{n}{3}\rceil+1}\)这个位置，（\(b\)数组为\(c\)数组从大到小排完序的数组),解释一下：取上取整和加一都是因为左边会乘\(\frac{1}{2}\)，所以贡献就相当于\(-\lceil\frac{2n}{3}\rceil+\lfloor\frac{n}{3}\rfloor<0\)，所以更优。

题解：

首先经过不知名算法得到公差的上界\(n*d\le M=2*10^6\)。
考虑只有一个等差数列的情况。知道了公差的上届，所以可以直接枚举公差\(d\)，当知道了\(d\)以后，现在只需要选取一个合适的首项\(x\)即可。对于第\(i\)项\(a_i\)，\(a_i=x+(i-1)*d\)，我们令\(c_i=a_i-(i-1)*d\)，那么只需要调整\(c_i\)到\(x\)即可，那么操作次数就约为：\(\sum_{x<c_i}(c_i-x)+\sum_{x>c_i}\frac{x-c_i}{2}\),根据带权中位数得知，\(x\)取到\(b_{n-\lceil\frac{n}{3}\rceil+1}\)即可。
但是题目说的是要求两个等差数列，那么对于每一个\(d\)，分别维护一个前缀最小值和后缀最小值，最后拼起来即可。其中，又因为要动态维护第\(k\)大，所以需要利用到对顶堆。

注意：即使找出了首项\(x\)，但是对于\(c_i<x\)的部分，当\((x-c_i)\equiv 1\pmod 0\)时，操作中需要先进行一次操作，将\(c_i-1\)，所以在维护对顶堆的时候还需要知道偶数和奇数的个数，同时，因为分奇偶，所以\(x\)要取\(x-1,x+1\)分别计算最小值，否则会错。

其余的就很好办了，只需要维护小于\(x\)的元素和，大于\(x\)的元素和即可。

时间复杂度\(O(\frac{M}{N}*N\log N)=O(M\log n)\)

9.5

P4859 已经没有什么好害怕的了

题面简述：给定\(a\)，\(b\)两数组，需要将两个数组两两配对，求\(a_i>b_j\)的对数恰好为\(k\)的方案数，\(\forall i,j\quad a_i\ne b_j\)

看到了恰好，因为恰好一般比较难做，所以就转成钦定来做，也就是二项式反演了。设\(g_k\)为钦定对数为\(k\)个，\(f_k\)为恰好为\(k\)个，那么就能通过二项式反演互相求了。主要是\(g\)如何求。发现\(g_k\)就等于在\(n!\)个配对里面找出\(k\)个配对恰好为\(a>b\)的方案数乘上\((n-k)!\)，那么前者可以直接通过\(dp\)求得。那么就比较板了。

总结：遇到恰好就要联想钦定。

code

P3216 [HNOI2011] 数学作业

题目简述：求将\(1\)~\(n\)顺次拼接后的形成的数对\(m\)取模后的值。

感觉像是一种类型的题目，所以就直接写题解了

题解：发现答案可以写成\(\sum_{i=1}^n (x*(\lfloor\log i\rfloor + 1) + i) % m\)，直接做肯定是不行的。然后我们考虑用矩阵优化。那么很容易就构造出来转移矩阵：

\[\begin{vmatrix} 10^{\log i +1} & 0 & 0\\ 1 & 1 & 0\\ 0 & 1 & 1 \end{vmatrix} \]

那么发现这里面有个变化的量，\(\log i\)。解决方法呢，发现\(\log i\)最大是\(18\)，并且一个\(\log\)对应的是一个连续的区间，所以可以直接枚举断点，求出次数，就完了

总结：如果找到了线性递推式，但是要求在小于线性的复杂度内完成，那么可以考虑构造出初始矩阵和转移矩阵，然后通过矩阵优化完成题目。例如P1962 斐波那契数列, 和P4007 小 Y 和恐怖的奴隶主

code

还有需要注意时刻取模

P5505 [JSOI2011] 分特产

二项式反演题。题面相当于恰好\(0\)个人没有分到。出发关键词，直接反演。

注意：开数组的时候要看实际大小使用多少。例如如果调用了\(fact[a_j+num]\)，那么就要看\(a_j\)和\(num\)的大小

总结：对于一些题目，不一定有明确的“恰好”，“钦定”，这时要转化题意，比如这里，每个同学至少得到一个特产，那么转化后就会变成恰好\(0\)人没分到特产。

code

9.6

P3959 [NOIP 2017 提高组] 宝藏

首先一种错误的做法：（我想的）
首先枚举起点。对于一个起点，设\(f_i\)表示点集\(i\)中的宝藏都被选，最小代价，\(g_{i,d}\)，表示在\(f_i\)最小的时候，点\(d\)到起点的距离。转移为：

\[d\in i, to\notin i,d\in x, to\in x \]

\[ f_i+g_{i,d}*val_{d,to}\to f_x \]

\(g\)同理。

但这样是不对的。因为当有多个状态转移到同一个状态，并且代价相同，这样到起点的距离就无法统一计算。所以会被hack

解法：

上述方法的问题在于距离，那么考虑如何解决。因为是 \(dp\)，所以要把所有状态都枚举到，那么不妨，把距离设到状态里，设\(f_{i,len}\)，表示点集\(i\)都在距离为\(len\)前（包含\(len\)）选了。那么转移的时候枚举\(i\) 补集的子集即可。
但是问题又来了，现在相当于把\(i\)补集的子集都放在了距离为\(len + 1\)的位置，根据题意要求，\(len\)和\(len+1\)中间一定有连边，那么这就出问题了对吧。因为没有保证有连边。但是这个方法还是正确的。因为如果\(len+1\)和\(<len\) 中有连边，那么把他放到\(<len+1\)的位置一定更优，所以最终也一定是该状态取更新答案。正确性不会受影响。

总结：1. 在\(dp\)方程或递推式子中，如果有一个会随状态的转移而变化的量，首先考虑变化是否有规律，如果没有规律考虑把这个变量也放在状态里。2. 对于\(dp\)状态中不合法的转移，考虑这个转移会不会比原来更优，如果不会更优就不会对正确性产生影响，否则需要规避这种转移 3. 在图上\(dp\)，如果状态或转移有关拓扑序或深度，那么就可以考虑分层来解决

code

CF1614D1 Divan and Kostomuksha (easy version)

题目：给定一个序列\(a\)，要求重排序列使得\(\sum_{i=1}^{n}\gcd(a_1,a_2,a_3,\dots,a_i)\)，特别的规定\(\gcd(x)=x\)。

这道题呢，首先对答案打表，可以得到两个性质，前缀\(\gcd\)递减，并且后面的是前面的因数。（虽然后面的没一开始就发现），然后可以的得到一个会\(T\)的做法。
记录\(cnt_i\)表示是因数\(i\)的倍数的个数是多少。考虑从后向前填，然后\(dfs(pos, val, s)\)，表示当前在第\(pos\)个数，已经得到的值是\(val\)，结尾的\(\gcd\)为\(s\)，然后枚举\(s\)的倍数\(x\)，继续\(dfs(cnt_x,val+(cnt_s-cnt_x)*s,x)\)，当\(pos=0\)时结束递归，更新答案。
那么为什么会\(T\)，原因有两个。

1. 因为枚举\(s\)的倍数，所以会从\(2,3,4\)倍枚举，但是一些枚举是无效的，比如\(4\)倍, 发现\(dfs(pos,val,s)\to dfs(cnt_{4s},\dots,4s)\)，一定不必\(dfs(pos,val,s)\to dfs(cnt_{2s},\dots,2s)\to dfs(cnt_{4s},\dots,4s)\)优。所以前者就是无效的。那么为什么会出现这种情况呢。类比埃式筛和欧拉筛，一个数可能被多个数筛到，而又因为\(cnt_{s}\ge cnt_{ks}\)，所以在一个合数的倍数一定不必几个素数倍数优。那么就得到策略，每次只变成素数倍数即可
2. 但是，一个状态还是会被枚举很多遍。一个数可能是很多数的倍数，所以还是会炸。那么这时候就不妨考虑记忆化搜索或\(dp\)了。但是状态要记两维\(pos\text{和}s\)，不难发现\(pos\)实际没什么用处，因为\(s\)唯一对应一个\(cnt\)，所以可以只记录\(s\)即可。

这题的记忆化搜索需要注意，一开始实际上相当于记录了后缀和，但是后缀又会更改，所以记录的值相当于也会更改，所以记忆化的时候需要记录前缀，只需要改成\(dfs(cnt_x,x)\),当\(pos=0\)返回\(0\)，然后再加上贡献就行。

总结：1. 遇到\(\gcd\)，可以向因数，枚举最大公因数想。2. 状态转移的时候，不要无脑转移，思考是否有的状态无效或根本用不上，减少状态枚举数，使得复杂度减小。感觉也相当于剪枝

code

9.7

P4071 [SDOI2016] 排列计数

题面：求出长度为\(n\)的排列\(a\)，满足恰好有\(m\)个位置满足\(a_i=i\)。\(0<m\le 10^6,1\le n\le 10^6,T\le 10^5\)

题解：

本来一看有恰好想无脑二项式反演来着，一看数据范围。。只能说不能太懒。
那么如何做呢。发现恰好有\(m\)个位置满足\(a_i=i\)其实就是选定\(m\)个数，剩下的数不能有一个\(a_i=i\)。那么如果设\(g_i\)表示长度为\(i\)的排列满足没有一个数是\(a_i=i\)的个数，答案就是\(\binom{n}{m}*g_{n-m}\)。现在问题就成了如何求\(g\)了。因为数据是\(10^6\)，所以考虑线性递推。如果知道了\(g_{i-1}\)，那么有一种方案就是将\(i\)这个数与前\(i-1\)个数随意替换，也满足条件。\(g_i=g_{i-1}*(i-1)\)，但是这样就结束了吗？通过打表发现，这样实际上会算少。少考虑的部分是，如果前\(i-1\)个数恰好有一个满足\(a_j=j\)，那么可以将\(i\)与\(j\)互换，也是满足条件了。那么不妨设\(g_{i,0}\)为前\(i\)个有\(0\)个\(a_i=i\),\(g_{i,1}\)为前\(i\)个有\(1\)个\(a_i=i\).\(g_{i,1}\)，其实就是\(n=i,m=1\)时，答案就是\(\binom{n}{1}*g_{n-1,0}\)，所以最终的递推式子就为：

\[g_{i,0}=(g_{i-1,0}*(i-1)+g{i-1,1}) \]

\[g_{i,1}=g_{i-1,0}*i \]

题外话：

next_permutation(begin, end)可以直接生成下一个排列，比较好用，这道题的打表就是用这个的。

总结：多动脑，不要无脑做题；得到一个式子，可以通过暴力对拍的方式进行验证；

code

9.8

P6008 [USACO20JAN] Cave Paintings P

一些格子是等价的，也就是涂哪个都一样，我们把他们缩成一个点来考虑；两层之间的格子有限制关系，就是一个格子放水，另一个格子就必须放。发现，一个点，限制他的点最多只有一个。因为如果有两个及以上，那么说明这两个是互通的，那么这些点就会被缩成一个点。那么这就相当于森林。然后呢，问题就转化成，对一棵树，每个节点可以染色也可以不染色，如果父亲节点染色那么这颗子树都必须染色。求总的方案数。然后这个就是树形\(dp\)很好求。缩点使用并查集就可以维护

总结：熟练运用各类板子；如果有限制条件的话可以考虑连边转到图上做

code史山

P2606 [ZJOI2010] 排列计数

首先介绍\(lucas\)定理。当要求\(\binom{n}{m}\bmod p\)，\(p\in prime\)时，有\(\binom{n}{m}\equiv \binom{n/p}{m/p}*\binom{n\bmod p}{m\bmod p}\pmod p\)。会应用于两个场景。

1. 当\(n>p\)时，因为\(\binom{n}{m}=\frac{n!}{m!(n-m)!}\),有可能\(n!\equiv 0\pmod p\)，这时如果直接取模就会出错，所以要使用\(lucas\)定理
2. 当\(n\)过大，\(p\)比较小的时候，就可以把\(n,m\)的范围缩小了。

题解：

考虑有一个限制，\(\forall i\in [2,n],p_i>p_{i/2}\)，发现一个\(i\)唯一对应一个\(i/2\)，所以，又可以建出来图，而这个图是一棵树。对于节点\(x\)，\(x\)的孩子都比他大，所以要在可以的取值里取出\(siz_x\) 个数，并且让\(x\)当最小的内阁。而对于\(ls_x\)，他能够取到数的总个数就变成了\(siz_x-1\)，因为\(x\)这颗子树只能去\(siz_x\)个数。那么\(ls_x\)要选出来的数就是\(siz_{ls_x}\)个。然后套组合数乘一下就行。具体的，设\(f_x\)表示\(x\)这颗子树的方案数，那么\(f_x=\binom{siz_x-1}{siz_{ls_x}}*f_{ls_x}*f_{rs_x}%p\)，然后就没了

总结：有限制可以考虑建图；\(lucas\)定理应用于两个场景

code

10.16

Array Deletion Game

给定一个长度为\(n\)的数组，两个人轮次进行操作，每次操作为从数组的左端或右端取除一个元素，如果一个人去完后剩下的元素和\(\le s\)(\(s\)给定)，那么这个人就失败了。给定\(q\)组询问，每次询问给定一个\(s\)，回答是否有必胜策略。

博弈论的题，目前还不知道有什么规律，这里只给出题解：

定义合法区间\(l,r\)为\(a[l,r]>s\)，每个合法区间有两个状态：先手必败或先手必胜。对于所有\(l+r=k\)的区间的状态都是一样的，证明如下：

• \([l,r]\)为先手必败：
  则\([l-1,r],[l,r+1]\)为先手必胜，那么\([l-1,r+1]\)为先手必败，这个很简单
• \([l,r]\)为先手必胜，即\([l+1,r]\text{或}[l,r-1]\)为先手必败。
  • \([l+1,r]\)为先手必败，那么\([l+1,r+1]\)为先手必胜，那么可以推出\([l,r+1]\)为先手必败，(因为选\(l\)变成\([l+1,r+1]\)那样就是后手必胜即先手必败，选\(r+1\)同理)，所以\([l-1,r+1]\)就为先手必胜
  • \([l,r-1]\)为先手必败，同理

得证。
那么题目的问题就转化为了求\([1+d,n-d]\)的状态了(\(d\)为最大的，使得\([1+d,n-d]\)合法但是\([1+d+1,n-d-1]\)不合法了)可以二分得到\(d\)，那么当先手选了\(l\)，那么后手为了不输，就会选择\(l+1\)以此类推。先手选了\(r\)同理。于是我们需要找到最大的\(k\)使得\(a[1+d,1+d+k-1]\le s\)和\(a[n-d-k+1,n-d]\le s\)然后对\(k\)的奇偶性进行分讨即可，总复杂度就是\(O(n\log n)\)

10.22

P3177 [HAOI2015] 树上染色

题目就不多说了，\(dp\)方程也不解释了(比较简单),主要就是这道题的优化方式，
朴素的转移方程:

\[f_{i,j}=\max_{k=0,j}f_{i-1,j-k}+g_{i,k}\cdots \]

这个东西直接做是\(O(nk^2)\)的会炸，加优化，这个的加优化方式相当于剪枝了，详细如下：

因为这个题是向子树里放点，所以很显然，放的点的个数不能超过子树的总的点数。而上面的转移会出现放不下但还是放的问题，所以我们针对这一部分进行剪枝。答案就是将转移过程中的\(j,k\)都限制在子树大小内，这样就能近似\(O(nm)\)了。...很不对劲对但是跑的飞快

ll num = 0;
    for(int i = head[u]; i; i = edge[i].nxt) {
        int v = edge[i].to;
        if(v == fa) continue;
        num += siz[v];
        cnt ++;
        for(int j = 0; j <= num; j ++) g[cnt][j] = -1;
        for(ll j = 0; j <= min(k, num); j ++) {
            for(ll K = max(siz[v] - n + k - 1, 0ll); K <= min(j, siz[v]); K ++) {
                if(g[cnt - 1][j - K] == -1 || j - K > num - siz[v]) continue;
                ll val = (K * (k - K) + (siz[v] - K) * (n - k - siz[v] + K)) * edge[i].w;
                val += g[cnt - 1][j - K] + f[v][K];
                g[cnt][j] = max(g[cnt][j], val);
            }
        }
    }