0-n BFS总结

最近看到几个关于Dijkstra变形题，都是边权在限定范围内，用规则保证最小性，而不需要从优先队列中取。
例如：

• 0-1 BFS: 0-1 BFS (Shortest Path in a Binary Weight Graph)
• 1-2 BFS: https://codetop.cc/discuss/135
• 1-5 BFS: 【求助】如何用线性时间复杂度解决单源最短路径问题

参考 0-1 BFS [Tutorial] 里有一句最重要的话，

引理： “在 BFS 执行期间，持有顶点的队列仅包含来自 BFS 树的最多两个连续级别的元素。”

解释： 因为在执行 BFS 的每个点，我们只遍历到一个顶点的相邻顶点，因此队列中的每个顶点都与队列中的所有其他顶点最多相距一层。

推论：对于边权为0-n的图，BFS过程中，队列中元素的差值不会超过n

我们以0-2 BFS为例，可以用三层来表示BFS过程中的队列情况，利用三个数组滚动进行，可以O(1)入队，O(1)得到当前最小值

例如：

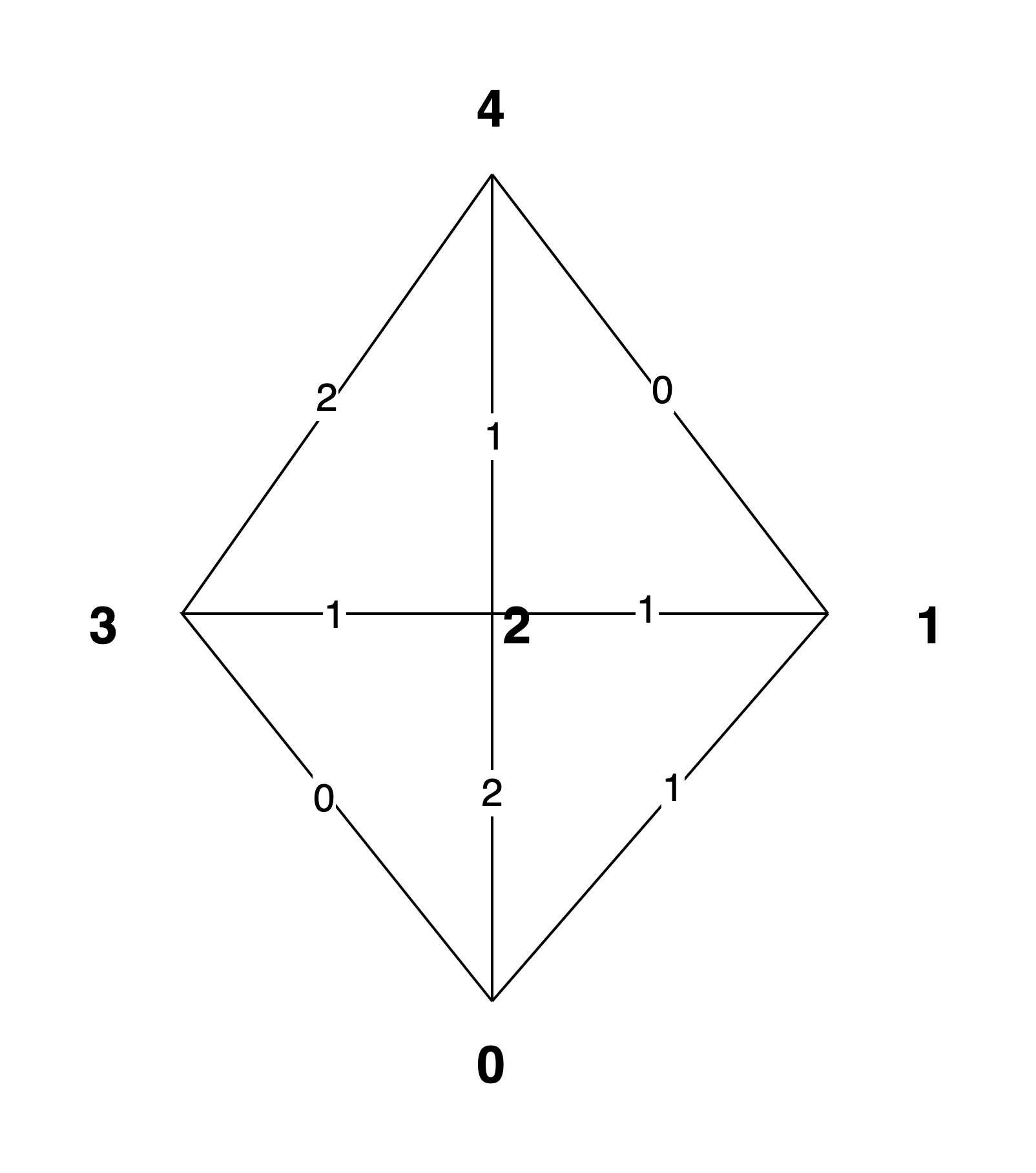
求节点0到其他节点的最短路
三层列表的更新过程如下：
首先0加入0号队列，并将更新的节点放入对应的队列...，cur号队列取完了就取cur+1号队列，直到三个队列都为空

0号队列	0	3
1号队列		1	1,2	2,4	4
2号队列		2	2,4	2,4	2,4	2,4	2,4	4

最终最短距离分别为：0 1 1 0 1

代码实现：
参考了 https://codetop.cc/discuss/135

#include<iostream>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;

const int V = 100000+5;

struct Node {
    int id, w;
    Node(int id_, int w_): id(id_), w(w_) {}
};

// 查看队列详情
// void print_que(const queue<int>& que_) {
//     queue<int> que = que_;
//     while (!que.empty()) {
//         cout << que.front() << " ";
//         que.pop();
//     }
//     cout << endl;
// }

vector<Node>edges[V];
queue<int> q[3];
void three_shortest_path(int n, int s, int t) {
    vector<int>dist(V, INT_MAX);
    dist[s] = 0;

    int cur = 0;
    q[cur].push(s);

    while(!(q[0].empty() && q[1].empty() && q[2].empty())) {

        // for(int i = 0;i < 3;i++) {
        //     cout << "i: " << i << endl;
        //     print_que(q[i]);
        // }

        if(!q[cur].empty()) {
            int u = q[cur].front();
            q[cur].pop();
            for(auto &e: edges[u]) {
                if(dist[e.id] > dist[u] + e.w) {
                    dist[e.id] = dist[u] + e.w;
                    q[(cur+e.w)%3].push(e.id);
                }
            }
        } else {
            cur = (cur+1)%3;
        }
       
    }
    for(int i = 0; i < n; i++) {  // 打印结果
        if(dist[i] == INT_MAX) {
            printf("-1\n");
        } else {
            printf("%d\n", dist[i]);
        }
    }
    // printf("%d\n", dist[t]);
}

int main() {
    int n, m, s, t;
    scanf("%d%d%d%d", &n, &m, &s, &t);
    for(int i = 0; i < m; i++) {
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        edges[u].push_back(Node(v, w));
        edges[v].push_back(Node(u, w));
    }
    three_shortest_path(n, s, t);
    return 0;
}