编程之美阅读笔记
1. 判断一个点是否在三角形内部
常用的tirck：计算三部分面积和，由于浮点数有精度问题，可能会出错
还有其他方法吗？？
可以利用叉乘
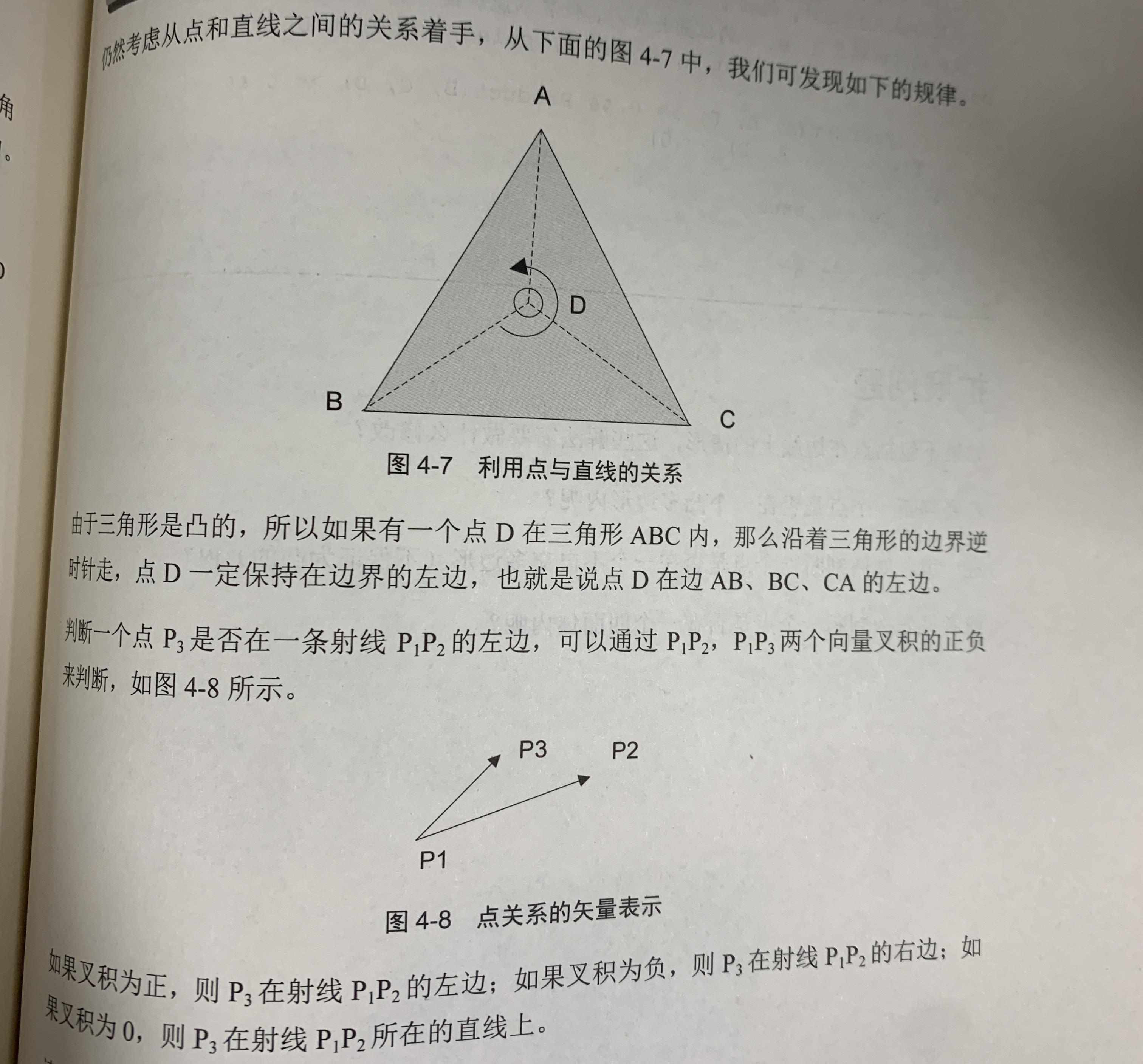
如果在三角形内部，沿着边逆时针走，D一定都是在左边；或者顺时针走，D一定都在右边
而判断点在线的左边还是右边 可以用叉乘
点击查看代码
#include<iostream>
using namespace std;
struct Point
{
int x;
int y;
Point(int x, int y) : x(x), y(y) {}
};
// Function to find orientation of ordered triplet (p, q, r).
// p1p2 x p1p3
int CrossProduct(Point p1, Point p2, Point p3)
{
return (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x);
}
int PointInTriangle(Point p, Point p1, Point p2, Point p3)
{
// Find orientation
int o1 = CrossProduct(p1, p2, p);
int o2 = CrossProduct(p2, p3, p);
int o3 = CrossProduct(p3, p1, p);
// If p is colinear with at least 2 points, then check if it lies
// in the triangle or not
if (o1 == 0 && o2 == 0 && o3 == 0)
{
if (p.x <= max(p1.x, max(p2.x, p3.x)) && p.x >= min(p1.x, min(p2.x, p3.x)) &&
p.y <= max(p1.y, max(p2.y, p3.y)) && p.y >= min(p1.y, min(p2.y, p3.y)))
return 1;
else
return 0;
}
// Check if p is in triangle or not
return (o1 >= 0 && o2 >= 0 && o3 >= 0) || (o1 <= 0 && o2 <= 0 && o3 <= 0);
}
int main() {
Point p1(0, 0), p2(10, 0), p3(5,8);
Point d(-1,0);
if(PointInTriangle(d, p1, p2, p3))
cout << "The point is inside the triangle";
else
cout << "The point is outside the triangle";
return 0;
}
2. 将一个数组分成两个等长的子数组，要求两者的和尽可能接近
看似简单，实则是近期遇到的思考最久的了
例如，我们可以暴搜得到k个，更新最接近的值，复杂度 \(n^{n/2}\)
仔细想，这是一个背包问题，2n个物品，选取n个，使得值尽可能接近一半
通常背包问题中 dp[i][j] 表示前i个物品体积为j时的 最大价值/能够装下，但是这没有保证物品的个数
加入我们定义bool dp[i][j] 为 i个物品 sum为j 是否可能，依次考虑每个物品的贡献，当第 k 个物品时，对之前每一行都要更新，例如根据第二行(也就是只有2个物品)，更新第三行(表示物品数目为3)
与普通的背包相比，之前的每一行都是有用的，而普通背包只用了前一行，通常可以用滚动数组省掉
点击查看代码
void canPartitionLike(vector<int>& nums) {
int sum = 0, n = nums.size();
for(int num : nums) sum += num;
bool dp[n+1][sum/2+1];
memset(dp, 0, sizeof(dp));
cout << "dp...." << endl;
// for(int i = 0; i <= n; i++) dp[i][0] = true;
dp[0][0] = true;
for(int i = 1; i <= n; i++) { // 依次考虑每个物品
for(int j = 1; j <= sum/2; j++) { // 每个和
for(int k = i; k > 0; k--) { // 每一行
if(j >= nums[i-1] && dp[k-1][j-nums[i-1]])
dp[k][j] = true;
}
}
}
cout << "****" << endl;
for(int i = 0; i <= n; i++) {
for(int j = 0; j <= sum/2; j++) {
cout << dp[i][j] << " ";
}
cout << endl;
}
for(int i = sum/2; i >= 0; i--) {
if(dp[n/2][i]) {
cout << i << endl;
break;
}
}
}
3. 将数组循环右移 k 位
例如 abcd1234
右移1位：4abcd123
右移2位：34abcd12
右移3位：234abcd1
可以发现规律，虽然右移了，但是右移结果都可以划分成原来顺序两段，例如 34 abcd12
所以，可以先划分，再整体翻转，再部分翻转
点击查看代码
void Reverse(vector<int>& nums, int start, int end) {
while (start < end) {
swap(nums[start], nums[end]);
start++;
end--;
}
}
vector<int> RightShiftK3(vector<int>& nums, int k) {
Reverse(nums, 0, nums.size() - 1);
Reverse(nums, 0, k - 1);
Reverse(nums, k, nums.size() - 1);
return nums;
}
4. 子数组的最大乘积
给定一个长度为N的数组，不允许用除法，计算任意N-1个元素的最大乘积
解法：
解法一：枚举所有组合n * 每个组合计算乘积 n，复杂度\(O(n^2)\)
解法二：枚举不乘的元素，将左右两边的乘积相乘，前缀和后缀可以预处理，复杂度\(O(n)\)
解法三：分类讨论
5. 不要被阶乘吓倒
问题1：求 N! 末尾有多少个0？
问题2：求 N! 的二进制表示中最低位1的位置
问题1的解法：就是1~n中"5"的出现次数，因为"2"肯定比5多
res = N/5 + N/25 + N/125...
问题2的解法：最低位1的位置就是"2"的次数
而"2"的次数等于 N/2 + N/4 + N/8...
6. 判断链表是否相交
解法一：连接成环，将A的尾接到B的头，再从A或B出发
加入限定是"Y"型
可以用解法二：A、B都走到最末尾，判断两个末尾节点是否相同
