心得：刷算法的痛点-只根据题目的case思考，不考虑边界情况，写出一坨shit

977. 有序数组的平方
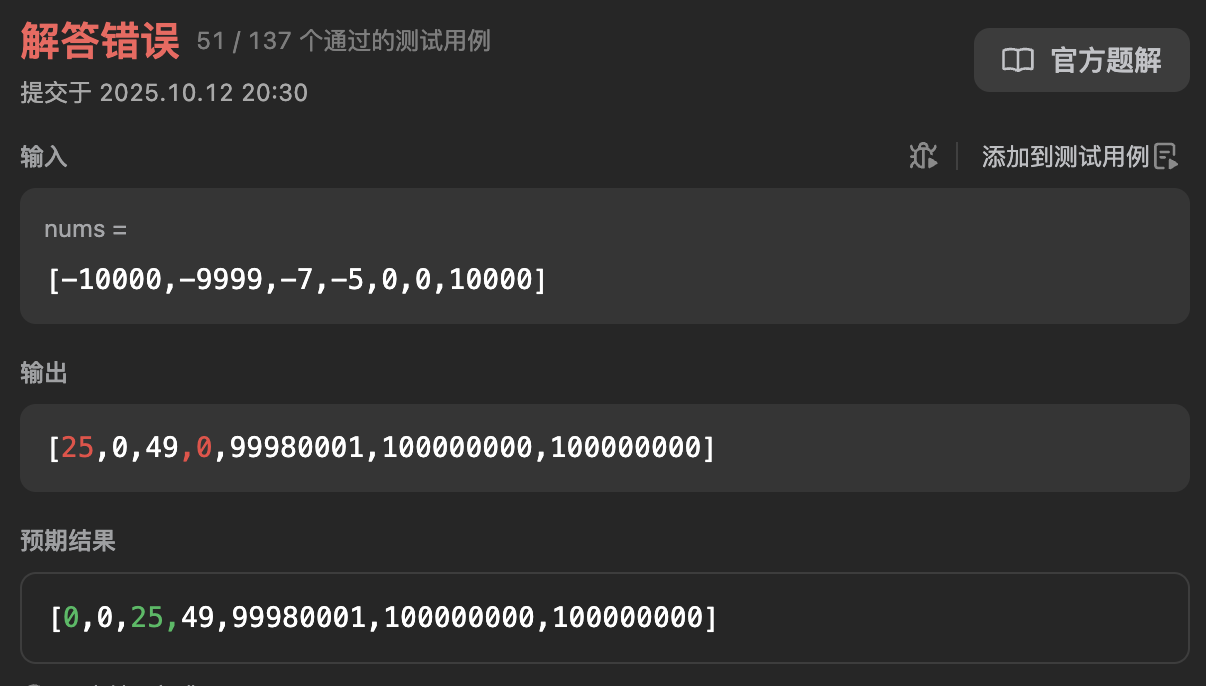
不停地根据错误用例给代码打补丁，最后还是会有新的错误用例，永远补不好。
下面展示一下耗时1小时产出的💩

class Solution {
    public int[] sortedSquares(int[] nums) {
        // 统计nums数组中非正数的个数
        int count = 0; // 非正数的个数
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] < 0) {
                count++;
            }
        }

        int left = 0;
        int right = nums.length - 1;
        int[] ans = new int[nums.length];

        // 对每个元素平方
        for (int i = 0; i < nums.length; i++) {
            nums[i] = nums[i] * nums [i];
            ans[i] = nums[i];
        }

        // 1、nums中没有正数，平方后非递增
        if (count == nums.length) {
            int j = nums.length - 1;
            for (int i = 0; i < nums.length; i++) {
                ans[j--] = nums[i];
            }
            return ans;
        }

        //2、nums中都是正数，平方后依旧非递减
        if (count == 0) return ans;

        // 3、nums中第一个元素为0，其余为正数,平方后依旧非递减
        if (count == 1 && nums[0] == 0) return ans;

        // 4、nums中有正有负
        // 未排序的元素中，最大值在 left 与 right 之间
        int tmp = 0;
        int n = nums.length - 1;
        while (left <= right) {
            // 只剩最后一个元素未排序
            if (left == right) {
                ans[n] = nums[left];
                break;
            }
            // 将 left 与 right 所指元素添加到新数组 ans中
            if (nums[left] > nums[right]) {
                ans[n--] = nums[left];
                ans[n--] = nums[right];
            } else {
                ans[n--] = nums[right];
                ans[n--] = nums[left];
            }
            // 更新待排序元素的区间
            left++;
            right--;
        }
        return ans;
    }
}