高斯消元学习笔记——P304题解

如果你觉得这篇太啰嗦

问题

[SDOI2006] 线性方程组

题目描述

已知 \(n\) 元线性一次方程组。

\[\begin{cases} a_{1, 1} x_1 + a_{1, 2} x_2 + \cdots + a_{1, n} x_n = b_1 \\ a_{2, 1} x_1 + a_{2, 2} x_2 + \cdots + a_{2, n} x_n = b_2 \\ \cdots \\ a_{n,1} x_1 + a_{n, 2} x_2 + \cdots + a_{n, n} x_n = b_n \end{cases} \]

请根据输入的数据，编程输出方程组的解的情况。

---

题解

打眼一看，这不是大版汁嘛😎。立刻把这个题的代码直接提交：

#include<bits/stdc++.h>
using namespace std;
double mapp[110][110],ans[110];
int n;
int main(){
	cin>>n;
	int r;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n+1;j++){
			cin>>mapp[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		r=i;
		for(int j=i;j<=n;j++){
			if(fabs(mapp[r][i])<fabs(mapp[j][i])){
				r=j;
			}
		}
		if(fabs(mapp[r][i])<1e-7){
			cout<<"No Solution"<<endl;
			return 0;
		}
		swap(mapp[i],mapp[r]);
		double t=mapp[i][i];
		for(int j=i;j<=n+1;j++){
			mapp[i][j]/=t;
		}
		for(int j=i+1;j<=n;j++){
			t=mapp[j][i];
			for(int k=i;k<=n+1;k++){
				mapp[j][k]-=mapp[i][k]*t;
			}
		}
	}
	ans[n]=mapp[n][n+1];
	for(int i=n-1;i>=1;i--){
		ans[i]=mapp[i][n+1];
		for(int j=i+1;j<=n;j++){
			ans[i]-=mapp[i][j]*ans[j];
		}
	}
	for(int i=1;i<=n;i++){
		printf("x%d=%.2lf\n",i,ans[i]);
	}
}

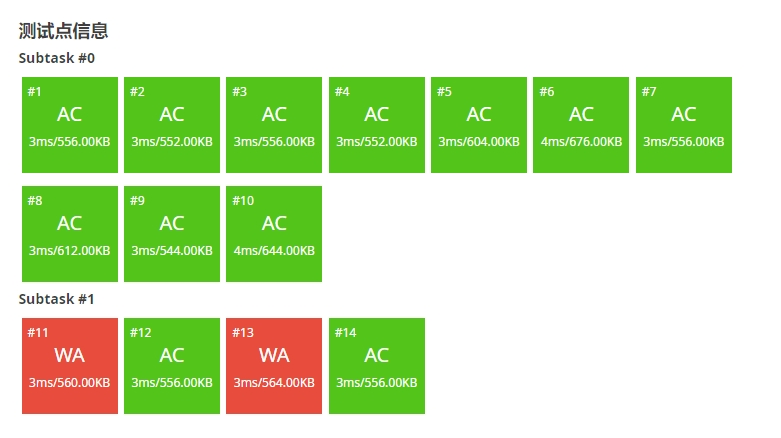
o,我没有仔细读题，还要再判断是无解还是无穷解。

😕看来并没有那么简单，但注意到，可以通过一个计数器来记录是什么时候break掉的，如果计数器不等于n，就要进行判断：

if(t!=n){
	if(mapp[t][n+1]){
		cout<<-1;
		return 0;
	}
	else{
		cout<<0;
		return 0;
	}
}

那么加上优化，我们的代码变成了几分呢？

🤡这不纯纯消愁嘛

经过一番排查，发现了一个显而易见的问题：要一层层的排查t以后的层数（除了我这个蒟蒻都能看出来吧）

if(t<n){
	while(t<n){
		if(mapp[t++][n]<1e-7){
			cout<<-1;
			return 0;
		}
	}
	cout<<0;
	return 0;
}

这个优化立竿见影！

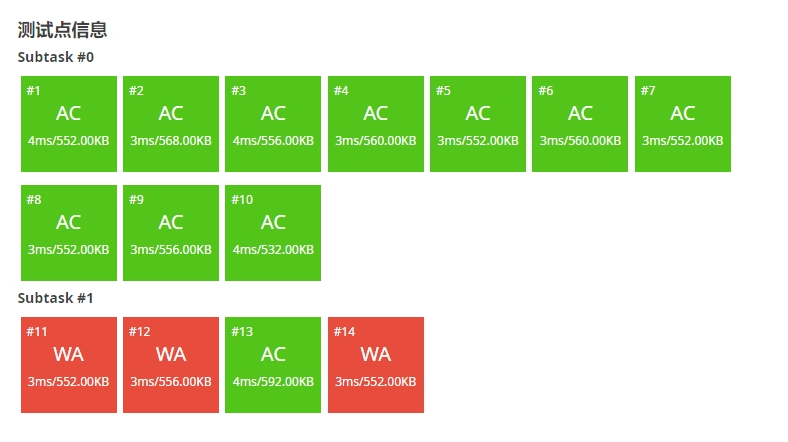
🎉️耶！

但有些聪明的人肯定已经发现了问题：测试点12本来是A的，但加上优化就戳了：（

但是愚蠢的LEWIAK并没有发现，拿着错误代码调了114分钟

这时，我灵机一动💡，想直接返璞归真暴力判断是否为完美梯形：

if(tt<n){
    for(int i=1;i<=n;i++){
		for(int j=i;j<=n;j++){
			if(!mapp[i][j]){
				if(mapp[i][n+1]){
					cout<<-1;
					return 0;
				}
			}
		}
	}
    cout<<0;
	return 0;
}

那么返璞归真后，我们的代码变成了几分呢？

🤡

还有翻转！

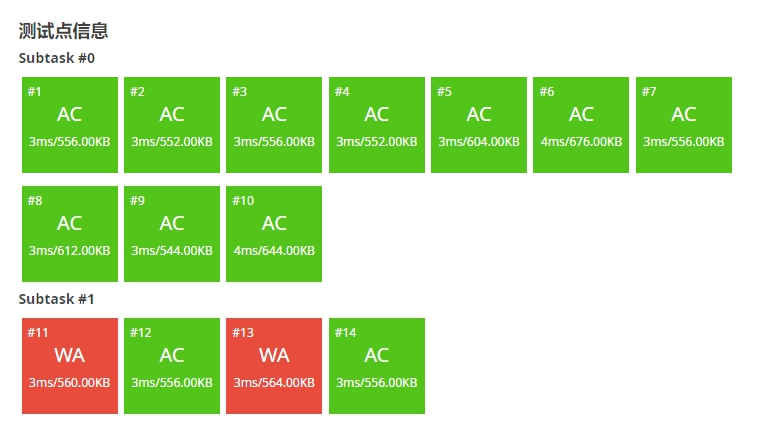
但有些聪明的人肯定已经发现了问题：测试点12本来是A的，但加上优化就戳了：（

的原因其实是：

变量名冲突

最离谱的是我的婢养的DEV C++竟然没有检查出错（不是哥们，他一个int一个double都不报错的吗？）

😁很有希望！

但是愚蠢的LEWIAK调了半天后发现了严重的问题

那就是我们的代码实际上并没有处理完成所有的消元👀️

倒是也好处理😎，把break换为continue就好了。

🤓🤓🤓

想了想发现：应该把i换成tt，因为有一些是不算的：

（懒得贴了，自己想象WA的评测信息吧）

🤓🤓🤓

经过苦思冥想，我发现要用别的多项式消掉continue的，而为了节省空间，我决定无脑的将从i到n的循环改为从1到n的循环

其实LEWISAK只是懒的用数组单独存储罢了

最后贴上ACcode：

#include<bits/stdc++.h>
using namespace std;
double mapp[110][110],ans[110];
int tt=0;
int n;
int main(){
	cin>>n;
	int r;
	for(int i=0;i<n;i++){
		for(int j=0;j<n+1;j++){
			cin>>mapp[i][j];
		}
	}
	for(int i=0;i<n;i++){
		r=tt;
		for(int j=tt+1;j<n;j++){
			if(fabs(mapp[r][i])<fabs(mapp[j][i])){
				r=j;
			}
		}
		if(fabs(mapp[r][i])<1e-9){
			continue;
		}
		for(int j=0;j<n+1;++j)swap(mapp[tt][j],mapp[r][j]);
		double t;
		for(int j=0;j<n;j++){
			if(j==tt){
				continue;
			}
			t=mapp[j][i]/mapp[tt][i];
			for(int k=i;k<n+1;k++){
				mapp[j][k]-=mapp[tt][k]*t;
			}
		}tt++;
	}
	if(tt<n){
		while(tt<n){
			if(fabs(mapp[tt++][n])>=1e-9){
				cout<<-1;
				return 0;
			}
		}
		cout<<0;
		return 0;
	}
	
	for(int i=0;i<n;i++){
		printf("x%d=%.2lf\n",i,mapp[i][n]/mapp[i][i]);
	}
}

改马蜂是因为玄学

小彩蛋：