伏羲六十四卦 -(仿射密码)

题目：

这是什么，怎么看起来像是再算64卦！！！

密文:升随临损巽睽颐萃小过讼艮颐小过震蛊屯未济中孚艮困恒晋升损蛊萃蛊未济巽解艮贲未济观豫损蛊晋噬嗑晋旅解大畜困未济随蒙升解睽未济井困未济旅萃未济震蒙未济师涣归妹大有

嗯？为什么还有个b呢?
b=7


flag：请按照格式BJD{}

# -- coding:UTF-8 --
from secret import flag

def encrpyt5():
    enc=''
    for i in flag:
        enc+=chr((a*(ord(i)-97)+b)%26+97)
    return(enc)

def encrypt4():
    temp=''
    offset=5
    for i in range(len(enc)):
        temp+=chr(ord(enc[i])-offset-i)
    return(temp)

首先了解一下：
仿射密码（Affine Cipher）是一种单表代换密码，它是线性变换的一种应用，常用于信息加密。下面为你介绍其加密和解密公式。
加密公式
仿射密码的加密函数是一个线性函数，假设明文字母表大小为 m（例如在英文字母表中，不区分大小写时 m=26），对于明文中的每个字母 x（x 的取值范围是 0 到 m-1），其对应的密文 y 可以通过以下公式计算：
y=(ax+b) mod m
其中：
a 和 b 是密钥的组成部分，a 必须与 m 互质（即 gcd(a,m)=1），这是为了保证加密函数是一个双射函数，从而确保可以正确解密。
b 是一个整数，取值范围是 0≤b<m。
\(\bmod\) 是取模运算符，用于确保结果在 0 到 m-1 的范围内。
解密公式
为了解密密文 y 得到明文 x，需要先找到 a 在模 m 下的乘法逆元 a^(-1)，即满足 (a×a^(-1) )≡1 (mod m) 的整数 a^(-1)。然后使用以下公式进行解密：
x=a^(-1) (y-b) mod m
其中 a^(-1) 是 a 在模 m 下的乘法逆元，可通过扩展欧几里得算法来计算。
示例
假设使用英文字母表（m=26），选择 a=5（因为 gcd(5,26)=1）和 b=8 作为密钥。
加密：如果要加密字母 'C'，在字母表中 'C' 对应的数字是 x=2（'A' 对应 0，'B' 对应 1，以此类推）。将 a=5，b=8，x=2 代入加密公式 y=(ax+b) mod m，得到 y=(5×2+8) mod 26=(10+8) mod 26=18，对应字母表中的 'S'。
解密：首先需要计算 a=5 在模 26 下的乘法逆元 a^(-1)。通过扩展欧几里得算法可计算出 a^(-1)=21，因为 (5×21) mod 26=1。如果密文是 'S'，对应数字 y=18，将 a^(-1)=21，b=8，y=18 代入解密公式 x=a^(-1) (y-b) mod m，得到 x=21×(18-8) mod 26=21×10 mod 26=210 mod 26=2，对应字母表中的 'C'。

解题：
64卦 => base64 => b=7 => 逆向jm4 => 逆向jm5 => 爆破a => 仿射密码 => flag

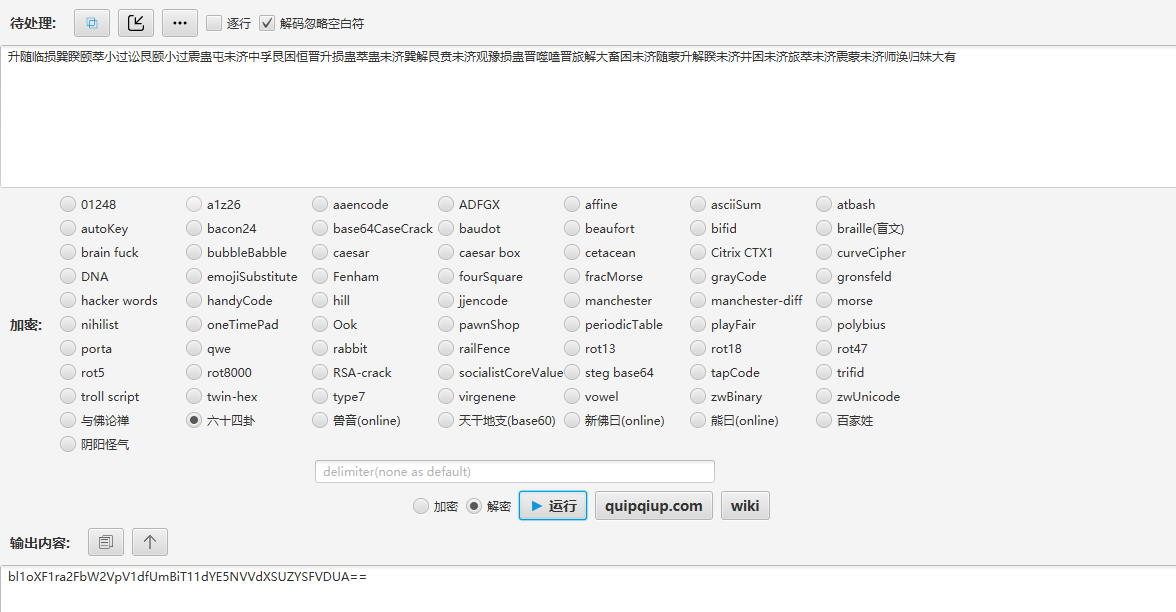
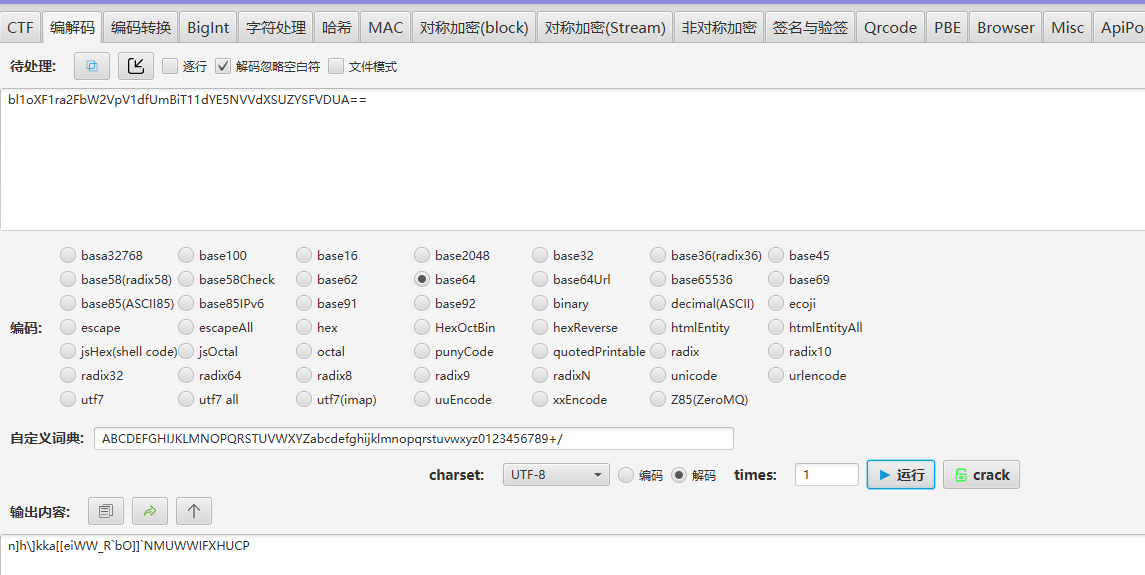
脚本：

import gmpy2
str = 'n]h\\]kka[[eiWW_R`bO]]`NMUWWIFXHUCP'
print(str)
def jm4(t):
    zfc = ''
    for i in range(len(t)):
        zfc +=  chr(ord(str[i])+5+i)
    return(zfc)
def jm5(z):
    zfc = ''
    flag = ''
    for a in range(100):
        for i in range(len(z)):
        #enc+=chr((a*(ord(i)-97)+b)%26+97)
            zfc = ord(z[i])-97
        # zfc = (a*x+b)%y
            try:
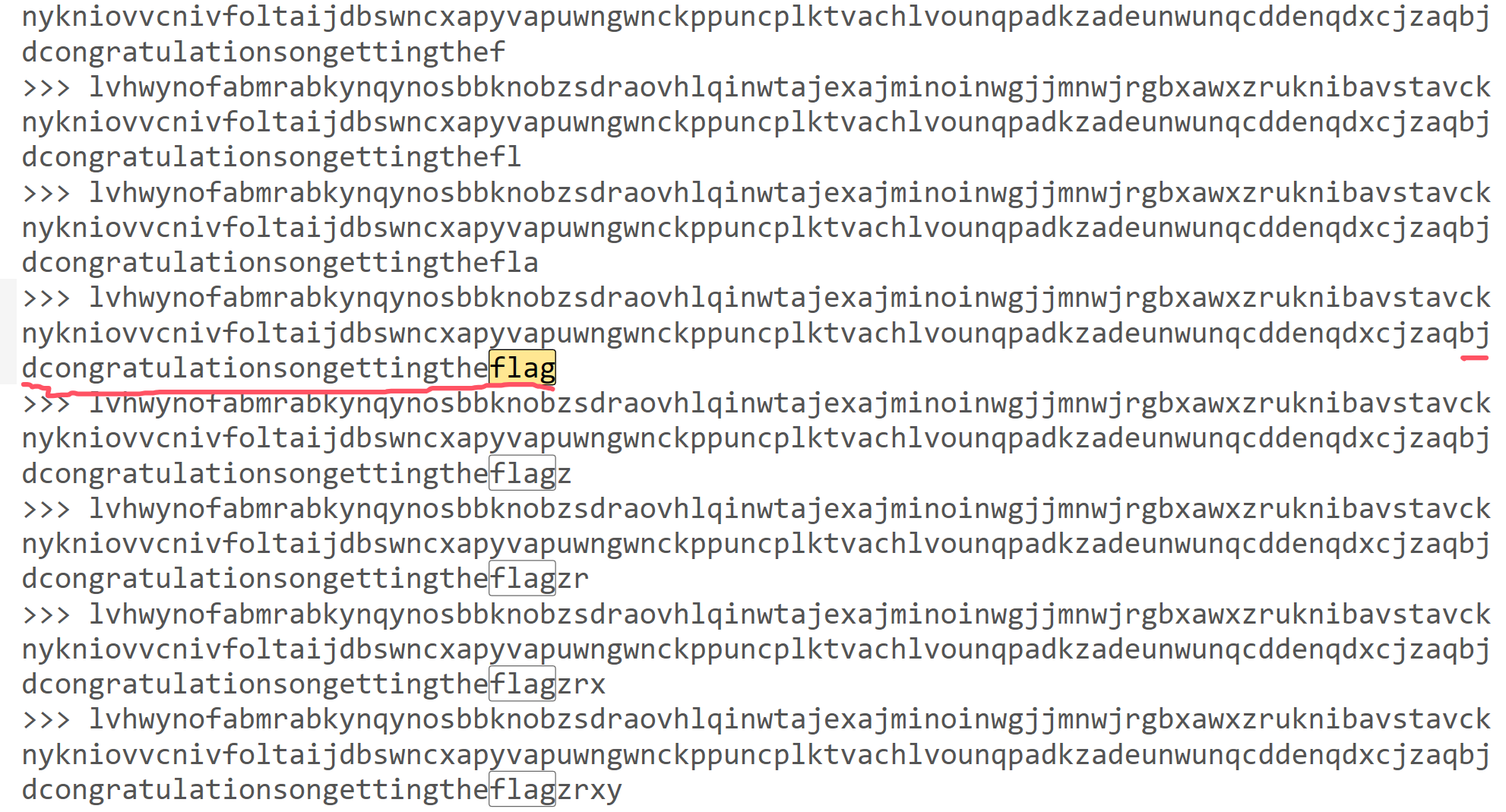
                flag  += chr(gmpy2.invert(a,26)*(zfc-7)%26+97)
                print(">>>",flag)
            except:
                pass

flag = jm4(str)
print(flag)
flag_ = jm5(flag)