电子科技大学研究生试卷
课程名称 图论及其应用
教师 学时 60 学分 3
教学方式 堂上授课
考核日期 2017年_6月11日
一．填空题(每空5分，共25分)
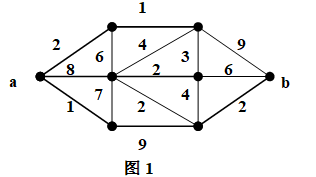
1.图1中顶点a到顶点b的距离d（a，b）=________________________(11)
2.已知图G的邻接矩阵
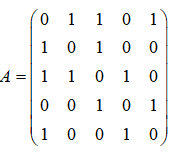
，则G中长度为2的途径总条数为____________。(30)
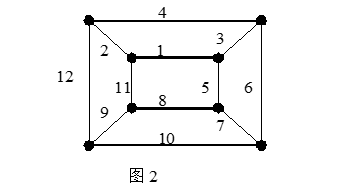
3.图2中最小生成树T的权值W（T）=________________。(34)
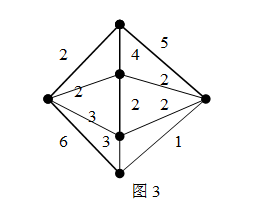
4.图3的最优欧拉环游的权值为_____________.（38）
5.树叶带权分别为1，2，4，5，6，8的最优二元树权值为w（T）=______________________。（62）
二．单项选择(每题3分，共15分)
1，关于图的度序列，下列说法正确的是（）.（C）
（A）对任意一个非负整数序列来说，它都是某图的度序列；
（B）如果非负整数序列\(\pi=(d_1,d_2,...,d_n)\)满足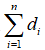
为偶数，则它一定是图序列；
（C）若图G度弱于图H，则图G的边数小于等于图H的边数；
（D）.如果图G的顶点总度数大于或等于图H的顶点总度数，则图G度优于图H。
2，关于图的割点与割边，下列说法正确的是（）.D
（A）有割边的图一定有割点；
（B）有割点的图一定有割边；
（C）有割边的简单图一定有割点；
（D）割边不在图的任一圈中。
3设\(k(G),\lambda(G),\delta(G)\)分别表示图G的点连通度，边连通度和最小度。下面说法错误的是（）D
（A）存在图G，使得\(k(G)=\lambda(G)=\delta(G)\)
（B）存在图G，使得\(k(G)<\lambda(G)<\delta(G)\)
（C）设G是n阶简单图，若
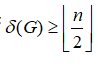
,则G连通，且\(\lambda(G)=\delta(G)\).
（D）图G是k连通的，则G的连通度为k。
4.关于哈密尔顿图，下列命题错误的是( )B
(A) 彼得森图是非哈密尔顿图；
(B) 若图G的闭包是哈密尔顿图，则其闭包一定是完全图；
(C) 若图G的闭包是完全图，则图G是哈密尔顿图；
(D) 设G是三阶以上简单图，若G中任意两个不邻接点u与v，满足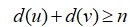
，则G是哈密尔顿图。
5.下列说法错误的是( )A
(A) 有完美匹配的三正则图一定没有割边；
(B) 没有割边的三正则图一定存在完美匹配；
(C) 任意一个具有哈密尔顿圈的三正则图可以1因子分解；
(D) 完全图\(K_{2n+1}\)是n个哈密尔顿圈的和。
三、 (10分) 设无向图G有10条边，3度与4度顶点各2个，其余顶点的度数均小于3，问G中至少有几个顶点？在最少顶点数的情况下，写出G的度序列，该度序列是一个图序列吗？。
解：要使得G中顶点数最少，度数小于3的顶点度数必须取2.
设度数为2的顶点个数为\(x\)，由握手定理：
\(3\times2+4\times2+2x=20\)，解得：\(x=3\)
所以，G中至少顶点个数为7.
G的度序列\(\pi=(4,4,3,3,2,2,2)\)
由于\(\pi_1=(3,2,2,2,2,1),\pi_2=(2,1,1,1,1)\)
所以，度序列为图序列。
四、 (6分) 求完全图\(K_n\)的邻接谱。
解：完全图\(K_n\)的邻接矩阵为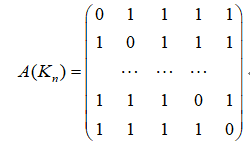
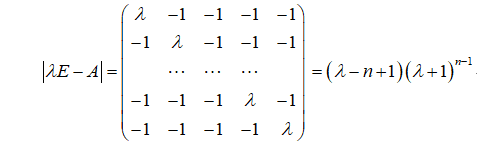
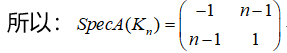
五，(6分) 求证：一棵非平凡树至少有两片树叶。
证明 设P=v1v2…vk是非平凡树T中一条最长路，则v1与vk在T中的邻接点只能有一个，否则，要么推出P不是最长路，要么推出T中存在圈，这都是矛盾！即说明v1与v2是树叶。
六，(6分) 求证对于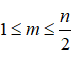
的图
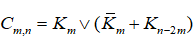是非哈密尔顿图。
证明：取S=V(km),则ω(G-S)=m+1>|S|=m,所以，由H图的性质知，G是非H图。
七.(6分)求证：设\(l\)是赋权完全偶图G的可行顶点标号，如果其相等子图存\(G_l\)在完美匹配\(M^*\)，则\(M^*\)是G的最优匹配。
证明：设M*是\(G_l\)的完美匹配，则：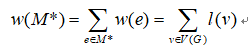
又设M是G的任一完美匹配，则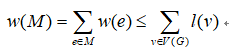
所以，w (M*)≥w (M)。即M*是G的最优匹配。
八.(6分) 设简单可平面图G有10个4度顶点和8个5度顶点，其余顶点度数均为7。求7度顶点的最大可能数量。
解:设7度顶点有\(x\)个。
一方面，由握手定理：\(4\times10+5\times8+7x=2m\)
即：\(m=40+3.5x\)
另一方面：由于图G是可平面简单图，因此：\(m\leq3n-6=3(10+8+x)-6=48+3x\)
解得：\(x\leq16\)
即7度顶点的最大可能数量为16.
九．(10分)求下图G的色多项式\(p_k(G)\).并求出点色数。
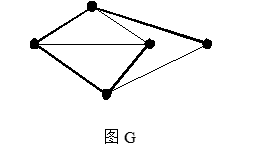
解：做出\(\overline G\):
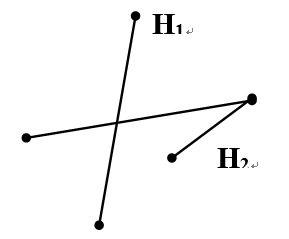
\(p_k(G)=(x+x^2)(2x^2+x^3)=x^5+2x^4+2x^3=k(k-1)(k-2)(k-3)(k-4)+2k(k-1)(k-2)(k-3)+2k(k-1)(k-2)\)
\(p_1(G)=0,p_2(G)=0,p_3(G)=12\)
所以点色数为3
十.(10分) 一家公司计划建造一个动物园，他们打算饲养下面这些动物：狒狒(b)、狐狸(f)、山羊(g)、土狼(h)、非洲大羚羊(k)、狮子(l)、豪猪(p)、兔子(r)、鼩鼱(s)、羚羊(w)和斑马(z)。根据经验，动物的饮食习惯为：狒狒喜欢吃山羊、非洲大羚羊、兔子和鼩鼱；狐狸喜欢吃山羊、豪猪、兔子和鼩鼱；土狼喜欢吃山羊、非洲大羚羊、羚羊和斑马；狮子喜欢吃山羊、非洲大羚羊、羚羊和斑马；豪猪喜欢吃鼩鼱和兔子；而其余的则喜欢吃虫子、蚯蚓、草或其它植物。公司将饲养这些动物，希望它们能自由活动但不能相互捕食。求这些动物的一个分组，使得需要的围栏数最少。(要求用图论方法求解)
解：每个动物作为顶点，如果动物x要吃y，则该两点连线。
问题转化为：(1)在模型图中求出其点色数\(\chi(G)\)；(2)用\(\chi(G)\)种颜色对图G进行正常顶点作色。则色组即为动物分组。
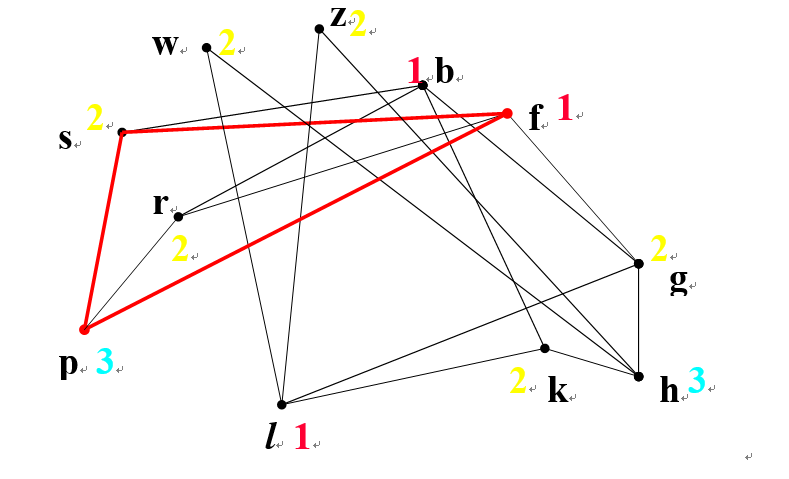
由于在模型图中存在三角形fsp，所以\(\chi(G)\geq3\)，另一方面，用三种颜色可实现对图G的正常点作色，得到\(\chi(G)\leq3\)。所以，点色数\(\chi(G)=3\)。
给出的围栏分组为：\(\{b,f,l\};\{g,k,r,s,w,z\};\{h,p\}\)
posted on
