第四章 欧拉图与哈密尔顿图
(一)、欧拉图及其性质
(1)、问题背景---欧拉与哥尼斯堡七桥问题
问题：对于图G，它在什么条件下满足从某点出发，经过每条边一次且仅一次，可以回到出发点？
注：一笔画----中国古老的民间游戏（存在欧拉迹）
要求：对于一个图G, 笔不离纸, 一笔画成.
拓展：三笔画：在原图上添加三笔，可使其变为欧拉图。
定义1 对于连通图G，如果G中存在经过每条边的闭迹，则称G为欧拉图，简称G为E图。欧拉闭迹又称为欧拉环游，或欧拉回路。
定理1 下列陈述对于非平凡连通图G是等价的：
(1) G是欧拉图；
(2) G的顶点度数为偶数；
(3) G的边集合能划分为圈。
推论1 连通图G是欧拉图当且仅当G的顶点度数为偶。
推论2 连通非欧拉图G存在欧拉迹当且仅当G中只有两个顶点度数为奇数。
证明：若G和H是欧拉图，则\(G\times H\)是欧拉图。
若G是非平凡的欧拉图，则G的每个块也是欧拉图。
(二)、Fleury算法(欧拉图中求出一条具体欧拉环游的方法)
方法是尽可能避割边行走
(三)、中国邮路问题（最优欧拉环游，管梅谷）
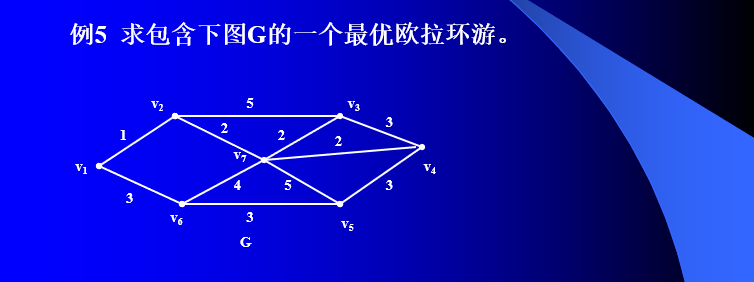
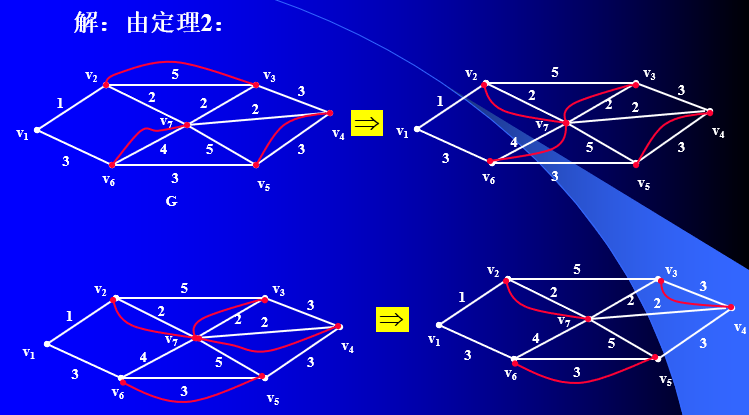
定理2 若W是包含图G的每条边至少一次的闭途径，则W具有最小权值当且仅当下列两个条件被满足：
(1) G的每条边在W中最多重复一次；
(2) 对于G的每个圈上的边来说，在W中重复的边的总权值不超过该圈非重复边总权值。
(四)、哈密尔顿图的概念
定义1 ： 如果经过图G的每个顶点恰好一次后能够回到出发点，称这样的图为哈密尔顿图，简称H图。所经过的闭途径是G的一个生成圈，称为G的哈密尔顿圈。
定义2: 如果存在经过G的每个顶点恰好一次的路，称该路为G的哈密尔顿路，简称H路。
(五)、哈密尔顿图性质与判定
1、性质定理【必要条件】；
定理1 (必要条件) 若G为H图，则对V(G)的任一非空顶点子集S，有：
注：不等式为G是H图的必要条件，即不等式不满足时，可断定对应图是非H、图。满足定理1不等式的图不一定是H图。
著名的彼德森图是非H图
若连通图G不是2-连通的，则G不是哈密尔顿图
2、狄拉克定理【充分条件】；
定理2 (充分条件) 对于n≧3的单图G，如果G中有： \(\delta(G) \geq \frac{n}{2}\) ,则G是H图.
3、奥尔定理【充分条件】；
定理3 (充分条件) 对于n≧3的单图G，如果G中的任意两个不相邻顶点u与v，有：
那么，G是H图。
4、邦迪定理（闭包定理）【充分必要条件】；
定义3 在n阶单图中，若对d (u) + d (v) ≧n 的任意一对顶点u与v，均有u adj v , 则称G是闭图。
引理1 若G1和G2是同一个点集V的两个闭图，则G = G1∩G2是闭图。
注：G1与G2都是闭图，它们的并不一定是闭图。
定义4 如果\(\overline{G}\)是包含G的极小闭图，则其是图G的闭包
图的闭包的构造方法：将图中度数之和至少是图的顶点个数的非邻接顶点对递归地连接起来，直到不再有这样的顶点对存在时为止。
引理2 图G的闭包是唯一的
引理3 对于单图G，如果G中有两个不相邻顶点u与v，满足：
那么G是H图当且仅当G + uv是H图 。
定理4(帮迪——闭包定理) 图G是H图当且仅当它的闭包是H图。【引理3证】
说明：1、对于一个具体的图，我们可以作出其闭包，若能够断定闭包是H图，则原图为H图。否则，定理失效！【太麻烦】
2、如果对满足一定条件的图G，能够从逻辑上说明其闭包是H图，则可以断定G是H图【掌握一点，看下面的例子】。
推论1：设G是n≧3的单图，若G的闭包是完全图，则G是H图。
5、邦迪-沙瓦达定理（度序列判定法）【充分条件】。
定理5(Chvátal——度序列判定法) 设简单图G的度序列是(d1,d2,…,dn), 这里，d1≦d2≦…≦dn,并且n≧3.若对任意的m<n/2,或有 dm>m,或有dn-m ≧ n-m,则G是H图。【可以证明，满足条件的图的闭包是完全图】
6、 范定理
若连通图中每对距离为2的点中有一点的度数至少是图的点数的一半，则该图是哈密尔顿图。
7、边数判定法
设G是n阶简单图。若n≥3且\(|E(G)>\left( \matrix{{n-1}\\2}\right)+1\)则G是H图；并且具有n个顶点条\(\left( \matrix{{n-1}\\ 2} \right)+1\)边的非H图只有\(C_{1,n}\)以及\(C_{2,5}\)
(六)、非哈密尔顿图与TSP问题
一、非哈密尔顿图特征
定义1 图G称为度极大非H图，如果它的度不弱于其它非H图。
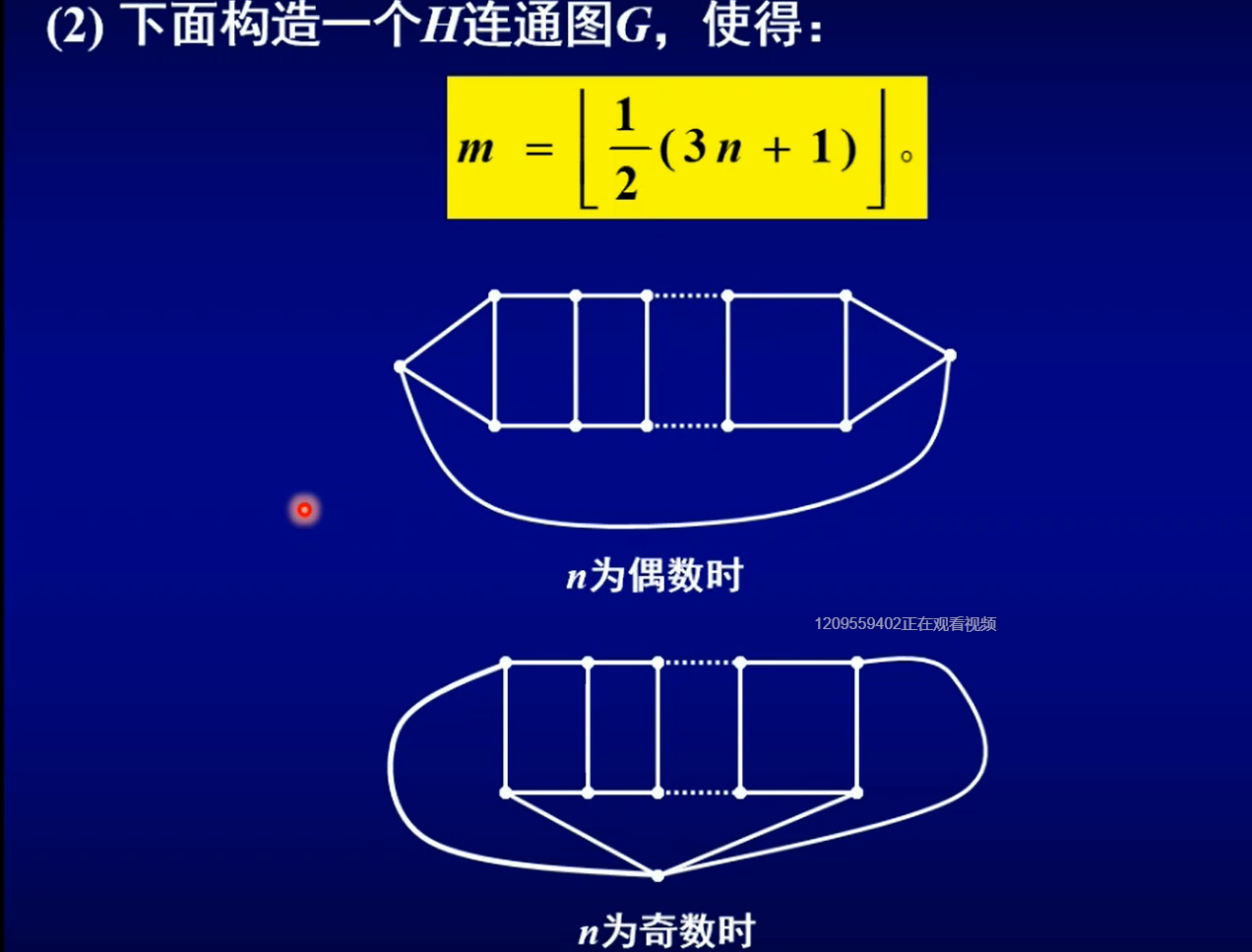
定义2 对于\(1\leq m \leq \frac{n}{2}\), \(C_{m,n}\) 图定义为：
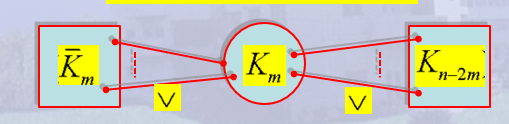
引理1 对于\(1\leq m \leq \frac{n}{2}\), \(C_{m,n}\) 图是非H图。
定理1 (Chvátal,1972) 若G是n≧3的非H单图，则G度弱于某个\(C_{m,n}\)图。(性质)
注： (1) 定理1刻画了非H单图的特征：从度序列角度看，\(C_{m,n}\) 图族中某个图是某个n阶非H单图的极图。
(2) \(C_{m,n}\) 图族中的图是度极大非哈密尔顿简单图。
(3) 定理1的逆不能成立！但有结论：n(≥3)阶单图若度优于C m, n 图族中所有图，则G是H图。
推论（边数判定法！） 设G是n阶单图。若n≧3且\(|E(G)> \left( \begin{array}{c} {n-1} \\2 \end{array} \right)+1|\)，则G是H图。并且，具有n个顶点 \(\left( \matrix{{n-1}\\2}\right)+1\) 条边的非H图只有\(C_{1,n}\)以及\(C_{2,5}\).
二、TSP问题(旅行售货员问题)
在赋权图中求最小H圈是NP—难问题。理论上也已经证明：不存在多项式时间近似算法，使相对误差小于或等于某个固定的常数ε,即便是ε=1000也是如此。
(一)、边交换技术【赋权完全图中】
注：为了得到进一步的优解，可以从几个不同的初始圈开始，通过边交换技术得到几个近似最优解，然后从中选取一个近似解。
(二)、赋权完全图中最优H圈下界估计
(七)、超哈密尔顿图与超可迹图问题
(一)、超H图与超可迹图【训练逻辑演绎】
定义1 若图G是非H图，但对于G中任意点v,都有G-v是H图，则称G是超H图。
定理1 彼得森图是超H图。
定义2 若G中没有H路，但是对G中任意点v，G-v存在H路，则称G是超可迹的。
1、加莱猜想：不存在超可迹的图。 错误
2、泰特猜想：任何3连通3正则可平面图是H图。 错误
3、纳什—威廉斯猜想：每个4连通4正则图是H图。 错误
4、托特猜想：每个3连通3正则偶图是H图。 错误
5、普鲁默猜想：每个2连通图的平方是H图。 正确
定义：图G的平方\(G^2\)是这样的图:
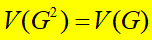
1.1 H图中H圈的计数问题。
定理：每个3正则H图至少有3个生成圈。
(二)、E图和H图的关系
1、线图概念
定义3 设G是图，G的线图L(G)定义为：
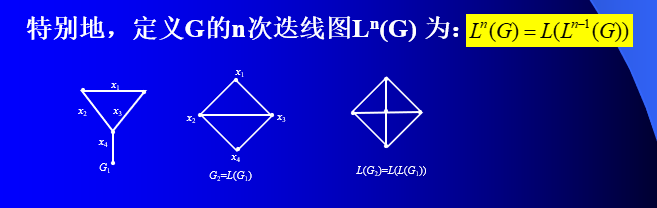
2、线图的性质
(1) 线图L(G)顶点数等于G的边数；若e=u v是G的边，则e作为L(G)的顶点度数为：d(e)=d(u)+d(v)-2 .
(2) 若G=(n, m), 则线图L(G) 边数为：
(3) 一个图同构于它的线图，当且仅当它是圈。
(4) 若图G和G1有同构的线图，则除了一个是K3而另一个是\(K_{1,3}\)外，G和G1同构。
3、从线图的角度考察E图与H图的关系
定义4 称\(S_n(G)\)是图G的n次细分图，是指将G的每条边中都插入n个2度顶点。又记：
定理3 (1)若G是E图，则L(G) 既是E图又是H图。
(2)若G是H图，则L(G)是H图。
定理4 一个图G 是E图的充要条件是\(L_3(G)\)为H图
定理5 （Chartarand）若G 是n个点的非平凡连通图，且不是一条路，则对所有\(m \geq n-3\)，\(L^m(G)\)是H图。
总结：常用符号
\(C_{m,n}\) 一种度极大非H图族
\(S_n(G)\) 是图G的n次细分图,是指将G的每条边中都插入n个2度顶点。
\(L(G)\) G的线图
总结：常用性质定理
1、欧拉图及其性质
-
连通图G是欧拉图当且仅当G的顶点度数为偶。
-
连通非欧拉图G存在欧拉迹当且仅当G中只有两个顶点度数为奇数。
2、最优欧拉环游
如果一个非负权的边赋权图G中只有两个奇度顶点u与y，求其最优欧拉环游的算法。
（1）、在u与v间求出一条最短路P；（最短路算法）
（2）、在最短路P上，给每条边添加一条平行边得G的欧拉母图G；
（3）、在G的欧拉母图G中用Fleury算法求出一条欧拉环游。
3、哈密尔顿图性质与判定
1、性质定理【必要条件】:若G为H图，则对V(G)的任一非空顶点子集S，有：\(w(G-S)\leq | S|\)
2、狄拉克定理【充分条件】:对于n≧3的单图G，如果G中有： \(\delta(G) \geq \frac{n}{2}\) ,则G是H图.
3、奥尔定理【充分条件】:对于n≧3的单图G，如果G中的任意两个不相邻顶点u与v，有：\(d(u) + d(v) \geq n\)，那么，G是H图。
4、邦迪定理（闭包定理）【充分必要条件】:图G是H图当且仅当它的闭包是H图
5、邦迪-沙瓦达定理（度序列判定法）【充分条件】:设简单图G的度序列是(d1,d2,…,dn), 这里，d1≦d2≦…≦dn,并且n≧3.若对任意的m<n/2,或有 dm>m,或有dn-m ≧ n-m,则G是H图
7、边数判定法:设G是n阶简单图。若n≥3且\(|E(G)>\left( \matrix{{n-1}\\2}\right)+1\)则G是H图；并且具有n个顶点条\(\left( \matrix{{n-1}\\2}\right)+1\)边的非H图只有\(C_{1,n}\)以及\(C_{2,5}\)
总结：一些结论
- 著名的彼德森图是非H图
- 若连通图G不是2-连通的，则G不是哈密尔顿图
- G为n阶简单图，若任意两个顶点存在d(u)+d(v)大于等于n-1，则该图G存在H路
欧拉图相关等价命题：
- 每个点的度为偶数
- 是连通图
- 边集可以划分为边不重的圈的并
欧拉图的相关结论：
- 一定是连通图
- 欧拉图不一定没有割点，比如8字形的图
- 欧拉图一定没有割边
- 非平凡的欧拉图中一定有圈
- 至少具有两个点的无环欧拉图一定是2边连通的
彼得森图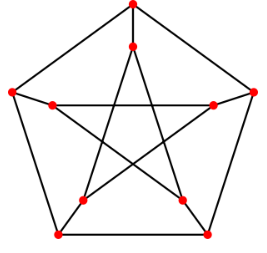
，其相关结论有：
- 点连通度为3，边连通度为3
- 是一个3正则图
- 点色数为3，边色数为4
- 半径与直径均为2
- 不是H图（删去任意顶点后为H图）
- 是不可平面图
- 存在完美匹配
- 虽然该图无割边，但也不可1-因子分解（3正则图有割边，不能1-因子分解）
- 是一个1-因子和一个2-因子的并
欧拉迹相关结论：
- 连通图存在欧拉迹当且仅当G最多有两个奇度顶点
- 有向图中存在欧拉迹，当且仅当D连通且除了两个点外，每个点出度与入度相等。而这两个点中，一个点入度比出度大1，另一个点出度比入度大1
H图相关结论：（举反例想到长度为５的圈）
- 一定没有割边
- 不一定没有割点，比如H图+自环（也是H图，而自环让该点成为了割点）
- 一个简单图是H图当且仅当它的闭包是H图
- G是n≥3的简单图，若G的闭包是完全图，则G是H图
- 若G是阶数至少为3的简单图，其中任何两个不邻接的点u和v均有d(u)+d(v)≥n，则 G是H图
- 若G是阶数至少为3的简单图，若G中每个点的度d(v)≥n/2，则G是H图
- 图G的闭包是Kn，则G是H图
- G为阶数至少为3的非H的简单图，G度弱于某个Cm,n图（度极大的H图）
- H图不一定是完全图，比如长度为5的圈
- G为阶数至少为3的H简单图，若n为奇数，则G一定不是偶图
posted on
