特征值和特征向量

一. 意义

• 从线性空间的角度看，在一个定义了内积的线性空间里，对一个N阶对称方阵进行特征分解，就是产生了该空间的N个标准正交基，然后把矩阵投影到这N个基上。N个特征向量就是N个标准正交基，而特征值的模则代表矩阵在每个基上的投影长度。 特征值越大，说明矩阵在对应的特征向量上的方差越大，功率越大，信息量越多
• 应用到最优化中，意思就是对于R的二次型，自变量在这个方向上变化的时候，对函数值的影响最大，也就是该方向上的方向导数最大。
• 应用到数据挖掘中，最大特征值对应的特征向量上包含最多的信息量。如果某几个特征值很小，说明这个方向上的信息量很小，可以用来降维，也就是删除小特征值对应方向的数据，只保留大特征值方向对应的数据，这样做以后数据量减少，但有用信息量变化不大。

二. 应用

1. 二次型优化问题：

二次型：， 其中就R是一直的二阶矩阵，R=[1, 0.5; 0.5, 1]， x是二维向量，x = [x1; x2]

1）对R进行特征分解，得到特征值：0.5， 1.5， 对应的特征向量[[-0.7071；0.7071], [0.7071；0.7071]

2) 画出y的等高线图：

 

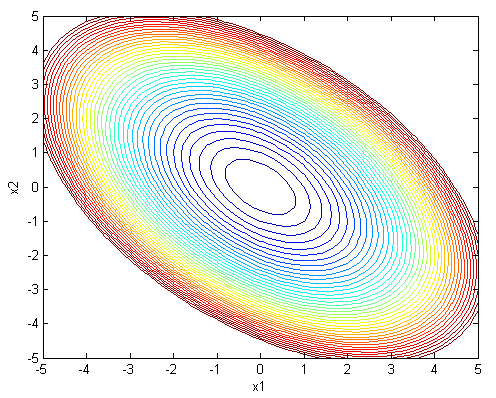
从图中可以看出，最陡峭的方向（函数值变化最快的方向）归一化以后是[0.7071；0.7071]，其对应 的特征值1.5是特征值中最大的。因为在这里这有两个特征值，所以特征值为0.5的对应的特征向量是曲面最平滑的方向。

这一点在分析算法收敛性能的时候需要用到。

 

应用2 数据降维

https://www.zhihu.com/question/21874816

三. 线性空间中数学定义

1. 特征值和特征向量的数学定义

定义1  设是一个阶方阵，是一个数，如果方程

 

           （1）

存在非零解向量，则称为的一个特征值，相应的非零解向量称为属于特征值的特征向量。

（1）式也可写成，                        

     _（2）

这是个未知数个方程的齐次线性方程组，它有非零解的充分必要条件是系数行列式

        (3)

 即   

                                                              

    上式是以为未知数的一元次方程，称为方阵的特征方程． 其左端是的次多项式，记作，称为方阵的特征多项式。

                                                  =₌ 

　　　　　　　　　　　　　　　　　　　　　　=

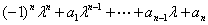
显然，的特征值就是特征方程的解．特征方程在复数范围内恒有解，其个数为方程的次数（重根按重数计算），因此，阶矩阵有个特征值．

设阶矩阵的特征值为由多项式的根与系数之间的关系，不难证明

（ⅰ）

（ⅱ））

_若为 的一个特征值，则一定是方程的根, 因此又称特征根，若为方程的重根，则称为的重特征根．方程 的每一个非零解向量都是相应于的特征向量，于是我们可以得到求矩阵的全部特征值和特征向量的方法如下：

     第一步：计算的特征多项式；

     第二步：求出特征方程的全部根，即为的全部特征值

     第三步：对于的每一个特征值，求出齐次线性方程组：

            

的一个基础解系，则的属于特征值的全部特征向量是（其中是不全为零的任意实数）．

例如：

求矩阵

  的特征值和特征向量

 

解：的特征多项式：

 =₌=

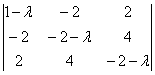所以的特征值为==2（二重根），.

对于==2，解齐次线性方程组．由

    ，

 得基础解系为：    

因此，属于==2的全部特征向量为：不同时为零.

对于，解齐次线性方程组．由

 

   ，

得基础解系为：

 

因此，属于的全部特征向量为：

 

2. 特征向量之间的关系

定理1 　属于不同特征值的特征向量一定线性无关.

证明 　设是矩阵的不同特征值，而分别是属于的特征向量，要证是线性无关的.我们对特征值的个数作数学归纳法证明.

当时,由于特征向量不为零,所以结论显然成立.

当＞1时,假设时结论成立.

由于是的不同特征值,而是属于的特征向量,因此

   

如果存在一组实数使

 则上式两边乘以得

另一方面,     ,即

两式相减：

 

由归纳假设,  线性无关,因此

   

 

而互不相同,所以．于是(3)式变为

因,于是．可见线性无关．

 

3. 相似矩阵

定义2  设、都是阶方阵，若存在满秩矩阵， 使得

 

则称与相似，记作 ，且满秩矩阵称为将变为的相似变换矩阵．

 

“相似”是矩阵间的一种关系，这种关系具有如下性质：

⑴ 反身性：～ ；

⑵ 对称性：若 ～ ，则～ ；

 

⑶ 传递性：若～， ～ ，则～． 

相似矩阵还具有下列性质：

 

定理2  相似矩阵有相同的特征多项式，因而有相同的特征值.

证明　　设～， 则存在满秩矩阵，使

于是：

 

推论  若阶矩阵与对角矩阵

 

相似，则即是的个特征值．

定理3 设是矩阵的属于特征值的特征向量,且~,即存在满秩矩阵使,则是矩阵的属于的特征向量．

 

定理4 阶矩阵与对角矩阵相似的充分必要条件是：矩阵有个线性无关的分别属于特征值的特征向量（中可以有相同的值）．

 

例2　 设矩阵，求一个满秩矩阵，使为对角矩阵．

1. 求特征值

  

所以的特征值为.

2. 根据特征值求特征项向量：

对于 解齐次线性方程组，得基础解系，即为的两个特征向量

对于=2，解齐次线性方程组，得基础解系，即为的一个特征向量.

 

 

3. 判断是否能相似于对角矩阵

显然是线性无关的，且个数为3，所以能相似于对角矩阵，取：

 

 即有：

 4. 向量组的正交性

在解析几何中，二维、三维向量的长度以及夹角等度量性质都可以用向量的内积来表示，现在我们把内积推广到维向量中．

定义3  设有维向量，，令

 

  =，则称为向量和的内积．

 

定义4  令

||=

 

称||为维向量的模（或长度）．

 

定义5  当|| ≠0，||≠0时，

 　

称为维向量、的夹角．

特别地：当=0时，，因此有当=0时，称向量与正交．（显然，若=0，则与任何向量都正交）．

定义6   已知个非零向量，若=0 ，则称为正交向量组．

 

定义7 若向量组为正交向量组，且||=1，则称　为标准正交向量组．

例如，维单位向量组=，，是正交向量组．

正交向量组有下述重要性质：

定理5  正交向量组是线性无关的向量组

定理6　设向量组线性无关，由此可作出含有个向量的正交向量组_，其中：

 ， ，…… 

再取：

   

 

则为标准正交向量组．

上述从线性无关向量组导出正交向量组的过程称为施密特（Schimidt）正交化过程．它不仅满足与等价，还满足：对任何，向量组与等价

 

 

例4 设 求一个正交矩阵，使为对角矩阵.

解：1. 求特征值：

  

 

所以的特征值，.

2. 求特征向量及标准正交矩阵：

对于，解齐次线性方程组，得基础解系：

 

因此属于的标准特征向量为：

对于，解齐次线性方程组，得基础解系：

         

这两个向量恰好正交，将其单位化即得两个属于的标准正交向量：

 

 

 ，     

 

于是得正交矩阵：

 

 

易验证：

.

 

详情见：http://course.tjau.edu.cn/xianxingdaishu/jiao/5.htm

 

三. 应用