图
1.学习总结
1.1思维导图
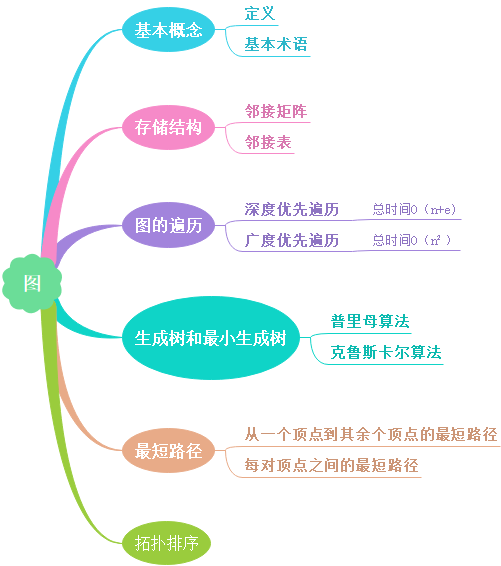
1.2图结构学习体会
- 深度遍历算法
- 从图中某个初始顶点v出发,首先访问初始顶点v,然后选择一个与顶点v相邻且没被访问过的顶点w为初始顶点,再从w出发进行深度优先遍历,直到图中与当前顶点v邻接的所有顶点都被访问过为止。
- 广度遍历算法
- 首先访问初始顶点v,接着访问顶点v的所有未被访问的邻接点,然后按照次序,访问每一个顶点的所有未被访问的邻接点,以此类推,直到图中所有和初始顶点v有路径相通的顶点都被访问过为止。
- Prim和Kruscal算法
- 普里姆算法:
1).输入:一个加权连通图,其中顶点集合为V,边集合为E;2).初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;3).重复下列操作,直到Vnew = V:a.在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);b.将v加入集合Vnew中,将<u, v>边加入集合Enew中;4).输出:使用集合Vnew和Enew来描述所得到的最小生成树。
- 克鲁斯卡尔算法:
-
克鲁斯卡尔算法是一种用来寻找最小生成树的算法。在剩下的所有未选取的边中,找最小边,如果和已选取的边构成回路,则放弃,选取次小边。
- Dijkstra算法
- 是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
- 拓扑排序算法
- 对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列
2.PTA实验作业
1.图着色问题
1.1设计思路:
当t=1时,对当前第t个顶点开始着色:若t>n,则已求得一个解,输出着色方案即可。否则,依次对顶点t着色1-m, 若t与所有其它相邻顶点无颜色冲突,则继续为下一顶点着色;否则,回溯,测试下一颜色
1.2 代码截图


1.3 提交列表
2.排座位
2.1设计思路:
此题用并查集算法较为简单。
2.2代码截图

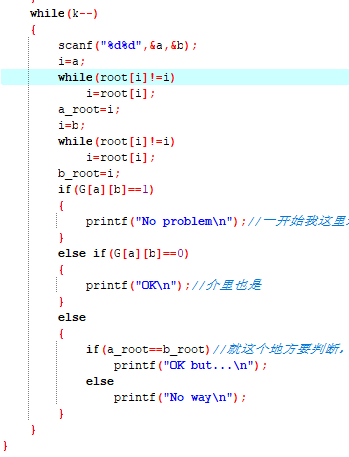
2.3提交列表
3.公路村村通
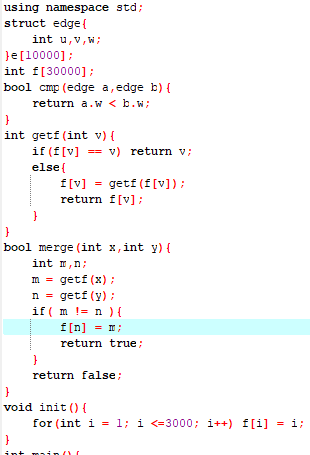
代码截图

3.本周最后排名

总分:80
4.阅读代码:
#include <stdio.h>
#include <stdlib.h>
struct Node {
int value;
int indegree;
struct Node *next;
};
//初始化邻接表
struct Node* initAdjList(int n) {
struct Node* headers;
headers = (struct Node*)malloc(sizeof(struct Node) * n);
int i = 0;
for(i; i < n; i++) {
headers[i].next = NULL;
headers[i].value = 0;
headers[i].indegree = 0;
}
return headers;
}
void addAdj(struct Node* header, int m, int n) {
struct Node* p = &header[m];
p->value++;
while(p->next != NULL)
p = p->next;
p->next = (struct Node*)malloc(sizeof(struct Node));
p->next->value = n;
p->next->next = NULL;
}
//打印邻接表
void printAdjList(struct Node* header, int n) {
int i = 0;
for(i; i < n; i++) {
struct Node* p = &header[i];
printf("Number of %d' adj : %d\t", i, p->value);
while(p->next!= NULL) {
printf("%d --->%d\t", i, p->next->value);
p = p->next;
}
printf("\n");
}
}
//拓扑排序
int* topSort(struct Node* headers, int n) {
int* zeroStack = (int*)malloc(sizeof(int) * n);
int* result = (int*)malloc(sizeof(int) * n);
int count = 0;
int pIndex = -1;
int i = 0;
while(i < n) {
struct Node* p = &headers[i];
//入度为0,直接进栈
if(p->indegree == 0)
zeroStack[++pIndex] = i;
i++;
}
while(1) {
//从top里面出栈一个Node Index
int zeroIndex = zeroStack[pIndex--];
result[count++] = zeroIndex;
struct Node* zeroNode = &headers[zeroIndex];
//将zeroNode的连接点,对应的头结点的值减一
while(zeroNode->next != NULL) {
struct Node* q = &headers[zeroNode->next->value];
if(--q->indegree == 0)
zeroStack[++pIndex] = zeroNode->next->value;
zeroNode = zeroNode->next;
}
//栈空
if(pIndex < 0)
break;
}
return result;
}
int main()
{
int a[7][7] = { {0,1,1,1,0,0,0},
{0,0,0,0,1,1,0},
{0,0,0,0,0,0,1},
{0,0,1,0,0,1,1},
{0,0,0,1,0,0,1},
{0,0,0,0,0,0,0},
{0,0,0,0,0,1,0}
};
int n = 7;
struct Node* headers = initAdjList(n);
int i = 0;
int j = 0;
for(i = 0; i < n; i++)
for(j = 0; j < n; j++) {
if(a[i][j] == 1)
addAdj(headers, i, j);
}
//生成各节点indegree
for(i = 0; i < n; i++) {
struct Node* p = &headers[i];
while(p->next != NULL) {
headers[p->next->value].indegree++;
p = p->next;
}
}
int* q = topSort(headers, n);
printAdjList(headers, n);
for(i = 0; i < n; i++) {
printf("%d \n", *q++ + 1);
}
return 0;
}







 浙公网安备 33010602011771号
浙公网安备 33010602011771号