Legendre polynomials
In mathematics, Legendre functions are solutions to Legendre's differential equation:
![{d \over dx} \left[ (1-x^2) {d \over dx} P_n(x) \right] + n(n+1)P_n(x) = 0.](https://upload.wikimedia.org/math/5/2/b/52bff80109b66b45a6fb0ea62522a03f.png)
In particular, it occurs when solving Laplace's equation (and relatedpartial differential equations) in spherical coordinates.

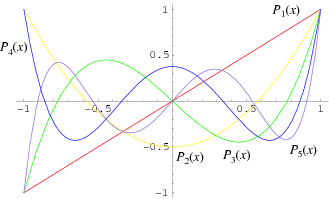
The polynomials may be denoted by Pn(x) , called the Legendre polynomial of order n. The polynomials are either even or odd functions of x for even or odd orders n. The first few polynomials are shown below.
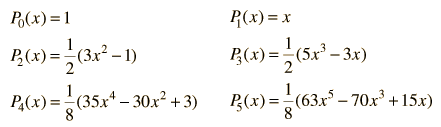
The general form of a Legendre polynomial of order n is given by the sum:
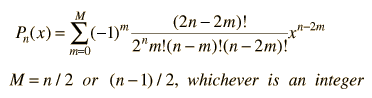
From the Legendre polynomials can be generated another important class of functions for physical problems, the associated Legendre functions.
OPTIMISM, PASSION & HARDWORK



 浙公网安备 33010602011771号
浙公网安备 33010602011771号