P2 价值学习

Deep Q-Network（DQN)

\[对于一个游戏来说，我们的目标是为了赢得游戏（也就相当于是要去找到一个最大的总和奖励\\那么现在的目标有了，问题就是如果我们知道一个Q^*函数，应该如何做决策，也就是如何找到\\最优的动作\\ 但实际上，我们在开始是不知道Q^*的 因此我们的解决方法是 DQN网络\\ 我们对于Q(s,a;w)来说，w是神经网络的输入 s表示输出的数值 a是选择的动作\\ 我们通过不断的训练来让这个Q函数不断地接近Q^*函数 也就是我们最后得到的最优解 \]

例如：

对于超级玛丽的游戏，我们可以对于当前的情况画面来作为输入，通过一个卷积层来将输入转化为特征向量，然后再通过一个连接层将图片映射成突出的向量（即对于每个动作的打分，即对于上面的Q（s,a;w）

如何训练DQN ？ 常用的算法就是

Temporal Difference（TD）learning——时序差分学习

例子：

\[实际问题:从纽约出发去亚特兰大 \\ 初始：模型Q(w)提示全程需要1000分钟\\ 问：怎样更新模型Q来得到更加精确的时间\\ 过程：1.开始模型Q（w）给出当前预测值 q=1000\\ 2.实际过程旅行完花费860分钟 target y=860 \\ 3.我们假定损失函数：L=1/2（q-y）^2 \\ 4.我们用L对w求导 如上图所示 \\ 5.梯度出来之后 我们可以用梯度下降来更新下一次的w_{t+1} \ \ 其中α是学习率或者步长 \\ 通过梯度下降得到的预测值w_{t+1}更加接近实际情况 因为他通过梯度下降减少了损失函数\\ 缺点：这种算法比较难应付\ 因为每一次都需要完成全部的旅行才能对模型更新一次\ \]

进阶：能否不需要完成全部旅行，即完成部分旅行就可以进行一次模型的更新

\[现在 假设从纽约城出发去亚特兰大，中途到达华盛顿的时候花费了300分钟\\然后这个时候出了故障需要短暂调整，此时模型告诉我们\ 从华盛顿到亚特兰大需要600分钟\\ 此时，我们之前花费的300+预测的600=900分钟 这比模型刚开始预测的1000分钟\\来说,要更加的精准一点\ 此时这个900\ 我们就称为TD\ target\\ 此时的损失函数和梯度下降结算下一次的W_{t+1}如上所示 \]

TD算法的目标就是为了让TD error接近0 0也就意味着实际时间和预测时间相等，所以TD算法要用梯度下降来减少TD error

现在将例子转化到深度强化学习思想中：

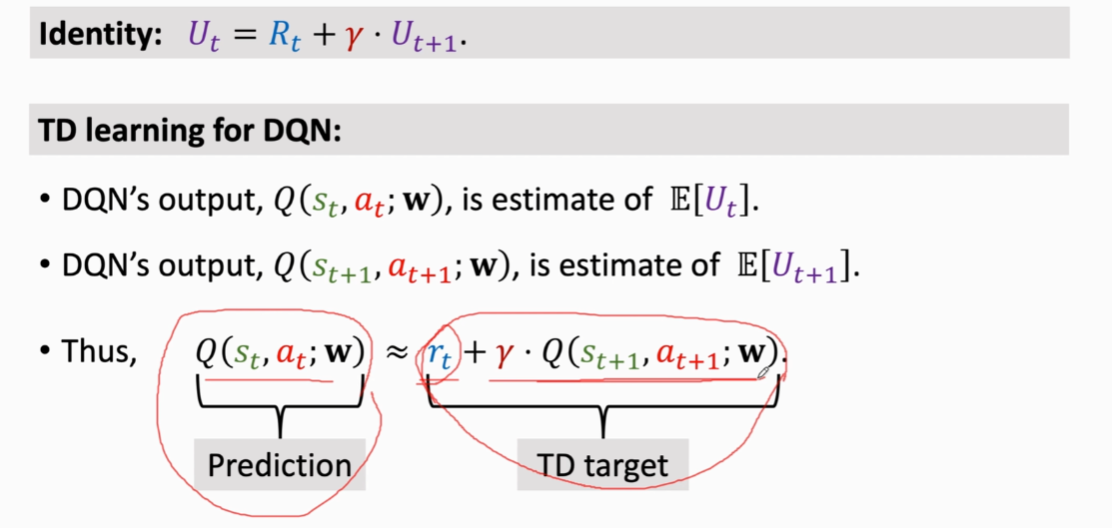
\[在上述这个驾驶时间的例子中，我们可以提炼出一个等式\\ T_{NYC→ATL}≈T_{NYC→DC}+T_{DC→ATL}\\ 这个式子包含三部分，第一部分是模块第一次预测的时间，第二部分是真实时间，\\第三部分则是第二次预测的接下来路程的时间\\ 由此类比到深度强化学习中就得到了后面这个等式（或者说一个重要等式）\\ Q(S_t,a_t;w)≈r_t+γ*Q(s_{t+1},a_{t+1};w)\\ 核心就是等式包含两个预测值和一个真实值 \]

证明，之前的折扣回报，推导如下：

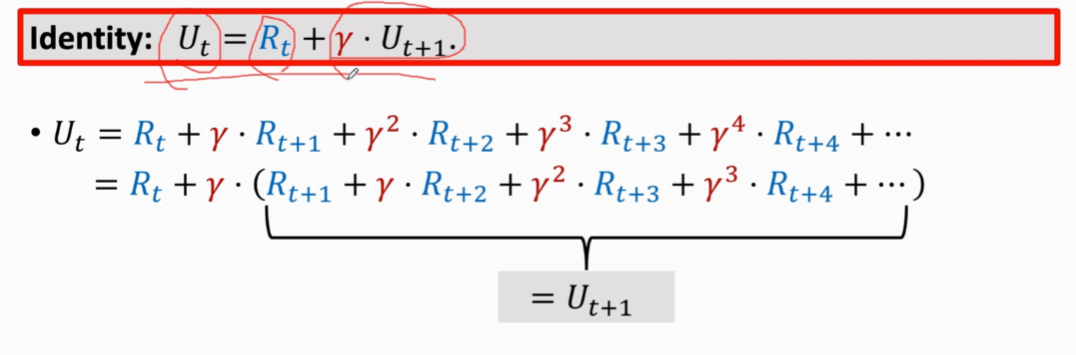
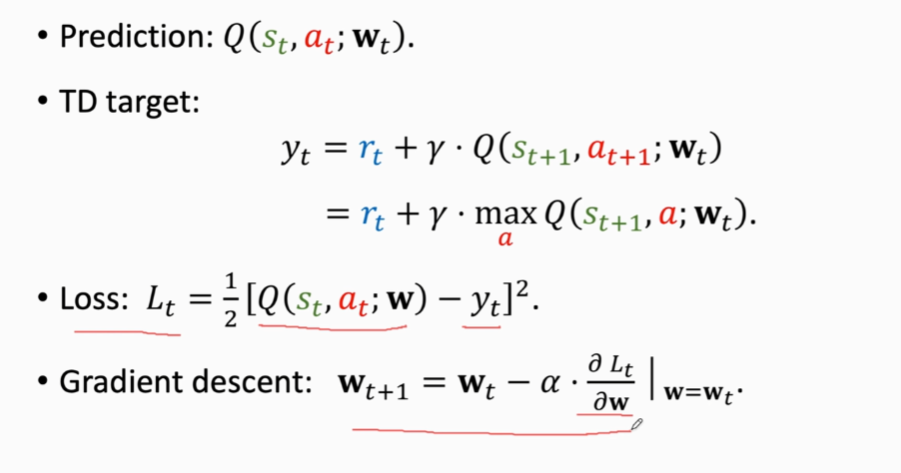
总结 TD算法的过程如下：