lenyan的算法笔记(日常更新)
笔记
2024年开始啦
《lenyan算法笔记》
网址会优先更新。- - -
可能有点菜,误喷。😊🤣
📚 《lenyan算法笔记》——探索算法的乐趣
🌟 欢迎来到《lenyan算法笔记》!这是我日常记录和分享算法学习心得的地方,无论你是初学者还是已经有一定经验的程序员,都能在这里找到有趣的内容。
🧠 记录学习心得:我用通俗易懂的语言记录了自己学习算法的过程和体会,希望能够帮助到更多有相同兴趣的朋友。
💻 分享实用代码:每篇笔记都附带了一些实用的代码示例,这些示例不仅是我学习的成果,也可以作为你学习的参考。
📈 持续学习进步:算法学习是一条持续的道路,我会不断地更新笔记内容,记录自己的学习进步,与你一起成长。
🔍 分享交流:如果你对我的笔记有任何疑问或建议,都欢迎在评论区与我交流,让我们一起探讨算法的乐趣!
🚀 如果你也对算法感兴趣,不妨点击链接,一起来探索《lenyan算法笔记》吧:《lenyan算法笔记》 🔥
d47e8eac-b5d5-4685-bc4f-7af13a2997ef
4/1
计算几何
Π的定义
#define Pi 3.14159265358979323846
double pi = acos(-1.0)
三角行坐标面积求

#include <bits/stdc++.h>
using namespace std;
int main()
{
// 请在此输入您的代码
int n;
cin>>n;
for(int i=0;i<n;i++){
double x1,x2,x3,y1,y2,y3;//注意题目说是实数,即包含小数,用double
cin>>x1>>y1>>x2>>y2>>x3>>y3;
double a1=x2-x1,b1=y2-y1,a2=x3-x1,b2=y3-y1;
double result=fabs(a1*b2-a2*b1)*1.0/2;
printf("%.2f\n",result);
}
return 0;
}
//三角形面积坐标式
// S=1/2*|(a1b2-a2b1)|;
// a1=x2-x1,b1=y2-y1,a2=x3-x1,b2=y3-y1
C++保留小数
#include <iomanip>
...
cout<<fixed<<setprecision(n)<<shu; //shu就是你要保留小数的数字;
...
C++ 保留N位小数的几种方法_c++保留小数-CSDN博客
浮点误差
3/31
常用算法定义的
using ll = long long;
using ld = long double;
using unl = __int128;
using ull = unsigned long long;
using Pair = pair<int,int>;
#define x first
#define y second
#define inf 1`000`000`000`000`000ll
3/28
接上一天的DFS模板
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int n, m, x, y, ax, ay, k;
int nxy[4][2] = { 0,1,1,0,0,-1,-1,0 }; // 方向数组,用于表示四个方向上的移动
int vis[N][N]; // 访问数组
int h[N][N]; // 存储高度信息
int dp[N][N][2]; // 动态规划数组,dp[i][j][flag] 表示从起点到达点 (i, j),且是否使用了加能量的标记 flag
bool dfs(int x, int y, int flag)
{
if (x == ax && y == ay) return true; // 如果当前位置是目标位置,则返回 true
if (dp[x][y][flag] != -1) return dp[x][y][flag]; // 如果当前状态已经计算过了,则直接返回对应的结果
for (int i = 0; i < 4; i++)
{
int nx = x + nxy[i][0]; // 计算下一个位置的横坐标
int ny = y + nxy[i][1]; // 计算下一个位置的纵坐标
if (nx<1 || ny<1 || nx>n || ny>m)continue; // 如果下一个位置超出边界,则跳过当前循环
if (!flag)
{
if (h[x][y] > h[nx][ny] && dfs(nx, ny, 0)) // 如果当前位置高度大于下一个位置且不使用加能量,则尝试继续向下一个位置移动
return dp[x][y][flag] = true; // 如果成功到达目标位置,则返回 true
if (h[x][y] + k > h[nx][ny] && dfs(nx, ny, 1)) // 如果当前位置高度加能量后大于下一个位置且使用加能量,则尝试继续向下一个位置移动
return dp[x][y][flag] = true; // 如果成功到达目标位置,则返回 true
}
else {
if (h[x][y] > h[nx][ny] && dfs(nx, ny, 1)) // 如果当前位置高度大于下一个位置且使用加能量,则尝试继续向下一个位置移动
return dp[x][y][flag] = true; // 如果成功到达目标位置,则返回 true
}
}
return dp[x][y][flag] = false; // 如果无法到达目标位置,则返回 false
}
int main()
{
memset(dp, -1, sizeof dp); // 初始化动态规划数组为 -1
cin >> n >> m >> k; // 输入 n、m 和 k 的值
cin >> x >> y >> ax >> ay; // 输入起点和终点的坐标
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
cin >> h[i][j]; // 输入高度信息
}
cout << (dfs(x, y, 0) ? "Yes" : "No") << '\n'; // 输出能否到达终点的结果
return 0;
}
goto用法:
#include <stdio.h>
int main() {
int i, t, sum = 0;
// 外层循环,从 i=1 开始递增
for (i = 1;; i++) {
// 内层循环,对当前的 i 进行逐位判断
for (t = i; t != 0; t /= 10)
if (t % 10 == 1) // 如果当前位为1,则sum加1
sum++;
// 如果sum大于等于2021,则跳出外层循环
if (sum >= 2021)
goto end;
}
end:
// 输出最终符合条件的 i 的值
printf("%d", i);
return 0;
}
在C++中,goto语句用于无条件地将控制转移到程序中的标记语句。下面是goto语句的一般用法:
cppCopy code
#include <iostream>
using namespace std;
int main() {
int num = 10;
// 标记语句
start:
cout << "num = " << num << endl;
num--;
// 检查条件
if (num > 0) {
goto start; // 转移到标记语句
}
return 0;
}
在这个例子中,标记语句start:被定义在循环之前。在循环中,程序输出num的值,然后递减num。当num大于0时,程序通过goto语句跳转到标记语句start:处,从而形成了一个简单的循环。
虽然goto语句在某些情况下可以简化代码,但它通常被认为是一种不良的编程实践,因为它可以导致代码变得难以理解和维护。使用结构化编程,如循环和条件语句,通常会更清晰地表达程序逻辑。
3/27
KMP算法
#include <bits/stdc++.h>
const int N=1e6+9;
using namespace std;
char a[N],b[N];
int nex[N]; // next 数组,用于记录字符串 b 的最长公共前后缀长度
int main()
{
cin>>a+1>>b+1; // 从输入中读取两个字符串 a 和 b
int n=strlen(a+1); // 计算字符串 a 的长度
int m=strlen(b+1); // 计算字符串 b 的长度
// 计算 next 数组
for(int i=2,j=0;i<=m;i++){
while(j&&b[i]!=b[j+1]) j=nex[j];
if(b[i]==b[j+1]) j++;
nex[i]=j;
}
int ans=0; // 最大匹配长度
int cnt=0; // 当前匹配的连续长度
// 在字符串 a 中匹配字符串 b
for(int i=1,j=0;i-m+1<=n;i++){
while(j&&a[i]!=b[j+1]) j=nex[j],cnt=0; // 不匹配时根据 next 数组更新 j,重置 cnt
if(a[i]==b[j+1]) j++,cnt++; // 匹配成功时更新 j 和 cnt
ans=max(ans,cnt); // 更新最大匹配长度
if(j==m) break; // 如果完全匹配则跳出循环
}
cout<<ans; // 输出最大匹配长度
return 0;
}
DFS经典题目
混境之地2
染色法或者DFS记忆化搜索

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010;
char g[N][N]; // 地图数组
int a, b, c, d; // 起点和终点坐标
int n, m; // 地图的行数和列数
int dp[N][N][2]; // 动态规划数组,用于记忆化搜索
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, -1, 0, 1}; // 方向数组,表示上下左右移动
bool st[N][N]; // 记录是否访问过某个点
// 深度优先搜索函数,参数分别表示当前位置的横纵坐标以及标志位
bool dfs(int x, int y, int flag) {
if (x == c && y == d) { // 如果当前位置是终点,则返回true
return true;
}
if (dp[x][y][flag] != -1) // 如果当前状态已经搜索过,则直接返回之前的结果
return dp[x][y][flag];
for (int i = 0; i < 4; i++) { // 枚举四个方向
int tx = x + dx[i], ty = y + dy[i]; // 计算下一个位置的坐标
if (tx < 1 || tx > n || ty < 1 || ty > m) // 如果下一个位置超出地图范围,则跳过
continue;
if (st[tx][ty]) // 如果下一个位置已经被访问过,则跳过
continue;
st[tx][ty] = true; // 标记下一个位置为已访问
if (flag) { // 如果当前标志位为1
if (g[tx][ty] == '.' && dfs(tx, ty, 1)) // 如果下一个位置是空地且可以到达终点,则返回true
return dp[x][y][flag] = true;
if (g[tx][ty] == '#' && dfs(tx, ty, 0)) // 如果下一个位置是障碍物且可以到达终点,则返回true
return dp[x][y][flag] = true;
} else { // 如果当前标志位为0
if (g[tx][ty] == '.' && dfs(tx, ty, 0)) // 如果下一个位置是空地且可以到达终点,则返回true
return dp[x][y][flag] = true;
}
st[tx][ty] = false; // 回溯,标记下一个位置为未访问
}
return dp[x][y][flag] = false; // 如果无法到达终点,则返回false
}
int main() {
cin >> n >> m; // 输入地图的行数和列数
cin >> a >> b >> c >> d; // 输入起点和终点的坐标
for (int i = 1; i <= n; i++) { // 输入地图
for (int j = 1; j <= m; j++) {
cin >> g[i][j];
}
}
memset(dp, -1, sizeof dp); // 初始化动态规划数组为-1
if (dfs(a, b, 1)) // 如果从起点能够到达终点,则输出"Yes"
puts("Yes");
else // 否则输出"No"
puts("No");
return 0;
}
记忆化搜索模板
#include <iostream>
#include <vector>
#include <cstring> // 用于memset函数
using namespace std;
const int MAX_N = 100; // 定义最大的状态空间大小
// 记忆化搜索数组
int memo[MAX_N][MAX_N]; // 假设每个状态需要两个参数
// 记忆化搜索函数,参数通常为当前状态的参数
int dp(int param1, int param2) {
// 如果当前状态已经计算过,则直接返回结果
if (memo[param1][param2] != -1)
return memo[param1][param2];
// 如果当前状态未计算过,则进行计算,并将结果保存在memo数组中
// 这里可以根据具体问题的要求进行状态转移和计算
// 示例:当前状态的计算过程
int result = 0; // 假设计算的结果为整数
// 这里可以根据实际问题进行状态转移和计算
// result = ...
// 更新memo数组
memo[param1][param2] = result;
// 返回计算结果
return result;
}
int main() {
// 初始化memo数组,通常初始化为一个特殊的值,例如-1
memset(memo, -1, sizeof(memo));
// 示例调用记忆化搜索函数
int ans = dp(0, 0); // 假设需要计算从状态(0, 0)开始的结果
// 输出结果
cout << "Result: " << ans << endl;
return 0;
}
3/26
DFS基础题
黄金树
#include<bits/stdc++.h>
using namespace std;
struct tree {
int l; // 左子节点索引
int r; // 右子节点索引
};
const int N = 1e5 + 5;
tree a[N]; // 存储树的节点信息
int w[N], n; // w数组存储每个节点的权重,n表示树的节点数
vector<int> sum; // 存储路径的权重和
// 深度优先搜索函数
// dep: 当前节点索引
// key: 当前节点所在路径的黄金指数(路径深度)
void dfs(int dep, int key) {
// 如果当前节点的黄金指数为0,则将当前节点的权重存储到sum中
if (key == 0)
sum.push_back(w[dep]);
// 如果当前节点存在左子节点,则递归调用dfs函数,将黄金指数增加1
if (a[dep].l != -1)
dfs(a[dep].l, key + 1);
// 如果当前节点存在右子节点,则递归调用dfs函数,将黄金指数减少1
if (a[dep].r != -1)
dfs(a[dep].r, key - 1);
}
int main() {
// 从标准输入读取树的节点数
cin >> n;
// 循环读取每个节点的权重,并存储到数组w中
for (int i = 1; i <= n; i++)
cin >> w[i];
// 循环读取每个节点的左右子节点的索引,并存储到数组a中
for (int i = 1; i <= n; i++)
cin >> a[i].l >> a[i].r;
// 调用dfs函数,从根节点开始遍历树
dfs(1, 0);
int ans = 0;
// 计算sum中所有元素的和,即为路径的权重和
for (auto i : sum) {
ans += i;
}
// 输出结果
cout << ans;
return 0;
}
3/25
isalpha isalnum isdigit islower isupper
【C++常用函数】isalpha、isalnum、isdigit、islower、isupper用法_std::isalpha详解-CSDN博客
- isalpha()用来判断一个字符是否为字母
- isalnum用来判断一个字符是否为数字或者字母,也就是说判断一个字符是否属于a~ z||A~ Z||0~9。
- isdigit() 用来检测一个字符是否是十进制数字0-9
- islower()用来判断一个字符是否为小写字母,也就是是否属于a~z。
- isupper()和islower相反,用来判断一个字符是否为大写字母。
- 以上如果满足相应条件则返回非零,否则返回零。
#include <iostream>//输入输出
#include <ctype.h>//isalpha、isalnum、isdigit、islower、isupper
using namespace std;
void main() {
cout << isalnum('a') << ' '<< isalnum('9') << endl;
cout << isalpha('a') << ' '<< isalpha('9') <<endl;
cout << isdigit('a') << ' '<< isdigit('9') <<' '<< endl;
cout << islower('a') << ' '<< islower('X') <<' '<< islower('9') << endl;
cout << isupper('a') << ' '<< isupper('Z') <<' '<< isupper('9') << endl;
}
输出结果:

gets / getline
C++字符串读入函数(gets&getline)_getline和gets的区别-CSDN博客
总结如下:
- gets 函数位于 头文件中,用于从标准输入流中读取字符串直至换行符或文件结束符(EOF)出现,然后将读取的结果存储在指定的字符数组中。
- 返回值:成功读取返回与参数 buffer 相同的指针,遇到错误或EOF返回 NULL。
- 参数:char 类型数组的首地址。
- 注意:由于 gets 存在安全性问题,可能导致缓冲区溢出,因此应尽量避免使用。
- getline 函数位于 头文件中,用于从输入流中读取字符串,存储在 string 类型的对象中。
- 可以指定结束符,如果不指定则默认为换行符或EOF。
- 返回值:成功读取时返回读取的字节数,失败返回 -1。
- 参数:读入方式(通常为 cin)、string 类型的字符串、可选的结束字符。
- 与 gets 的不同之处在于可以读取到 string 类型的对象,并且可以指定结束字符。
总的来说,gets 主要用于读取字符数组,而 getline 主要用于读取字符串对象,并且可以指定结束字符。在实际应用中,尽量使用 getline 来避免安全性问题。
3/24
字符串快速幂
1.因为幂本质是乘法,所以在任何地方都可以取模
2.其次是P太大了,字符串读入,下面是两种遍历P求字符串快速幂的方法(第二种是秦九韶求多项式法)
3.不需要快速幂,因为每一次最多求10次幂,t个样例将每个P遍历一次,总的时间复杂度为 O(10*P的总长度)约等于 2e6,实测2ms就过了
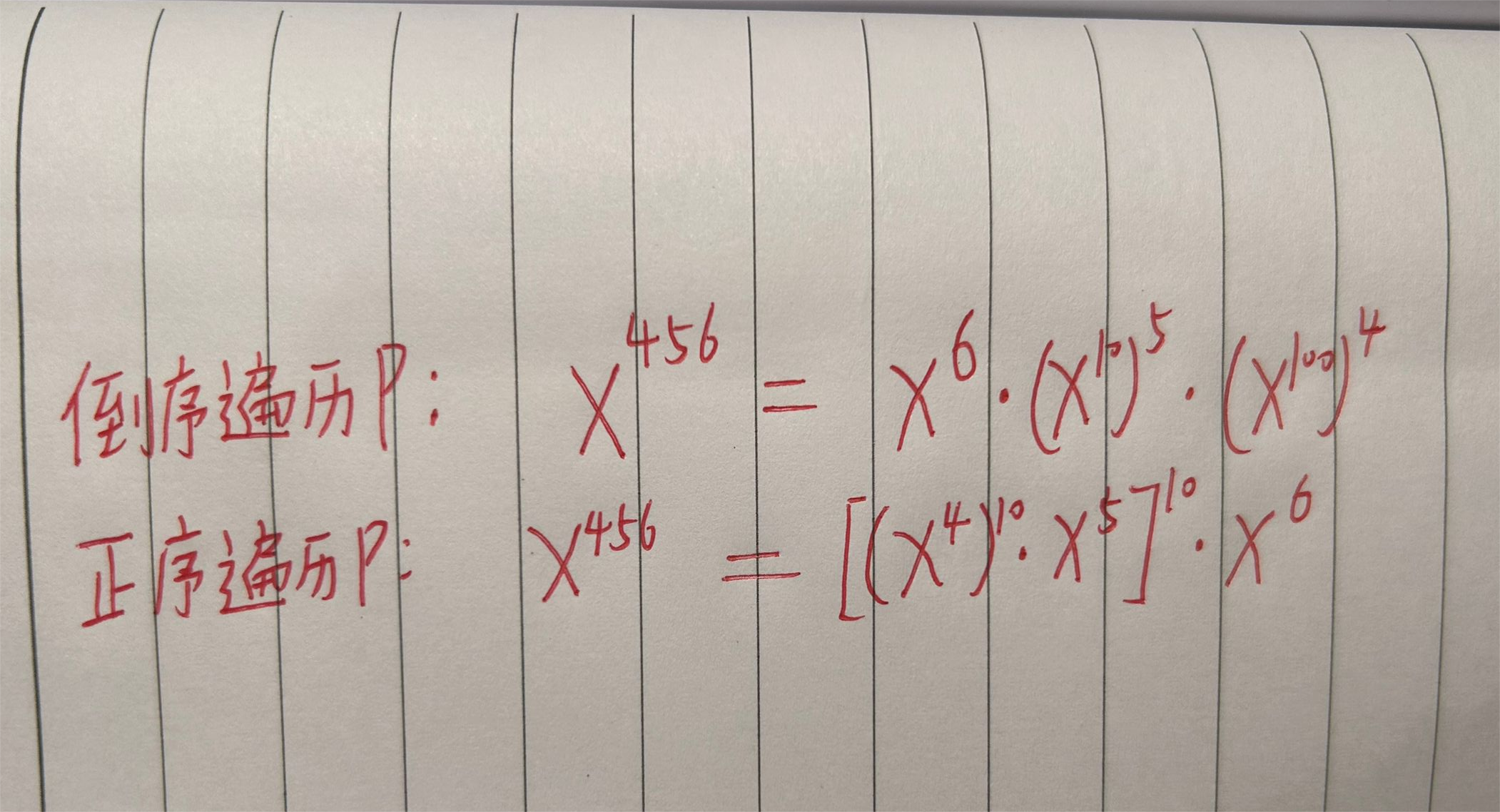
#include<bits/stdc++.h>
using namespace std;
int _pow(int a,int n,int p)//求a^n普通幂,对p取模
{
int res=1;
while(n--)res=res*a%p;
return res;
}
int main()
{
int t;
cin>>t;
while(t--)
{
int x;
string p;
cin>>x>>p;
int ans=1;
for(int i=p.size()-1;i>=0;i--)//倒序遍历
{
ans=(ans*_pow(x,p[i]-'0',10))%10;
x=_pow(x,10,10)%10;//每一次 x=x^10
}
cout<<ans<<endl;
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
int _pow(int a,int n,int p)//求a^n普通幂,对p取模
{
int res=1;
while(n--)res=res*a%p;
return res;
}
int main()
{
int t;
cin>>t;
int x;
string p;
while(t--)
{
cin>>x>>p;
int ans=1;
for(int i=0;i<p.size();i++)//正序枚举
ans=(_pow(ans,10,10)*_pow(x,p[i]-'0',10) )%10;//每一次计算前ans变成ans^10
cout<<ans<<endl;
}
return 0;
}
DFS基本模板注意
#include <iostream>
using namespace std;
using ll = long long;
int mp[105][105]; // 定义二维数组mp来存储输入的矩阵元素
int vis[105][105]; // 定义二维数组vis来标记矩阵中的元素是否被访问过
int nxy[4][2] = {1, 0, -1, 0, 0, 1, 0, -1}; // 方向数组,表示四个方向上的移动
int N, M; // 矩阵的行数和列数
ll ans, tmp; // 最终结果和临时结果
void dfs(int x, int y) {
if (x < 1 || y < 1 || x > N || y > M || mp[x][y] == 0 || vis[x][y]) return; // 如果越界或者当前位置为0或者已经访问过,则返回
vis[x][y] = 1; // 标记当前位置为已访问
tmp += mp[x][y]; // 累加当前位置的值到临时结果中
for (int i = 0; i < 4; i++) { // 对当前位置的四个相邻位置进行深度优先搜索
int nx = x + nxy[i][0]; // 计算下一个位置的行坐标
int ny = y + nxy[i][1]; // 计算下一个位置的列坐标
dfs(nx, ny); // 递归搜索下一个位置
}
}
int main() {
cin >> N >> M; // 读入矩阵的行数和列数
for (int i = 1; i <= N; i++)
for (int j = 1; j <= M; j++)
cin >> mp[i][j]; // 依次读入矩阵的元素
for (int i = 1; i <= N; i++)
for (int j = 1; j <= M; j++) {
if (mp[i][j] == 0 || vis[i][j]) continue; // 如果当前位置的值为0或者已经访问过,则跳过
tmp = 0; // 初始化临时结果为0
dfs(i, j); // 以当前位置作为起点进行深度优先搜索
ans = max(tmp, ans); // 更新最大和ans的值
}
cout << ans << endl; // 输出最大和ans的结果
return 0;
}

3/23
重载结构体中的大于小于符号
重载结构体中的大于小于符号,为了方便sort或者优先队列priority_queue的使用。
其实只用重载其中的小于符号即可。
正常次序的重载:
struct node{
int w;
bool operator <(const node a)const{//记住!!!
return w<a.w;
}
}e[maxn];
priority_queue<node> q; //此时的优先队列是按结构体的w值,从大到小排列
sort(e,e+n);//按照结构体的w值,从小到大进行排序
相反次序的重载:
struct node{
int w;
bool operator <(const node a)const{
return a.w<w;//在这里改变一下位置可
}
}e[maxn];
priority_queue<node> q; //此时的优先队列是按结构体的w值,从小到大排列
sort(e,e+n);//按照结构体的w值,从大到小进行排序
bool operator < (const node &a)const { // 距离从小到大排序
return len > a.len;
}
3/22
快速求区间质数
【题解】2023年第六届传智杯复赛第二场题解_ACM竞赛_ACM/CSP/ICPC/CCPC/比赛经验/题解/资讯_牛客竞赛OJ_牛客网
#include<bits/stdc++.h> // 包含必要的头文件
using namespace std;
int isp[202020], a[101010]; // 声明用于素数和输入数组的数组
int main() {
int n, i, j, c = 0; // 声明变量
// 使用埃拉托色尼筛选法算法初始化数组,标记数字是否为素数
for (i = 1; i <= 2e5; i++)
isp[i] = 1;
isp[1] = 0;
for (i = 1; i <= 2e5; i++) {
if (!isp[i])
continue;
for (j = i * 2; j <= 2e5; j += i)
isp[j] = 0;
}
// 输入数组的大小和数组的元素
cin >> n;
vector<int> v;
for (i = 1; i <= n; i++)
cin >> a[i];
// 查找数组中相邻元素之和为素数的对
for (i = 2; i <= n; i++)
c += isp[a[i] + a[i - 1]];
// 检查是否存在特定模式
for (i = 1; i < n; i++) {
int cc = c;
if (i > 1)
cc -= isp[a[i] + a[i - 1]];
if (i < n - 1)
cc -= isp[a[i + 1] + a[i + 2]];
if (i > 1)
cc += isp[a[i + 1] + a[i - 1]];
if (i < n - 1)
cc += isp[a[i] + a[i + 2]];
if (cc == n - 1)
v.push_back(i);
}
// 输出满足条件的特定模式的起始元素的索引,如果未找到或者找到多个位置,则输出-1
if (v.size() == 1)
cout << v[0] << '\n';
else
cout << -1 << '\n';
}
快速筛选质数笔记
3/21
__gcd 与等差数列 a[n-1] - a[0] 等于对应的数目。
#include <iostream>
#include <algorithm>
using namespace std;
long long a[100001];
int y(int a,int b)//求最大公约数
{
return b ? y(b,a%b) : a;
}
int main()
{
int n,i;
cin>>n;
for(int i=0;i<n;i++)
cin>>a[i];
sort(a,a+n);//排序
int d=a[1]-a[0];
for(int i=2;i<n;i++)
{
d=y(d,a[i]-a[i-1]);
}
if(a[n-1]==a[0])cout<<n<<endl;//考虑特殊情况
else
cout<<((a[n-1]-a[0])/d)+1<<endl;//等差数列公式
return 0;
}

bool check(int x)
{
if(sqrt(x)+floor(log(x)/log(k))-m>0) return true;
return false;
}
3/20
或 或 得 异或 a&x=b&x x = a^b
给定整数 a,b,求最小的整数 ,满足 a|x=b|x,其中|表示或运算。
so x = a^b
#include <bits/stdc++.h>
using namespace std;
int main() {
//根据|运算规则,只要有1就是1,那么只要找到两个数二进制位数中不同的位置
//,将他变成1,其余位置都是0,此时x最小
//那么不同变成1,相同变成0,不就是^嘛!
long long a, b; cin >> a >> b;
long long x = a ^ b;
cout << x << endl;
return 0;
}
还有 or ans xor
x or x = x x or 0 = x
x and x = x x and 0 = 0
x xor x = 0 x xor 0 = x
3/16
建图和树

// 包含标准的 C++ 头文件
#include <bits/stdc++.h>
// 定义别名,LL 为 long long 的缩写,Pair 为 pair<int, int> 的缩写
using LL = long long;
using Pair = std::pair<int, int>;
// 定义常量 inf 为 1'000'000'000
#define inf 1'000'000'000
// 求解函数,参数为当前测试用例的编号 Case
void solve(const int &Case) {
// 读取节点数量 n
int n;
std::cin >> n;
// 建图和树都建议按照下面的方式
// 创建一个二维向量 G,表示图的邻接表
std::vector<std::vector<int>> G(n + 1);
for (int i = 1; i < n; i++) {
// 读取边的信息 u, v,并将其加入邻接表
int u, v;
std::cin >> u >> v;
G[u].push_back(v), G[v].push_back(u);
}
// 倍增数组,用于存储每个节点向上跳 2^k 步所到达的节点
std::vector<std::array<int, 21>> F(n + 1);
// 存储节点的深度
std::vector<int> dep(n + 1);
// 深度优先搜索函数 dfs,使用 lambda 表达式定义
std::function<void(int, int)> dfs = [&](int x, int fax) {
// 预处理倍增数组 F
F[x][0] = fax;
for (int i = 1; i <= 20; i++)
F[x][i] = F[F[x][i - 1]][i - 1];
for (const auto &tox : G[x]) {
// 对每个相邻节点进行深度优先搜索
if (tox == fax)
continue;
dep[tox] = dep[x] + 1;
dfs(tox, x);
}
};
// 从根节点 1 开始深度优先搜索
dfs(1, 0);
// 求解最近公共祖先函数 glca,使用 lambda 表达式定义
auto glca = [&](int x, int y) {
if (dep[x] < dep[y])
std::swap(x, y);
// 将节点 x 跳到与节点 y 同样的深度
int d = dep[x] - dep[y];
for (int i = 20; i >= 0; i--)
if (d >> i & 1)
x = F[x][i];
if (x == y)
return x;
// 寻找最近公共祖先
for (int i = 20; i >= 0; i++) {
if (F[x][i] != F[y][i]) {
x = F[x][i];
y = F[y][i];
}
}
return F[x][0];
};
// 读取查询次数 q
int q;
std::cin >> q;
// 对每个查询进行处理
while (q--) {
int x, y;
std::cin >> x >> y;
// 输出最近公共祖先结果
std::cout << glca(x, y) << '\n';
}
}
// 主函数
int main() {
// 关闭输入输出同步,加快输入输出速度
std::ios::sync_with_stdio(false);
// 解除 cin 与 cout 的绑定,加快输入输出速度
std::cin.tie(nullptr);
std::cout.tie(nullptr);
// 设定测试用例数量为 1
int T = 1;
// 循环处理每个测试用例
for (int Case = 1; Case <= T; Case++)
solve(Case);
return 0;
}
3/13
lower_bound 和 upper_bound
两者都是定义在头文件里。用二分查找的方法在一个排好序的数组中进行查找。既然是二分,时间复杂度就是O(logN)。
基础用法
upper_bound(begin, end, value)
在从小到大的排好序的数组中,在数组的**[begin, end)区间中二分查找第一个大于**value的数,找到返回该数字的地址,没找到则返回end。
lower_bound(begin, end, value)
在从小到大的排好序的数组中,在数组的**[begin, end)区间中二分查找第一个大于等于**value的数,找到返回该数字的地址,没找到则返回end。
用greater< type >()重载
upper_bound(begin, end, value, greater<int>())
在从大到小的排好序的数组中,在数组的**[begin, end)区间中二分查找第一个小于**value的数,找到返回该数字的地址,没找到则返回end。
lower_bound(begin, end, value, greater<int>())
在从大到小的排好序的数组中,在数组的**[begin, end)区间中二分查找第一个小于等于**value的数,找到返回该数字的地址,没找到则返回end。
前两部分的代码:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
// 1.基础用法
vector<int> increasing = {1,2,3,4,5};
int pos = upper_bound(increasing.begin(), increasing.end(), 3) - increasing.begin();
cout << increasing[pos] << endl; // 4(第一个大于3的数)
pos = lower_bound(increasing.begin(), increasing.end(), 3) - increasing.begin();
cout << increasing[pos] << endl; // 3(第一个大于等于3的数)
bool res = upper_bound(increasing.begin(), increasing.end(), 5) == increasing.end();
cout << res << endl; // 1 (true,即:第一个大于5的数不存在)
// 2.greater重载
vector<int> decreasing = {5,4,3,2,1};
pos = upper_bound(decreasing.begin(), decreasing.end(), 3, greater<int>()) - decreasing.begin();
cout << decreasing[pos] << endl; // 2(第一个小于3的数)
pos = lower_bound(decreasing.begin(), decreasing.end(), 3, greater<int>()) - decreasing.begin();
cout << decreasing[pos] << endl; // 3(第一个小于等于3的数)
res = lower_bound(decreasing.begin(), decreasing.end(), 0, greater<int>()) == decreasing.end();
cout << res << endl; // 1 (true,即:第一个小于等于0的数不存在)
return 0;
}
到这里还是比较好理解的,不加greater是大于/大于等于,加上greater就是小于/小于等于。upper_bound是不带等号的,lower_bound就是带等号的。一般博客到这里就结束了,如果想要更加灵活的使用,那么请接着看。
链接:
upper_bound和lower_bound用法(史上最全) - 知乎 (zhihu.com)
3/11
DFS遍历图

BFS遍历

3/8
二维差分数组
#include<iostream>
using namespace std;
const int N = 1010;
long long a[N][N]; // 前缀和数组
long long b[N][N]; // 差分数组
// 函数:更新差分数组
void insert(int x1, int y1, int x2, int y2, int k) {
b[x1][y1] += k; // 右下侧全部加 k
b[x2 + 1][y1] -= k; // 下侧全部减去 k
b[x1][y2 + 1] -= k; // 右侧全部减去 k
b[x2 + 1][y2 + 1] += k; // 最右下侧小矩形全部加上 k
}
int main() {
int n, m, q;
cin >> n >> m >> q; // 输入前缀和数组的行列数以及循环次数
// 输入前缀和数组的值,并构建差分数组
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j]; // 输入前缀和数组
insert(i, j, i, j, a[i][j]);
// 输入差分数组,制作差分数组根本不需要再次思考,直接套用改变差分数组的函数即可
}
}
// 循环 q 次
while (q--) {
int x1, y1, x2, y2, k; // 输入 5 个变量
cin >> x1 >> y1 >> x2 >> y2 >> k;
insert(x1, y1, x2, y2, k); // 改变差分数组
}
// 将改变后差分数组的前缀和存入差分数组中
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
}
}
// 输出
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cout << b[i][j] << ' ';
}
cout << endl;
}
return 0;
}
- **函数 **
**insert**:
void insert(int x1,int y1,int x2,int y2,int k)
{
b[x1][y1]+=k;
b[x2+1][y1]-=k;
b[x1][y2+1]-=k;
b[x2+1][y2+1]+=k;
}
这个函数用来修改差分数组,实现了对矩形区域 (x1, y1) 到 (x2, y2) 的加上 k 的操作。
- **主函数 **
**main**:
- 输入前缀和数组的行数
n、列数m和循环次数q。 - 读入前缀和数组
a[][]的值,并利用insert函数构建差分数组b[][]。 - 循环
q次,读入矩形区域和对应的值k,调用insert函数修改差分数组。 - 根据差分数组的思想,计算差分数组的前缀和,得到最终的差分数组
b[][]。 - 输出最终的差分数组
b[][]。
- 差分数组的计算:
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
这个双重循环用来计算差分数组的前缀和,通过累加上方、左方的差分数组值,并减去左上角的值,得到最终的差分数组。
- 输出最终结果:
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
cout<<b[i][j]<<' ';
cout<<endl;
}
输出计算后的差分数组,即表示每个点的累加值,即最终的结果。
3/7
数据范围和对应算法

互质数的个数 4968. 互质数的个数 - AcWing题库
#include<bits/stdc++.h> // 包含标准 C++ 库的所有内容
using namespace std; // 使用 C++ 标准库的命名空间
typedef long long LL; // 定义别名 LL 代表长整型数据类型
const int mod = 998244353; // 定义取模的值
// 快速幂函数,计算 a 的 b 次幂对 mod 取模的结果
LL qmi(LL a, LL b) {
LL res = 1;
while (b) {
if (b & 1) res = res * a % mod; // 如果 b 的最低位为 1,则累乘 a
a = a * a % mod; // 更新 a 的平方,用于下一次迭代
b >>= 1; // 右移 b,相当于除以 2
}
return res; // 返回计算结果
}
int main() {
LL a, b;
cin >> a >> b; // 从标准输入流读入两个长整型数 a 和 b
if (a == 1) {
cout << 0 << endl; // 如果 a 等于 1,则直接输出 0,并返回
return 0;
}
LL res = a, x = a; // 初始化 res 为 a,并创建变量 x,其值也为 a
// 计算欧拉函数值 phi(a)
for (int i = 2; i * i <= x; i++) {
if (x % i == 0) {
while (x % i == 0) x /= i; // 不断除以质因子 i,直到无法整除为止
res = res / i * (i - 1); // 计算欧拉函数的值
}
}
if (x > 1) res = res / x * (x - 1); // 如果 x 大于 1,说明还有一个质因子,更新欧拉函数的值
// 计算最终结果并输出,即 phi(a) * a^(b-1) % mod
cout << res * qmi(a, b - 1) % mod << endl;
return 0; // 返回程序执行成功的状态码
}
- 首先,程序包含了必要的头文件
#include<bits/stdc++.h>,这个头文件通常包含了 C++ 标准库的所有内容。 - 使用
using namespace std;语句,这样可以省略代码中对std命名空间的显式声明,使得代码更加简洁。 - 程序定义了一个别名
typedef long long LL;,用于表示长整型数据类型。 - 常量
const int mod = 998244353;定义了一个取模的值,这是程序中用来取余的数值。 - 函数
LL qmi(LL a, LL b)是一个快速幂函数,用来计算mod _a_bmod的值。这里使用了二进制幂的算法来优化幂运算的时间复杂度。 main()函数是程序的入口点。
a. 首先从标准输入流中读入两个长整型数a和b。
b. 如果a等于 1,则输出 0 并返回 0。
c. 否则,程序进行数论相关的计算:
code - 初始化 `res` 为 `a`,并创建一个变量 `x`,其值也为 `a`。
- 然后,程序通过一个循环找到 `x` 的所有质因子,计算欧拉函数的值。
- 这一步的目的是计算 \( \varphi(x) \)。
- 在循环中,如果 `x` 能被 `i` 整除,就除以 `i`
- 并更新 `res` 为 \( \frac{{\text{res}}}{{i}} \times (i - 1) \),以计算欧拉函数的值。
- 如果 `x` 大于 1,表示剩下一个质因子,同样更新 `res` 以计算欧拉函数的值。
d. 最后,程序输出结果 res * qmi(a, b - 1) % mod,mod_φ_(a)×*ab−1modmod 的结果。
这段代码的目的是计算数论中的一种函数,并在取模 mod 后输出结果。
3/6
*.begin() , back(),front();
如果我们想访问容器中的第一个元素,需要使用 *d.begin() 来获取其值,因为 d.begin() 返回的是指向第一个元素的迭代器。而如果我们想访问容器中的最后一个元素,直接使用 d.back() 即可,因为 d.back() 返回的是最后一个元素的引用,不需要再使用解引用操作符。
3/5
fabs() 函数和 abs() 函数都是用于取绝对值的函数
abs() 函数:
-
- abs() 是 C/C++ 标准库函数,用于计算整数的绝对值。
- abs() 函数接受整数参数,返回整数类型的绝对值。
- 示例:
int result = abs(-5); // result 的值为 5
- fabs() 函数:
- fabs() 是 math.h(或cmath)中的函数,用于计算浮点数的绝对值。
- fabs() 函数接受浮点数参数,返回浮点数类型的绝对值。
- 示例:
double result = fabs(-3.14); // result 的值为 3.14
ceil 和 floor
double roundedNum = floor(num);
double roundedNum = ceil(num);
ceil(x)函数返回不小于 x 的最小整数,即向上取整。无论 x 是正数还是负数,ceil函数都会返回大于或等于 x 的最小整数。例如,ceil(3.14)将返回 4,ceil(-2.7)将返回 -2。floor(x)函数返回不大于 x 的最大整数,即向下取整。无论 x 是正数还是负数,floor函数都会返回小于或等于 x 的最大整数。例如,floor(3.14)将返回 3,floor(-2.7)将返回 -3。
floor 下取整 ceil 上取整 为 <math,h>

n+x-1/x 向下取整
cmath的log() log2() log10();
另外如果自定义以m为底,求log n的值
需要double a=log(n)/log(m);
(1)以e为底的对数
比如:以e为底5的对数ln5 使用log(5)(2)以2为底的对数
比如:以2为底10的对数log210 使用log2(10)(3)以10为底的对数
比如:以10为底100的对数log10100 使用log10(100)(4)exp(n)值为e^n次方
(5)以n为底m的对数
我们就要使用换底公式:lognm = ln m / ln n
也就是:log(m) / log(n)
#include <iostream>
#include <cmath>
#include <algorithm>
#include <cstdlib>
using namespace std;
int main()
{
int n = 23333333;
for(int i = 1;i<=n;i++)
{
double a = i*1.0/n;
double b = (n-i)*1.0/n;
double ans = 0;
ans -= a * log2(a) * i + b * log2(b) * (n-i);
if(abs(ans - 11625907.5798)<0.0001)
{
cout<<i<<endl;
break;
}
}
return 0;
}
string::npos 的值是 size_t 类型的最大可能值,在大多数情况下等于 -1。
3/4
set 默认排序小~大
默认set容器默认排序规则为从小到大
3/3
lowbit快速求出

1/21
KMP
//本题考查对next数组含义的理解
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+100;
char T[N],S[N];//T是文本串,S是模式串
int nex[N];//next数组表示失配时模式串指针移动到什么位置
int n,n1;//n为文本串长度,n1为模式串长度
void get_next(int n)//对文本串T求其next数组,获取最短循环节的长度
{
nex[0]=nex[1]=0;
for(int i=2,j=0;i<=n;i++)
{
while(j&&T[i]!=T[j+1])j=nex[j];
if(T[i]==T[j+1])j++;
nex[i]=j;
}
}
int KMP(int T_length,int S_length)//在文本串T中匹配模式串S,记录匹配成功的次数
{
int ans=0;
for(int i=1,j=0;i<=T_length;i++)
{
while(j&&T[i]!=S[j+1])j=nex[j];
if(T[i]==S[j+1])j++;
if(j==S_length)ans++;
}
if(n%ans==0)return ans;
//若匹配成功的次数能被文本串的长度整除,说明该文本串可以由ans个模式串构成
else return 1;//不能整除,说明该模式串(循环节)不能构成原文本串,只能返回1
}
int main()
{
cin>>T+1;//输入文本串,下标从1开始
n=strlen(T+1);//计算文本串长度
get_next(n);//对文本串求next数组
//若T=ababab,则next数组为 0 0 1 2 3 4,开头有两个0,说明最短循环节长度为2
n1=n-nex[n];//求最短循环节的长度
for(int i=1;i<=n1;i++)S[i]=T[i];//将最短循环节作为模式串
int ans=KMP(n,n1);//在文本串中匹配模式串,记录匹配成功的次数
cout<<ans<<endl;
return 0;
}
#include<bits/stdc++.h>
using namespace std;//KMP
const int N=1e6+9;
char s[N];
int nex[N];//主串S
main()
{
cin>>s+1;
int n=strlen(s+1);
nex[0]=nex[1]=0;
for(int i=2,j=0;i<=n;i++)//取nex数组
{
while(j&&s[i]!=s[j+1]) j=nex[i];
if(s[i]==s[j+1])j++;
nex[i]=j;
}
int t=n-nex[n];
if(t!=n&&n%t==0) cout<<n/t;
else cout<<1;
}
1/9
路径树形DP
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int N = 2005;
vector<int> e[N], t; // e 存储树的边,t 用于存储路径中的点。
struct asdf {
vector<int> vec; // vec 表示路径中的点。
LL val; // val 表示该路径产生的价值。
};
vector<asdf> w[N]; // w 存储每个点到根节点路径上的所有路径和价值。
LL dp[N]; // dp 数组表示以 i 号节点为根的子树中,所能获得的最大价值。
int n, m, k, dep[N] = { 1 }, f[N]; // dep 数组表示每个节点的深度,f 数组表示每个节点的父节点编号。
void dfs(int u) // u 表示当前节点编号。
{
for (auto v : e[u]) // 遍历 u 的子节点 v。
{
dfs(v); // 递归处理以 v 为根的子树。
dp[u] += dp[v]; // 将以 v 为根的子树所能获得的价值累加到以 u 为根的子树中。
}
for (auto t : w[u]) // 遍历 u 到根节点路径上的所有路径。
{
LL sum = dp[u]; // sum 表示除了当前路径之外的所有价值之和。
for (auto nw : t.vec) // 遍历当前路径上的所有节点。
{
sum -= dp[nw]; // 将当前节点的贡献值从 sum 中减去。
for (auto v : e[nw]) sum += dp[v]; // 将以该节点为根的子树所能获得的价值累加到 sum 中。
}
dp[u] = max(dp[u], sum + t.val); // 更新以 u 为根的子树所能获得的最大价值。
}
}
int main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> n >> m;
for (int i = 2; i <= n; ++i)
{
cin >> f[i];
e[f[i]].push_back(i);
dep[i] = dep[f[i]] + 1; // 计算每个节点的深度。
}
for (int i = 1, x, y; i <= m; ++i)
{
LL val;
cin >> x >> y >> val;
t.clear();
while (x != y) // 计算 x 到 y 的路径。
{
if (dep[x] > dep[y]) t.push_back(x), x = f[x];
else t.push_back(y), y = f[y];
}
t.push_back(x);
w[x].push_back({ t,val }); // 将路径和价值存入 w 数组中。
}
dfs(1); // 从根节点开始 dfs。
cout << dp[1]; // 最后输出以根节点为根的子树所能获得的最大价值。
return 0;
}
第二种
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int N = 2005;
vector<int> e[N]; // e 存储树的边。
struct asdf {
int x; // x 表示路径中的节点编号。
LL val; // val 表示该路径产生的价值。
};
vector<asdf> w[N]; // w 存储每个节点到根节点路径上的所有路径和价值。
int n, m, dep[N]; // dep 数组表示每个节点的深度。
LL dp[N][N]; // dp[i][j] 表示以 i 号节点为根的子树中,深度为 j 的节点所能获得的最小代价。
void dfs(int u) // u 表示当前节点编号。
{
LL sum = 0; // sum 表示除了当前节点子树中的所有代价之和。
for (int i = 1; i <= dep[u]; ++i) dp[u][i] = 1e18; // 初始化 dp 数组。
for (auto v : e[u]) // 遍历 u 的子节点 v。
{
dfs(v); // 递归处理以 v 为根的子树。
sum += dp[v][dep[u] + 1]; // 将以 v 为根的子树的代价累加到 sum 中。
if (sum >= 1e18) // 如果 sum 超过了 long long 类型的最大值,则直接输出 -1 并退出程序。
{
cout << -1;
exit(0);
}
for (int i = 1; i <= dep[u]; ++i) // 更新 dp 数组。
dp[u][i] = min(dp[u][i], dp[v][i] - dp[v][dep[u] + 1]); // 将以 v 为根的子树中深度为 i 的节点所能获得的最小代价减去其子树中深度为 dep[u]+1 的节点所能获得的最小代价,更新到以 u 为根的子树中深度为 i 的节点所能获得的最小代价中。
}
for (int i = 1; i <= dep[u]; ++i) dp[u][i] += sum; // 将 sum 加到所有深度为 i 的节点所能获得的最小代价中。
for (auto v : w[u]) // 遍历 u 到根节点路径上的所有路径。
dp[u][dep[v.x]] = min(dp[u][dep[v.x]], sum + v.val); // 将当前路径的代价加上 sum,更新到以 u 为根的子树中深度为 dep[v.x] 的节点所能获得的最小代价中。
for (int i = 2; i <= dep[u]; ++i) dp[u][i] = min(dp[u][i], dp[u][i - 1]); // 将深度大于 1 的节点的最小代价更新为前缀最小值。
}
int main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin >> n >> m;
dep[1] = 1; // 根节点的深度为 1。
for (int i = 2; i <= n; ++i)
{
int f;
cin >> f;
e[f].push_back(i); // 加入边。
dep[i] = dep[f] + 1; // 计算每个节点的深度。
}
for (int i = 1; i <= m; ++i)
{
int x, y;
LL val;
cin >> x >> y >> val;
if (dep[x] > dep[y]) swap(x, y); // 确保 x 的深度不大于 y 的深度。
w[y].push_back({ x,val }); // 将路径和价值存入 w 数组中。
}
dfs(1); // 从根节点开始 dfs。
cout << dp[1][1]; // 最后输出以根节点为根的子树中深度为 1 的节点所能获得的最小代价。
return 0;
}
1/6
背包总结:
01
物品 背包倒序
// 先遍历物品 再背包倒序
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
完全背包
物品 背包正序
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
多重背包
普通法
//先遍历物品 再背包倒序
for(int i=1;i<=n;i++)
{
int w,v,s;
cin>>w>>v>>s;
while(s--)
{
for(int j = m;j>=w;j--)
{
dp[j] = max(dp[j],dp[j-w]+v);
}
}
}
// 遍历每个物品
for(int i = 1; i <= n; ++i) {
ll v, w, s;
cin >> v >> w >> s;
// 处理多重背包问题
for(int k = 1; k <= s; s -= k, k += k) {
for(int j = m; j >= k * v; --j) {
dp[j] = max(dp[j], dp[j - k * v] + k * w);
}
}
// 处理剩余数量小于k的情况
for(int j = m; j >= s * v; --j) {
dp[j] = max(dp[j], dp[j - s * v] + s * w);
}
}
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
1/5
动态规划 01背包 模板
dp[j] 能装满背包为 j 的最大价值先遍历物品,
在遍历背包,组合数。
反过来,为排列数
#include<iostream>
using namespace std;
const int N = 110, V = 1010; // N表示物品个数,V表示背包容量
using ll = long long;
int dp[N][V]; // dp[i][j]表示前i个物品在不超过j的容量限制下能够获得的最大价值
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 提高cin, cout的速度
int nn, vv;
cin >> nn >> vv; // 输入物品个数和背包容量
for (int i = 1; i <= nn; ++i) { // 遍历每个物品
int w, v;
cin >> w >> v; // 物品i的重量和价值
for (int j = 1; j <= vv; ++j) { // 遍历每个重量限制
if (j >= w) { // 如果当前背包容量可以放下物品i
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w] + v); // 取放和不放两种情况下的最大价值
} else { // 如果放不下物品i
dp[i][j] = dp[i - 1][j]; // 不放物品i,背包容量限制不变
}
}
}
cout << dp[nn][vv]; // 输出前nn个物品在容量限制为vv时的最大价值
return 0;
}
首先再回顾一下01背包的核心代码
先物品,背包倒序遍历
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
我们知道01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
完全背包 正反都可以
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
先遍历背包在遍历物品,代码如下:
// 先遍历背包,再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
for(int i = 0; i < weight.size(); i++) { // 遍历物品
if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
cout << endl;
}
多重背包模板4
首先,通过输入获取物品的数量n和背包容量m。
然后,对于每个物品,依次输入其重量w、价值v和数量s。
接下来,通过两重循环来处理多重背包问题。外层循环遍历每个物品,内层循环遍历该物品的数量。
在内层循环中,使用逆序的方式遍历背包容量,从大到小更新dp数组。具体的更新规则为
dp[j] = max(dp[j], dp[j - w] + v),表示在背包容量为j的情况下,可以选择不同数量的该物品来获得最大的价值。最后,输出dp[m]即为能够在背包容量为m的情况下获得的最大价值。
#include<bits/stdc++.h>
using namespace std;
int n, m, dp[1000];
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n >> m;
// 遍历每个物品
for (int i = 1; i <= n; i++) {
int w, v, s;
cin >> w >> v >> s;
// 对于每个物品,遍历其数量
while (s--) {
// 在背包容量范围内,从大到小遍历背包容量
for (int j = m; j >= w; j--) {
dp[j] = max(dp[j], dp[j - w] + v);
}
}
}
cout << dp[m];
return 0;
}
多重背包优化 二进制优化 n,log(s),v;
首先,通过输入获取物品的数量n和背包容量m。
然后,对于每个物品,依次输入其价值v、重量w和数量s。
接下来,使用两重循环来处理多重背包问题。外层循环遍历每个物品,内层循环处理该物品的数量。
在内层循环中,使用两种策略来更新dp数组。
第一种策略是处理数量k,通过逐渐增加选择物品的数量,如果剩余数量小于等于k,则选择剩余数量的物品。具体的更新规则为
dp[j] = max(dp[j], dp[j - k * v] + k * w)。表示在背包容量为j的情况下,可以选择多个数量为k的该物品来获得最大的价值。第二种策略是处理剩余数量小于k的情况,即将剩余数量的物品全部选择。具体的更新规则为
dp[j] = max(dp[j], dp[j - s * v] + s * w)。最后,输出dp[m]即为能够在背包容量为m的情况下获得的最大价值。
#include<iostream>
using namespace std;
using ll = long long ;
const int N = 1e3+10,M=2e4+7;
ll dp[M];
int main() {
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n, m;
cin >> n >> m;
// 遍历每个物品
for(int i = 1; i <= n; ++i) {
ll v, w, s;
cin >> v >> w >> s;
// 处理多重背包问题
for(int k = 1; k <= s; s -= k, k += k) {
for(int j = m; j >= k * v; --j) {
dp[j] = max(dp[j], dp[j - k * v] + k * w);
}
}
// 处理剩余数量小于k的情况
for(int j = m; j >= s * v; --j) {
dp[j] = max(dp[j], dp[j - s * v] + s * w);
}
}
cout << dp[m];
return 0;
}
二维费用背包
首先,通过输入获取物品的数量n和背包的两个费用维度V和M。
然后,对于每个物品,依次输入其对应的费用v、m和价值w。
接下来,在内层循环中,使用一种策略来更新dp数组。具体地,在每个物品的每个数量上,使用完全背包策略来更新dp数组,即
dp[j][z]=max(dp[j][z],dp[j-v][z-m]+w)。表示在背包容量为j,第一个费用为z,第二个费用为(k * m)的情况下,选择该物品所获得的最大价值。最终,输出dp[V][M]即为能够在背包容量为V,第一个费用为M,第二个费用为0的情况下获得的最大价值。
#include<bits/stdc++.h>
using namespace std;
int n,V,M,dp[110][110];
// dp[i][j] 表示在容量为 i,第一个费用为 j,第二个费用为 k 的情况下能获得的最大价值
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n>>V>>M;
// 遍历每个物品
for(int i=1;i<=n;i++)
{
int v,m,w;
cin>>v>>m>>w;
// 对于每个物品,使用完全背包策略更新dp数组
for(int j=V;j>=v;j--)
{
for(int z=M;z>=m;z--)
{
dp[j][z]=max(dp[j][z],dp[j-v][z-m]+w);
}
}
}
cout<<dp[V][M];
return 0;
}
分组背包
首先,通过输入获取物品组的数量n和背包容量V。
然后,对于每个物品组,依次输入其物品数量s,以及每个物品对应的费用w和价值v。
接下来,在内层循环中,使用一种策略来更新dp数组。具体地,在每个物品组的每个物品上,使用多重背包的策略来更新dp数组。在每个物品上,通过逐渐增加选择该物品的数量,如果剩余容量大于等于k * w,则选择k个该物品。具体的更新规则为
dp[j] = max(dp[j], dp[j - k * w] + k * v)。表示在背包容量为j的情况下,可以选择多个数量为k的该物品来获得最大的价值。最后,输出dp[V]即为能够在背包容量为V的情况下获得的最大价值。
#include <iostream>
using namespace std;
using ll = long long ;
const int N = 150;
ll dp[N][N];
int main() {
int n, V;
cin >> n >> V;
// 遍历每个物品
for(int i = 1; i <= n; ++i) {
int s;
cin >> s;
// 对于每个物品的每个数量,进行更新
while(s--) {
ll w, v;
cin >> w >> v;
// 更新dp数组
for(int j = w; j <= V; ++j) {
dp[i][j] = max(dp[i][j], dp[i-1][j-w] + v);
}
}
// 处理剩余数量的情况
for(int j = 0; j <= V; ++j) {
dp[i][j] = max(dp[i][j], dp[i-1][j]);
}
}
cout << dp[n][V];
return 0;
}
1/4
LIS(最长上升子序列)
模板
#include <iostream>
using namespace std;
#define endl '\n';
const int N = 1e3 + 9;
int a[N], dp[N];
int main()
{
int n;
cin >> n;
// 输入数组a
for(int i = 1; i <= n; ++i)
cin >> a[i];
// 计算最长递增子序列长度,dp[i]表示以第i个元素结尾的最长递增子序列长度
int ans = 0;
for(int i = 1; i <= n; ++i)
{
dp[i] = 1;
for(int j = 1; j < i; ++j)
if(a[i] > a[j]) dp[i] = max(dp[i], dp[j] + 1); // 找到一个最大值。
ans = max(ans, dp[i]); // 更新最长递增子序列长度
}
cout << ans << endl;
return 0;
}
LIS优化版
这段代码的重点是使用动态规划算法求解最长上升子序列(LIS)问题。在遍历数组
a的过程中,通过维护一个dp数组,实现了时间复杂度为 O_(_n_log_n) 的 LIS 算法。具体来说,使用
dp[i]表示以a[i]结尾的最长上升子序列的长度,然后根据当前元素和之前元素的大小关系,不断更新dp数组的值,最终返回dp数组中的最大值即为最长上升子序列的长度。在更新
dp数组的过程中,使用了二分查找算法,在已知有序数组中查找第一个大于等于某个给定值的位置,从而保证了dp[0...len-1]是一个递增的序列,也就是说,其中包含了所有可能的上升子序列。因此,这段代码的重点在于理解动态规划算法和二分查找算法的原理,并掌握如何利用它们解决最长上升子序列问题。同时,通过输出每次循环后
dp数组的值,加深对算法实现的理解和调试能力。
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 1010;
int dp[maxn];
int a[maxn];
int main()
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
int len = 1;
dp[1] = a[1];
for (int i = 2; i <= n; i++)
{
if (dp[len] < a[i])
{
dp[++len] = a[i];
}
else {
//在a[i]<dp[len]时用a[i]覆盖dp之前的使其尽可能的小保证上升子序列尽可能的长
int pos = lower_bound(dp, dp + len, a[i]) - dp;
dp[pos] = a[i];//dp[i]=x在x之前包括x有三个最长上升子序列
}
cout << "第" << i - 1 << "次" << endl;
for (int i = 1; i <= n; ++i)
{
cout << dp[i]<<" ";
}
cout <<endl<<"--------------------------------" << endl;
}
cout << len << endl;
return 0;
}
LIS二分优化
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e6+10;
int f[N],n=1,b[N];
int main(){
cin>>n;
for(int i = 1;i<=n;++i)cin>>b[i];
int sum=0;
for(int i=1;i<=n;i++){
if(f[sum]<b[i]){//特判最长长度增加的情况
sum++;
f[sum]=b[i];
continue;
}
int l=0,r=sum;
while(l+1<r){
int mid=(l+r)/2;
if(f[mid]>=b[i])
r=mid;
else
l=mid;
}
f[r]=min(f[r],b[i]);//更新f[l+1]的值
}
cout<<sum;
return 0;
}
LCS(最长公共子序列)
#include<iostream>
using namespace std;
const int N = 1e3+9;
int n,m,a[N],b[N],dp[N][N];
int main()
{
int n,m; // 初始化变量 n 和 m
cin>>n>>m; // 输入 n 和 m 的值
// 输入数组 a
for(int i = 1;i<=n;++i)
cin>>a[i];
// 输入数组 b
for(int i = 1;i<=m;++i)
cin>>b[i];
// 动态规划循环计算最长公共子序列
for(int i = 1;i<=n;++i)
{
for(int j = 1;j<=m;++j)
{
if(a[i]==b[j])
dp[i][j] = dp[i-1][j-1]+1; // 如果元素相等,则将 LCS 值加一
else
dp[i][j] = max(dp[i-1][j],dp[i][j-1]); // 如果元素不相等,则取前面的 LCS 值的最大值
}
}
// 输出最长公共子序列的长度
cout<<dp[n][m]<<endl;
return 0;
}
输出子序列

1/2
背包模板
#include <iostream>
using namespace std;
const int N = 1e6 + 10; // 定义物品数量上限
int Time[110]; // 定义花费数组
int profit[110]; // 定义价值数组
int dp[N]; // 定义动态规划数组
int main()
{
int M, N, K; // 定义可用于购买物品的钱数、物品数量、新增的K值
cin >> M >> N; // 读入可用于购买物品的钱数和物品数量
for (int i = 1; i <= N; ++i)
cin >> Time[i] >> profit[i]; // 读入每种物品的花费和价值
cin >> K; // 读入新增的K值
M = M + K; // 将可用于购买物品的钱数加上K
for (int i = 1; i <= N; ++i)
Time[i] = Time[i] + K; // 将所有物品的花费加上K
// 进行动态规划的计算
for (int i = 1; i <= M; ++i) // 遍历不同钱数下的最大价值
{
dp[i] = dp[i - 1]; // 初始化dp[i]
for (int j = 1; j <= N; ++j) // 遍历每种物品
{
// 计算选择该物品和不选择该物品两种情况下能够获得的价值,取较大值作为dp[i]的值
dp[i] = max(dp[i], dp[i - Time[j]] + profit[j]);
}
}
cout << dp[M] << endl; // 输出最大价值
return 0;
}
2023年结束啦
12/31
翻转:旋转
代码中定义了两个函数
flip和rotate,分别实现了左右翻转和逆时针旋转90度的功能。
flip函数用于实现左右翻转:
- 遍历向量
a中的每一行,使用双指针进行左右翻转操作。- 左指针
j从行的开头向右移动,右指针k从行的末尾向左移动,交换两个指针所指向的字符,实现左右翻转。- 返回翻转后的向量
a。
rotate函数用于实现逆时针旋转90度:
- 首先调用
flip函数对向量a进行左右翻转。- 然后遍历向量
a中的每一行,只遍历上半部分的元素,避免重复交换。- 对于每个位置
(i, j),交换a[i][j]和a[j][i]的值,实现逆时针旋转90度。- 返回旋转后的向量
a。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
int n;
vector<string> a, b;
vector<string> flip(vector<string> a) // 左右翻转
{
for (int i = 0; i < n; i ++ )
for (int j = 0, k = n - 1; j < k; j ++, k -- )
swap(a[i][j], a[i][k]);
return a;
}
vector<string> rotate(vector<string> a) // 逆时针旋转90度
{
a = flip(a);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < i; j ++ )
swap(a[i][j], a[j][i]);
return a;
}
bool check()
{
for (int i = 0; i < 4; i ++ ) // 进行四次旋转
{
a = rotate(a); // 逆时针旋转90度
if (a == b) return true; // 如果旋转后的向量与目标向量相等,则返回true
}
a = flip(a); // 进行左右翻转
for (int i = 0; i < 4; i ++ ) // 进行四次旋转
{
a = rotate(a); // 逆时针旋转90度
if (a == b) return true; // 如果旋转后的向量与目标向量相等,则返回true
}
return false; // 如果没有找到匹配的旋转方式,则返回false
}
int main()
{
cin >> n; // 输入矩阵的大小 n
a = b = vector<string>(n); // 定义两个大小为 n 的字符串向量 a 和 b
for (int i = 0; i < n; i ++ ) cin >> a[i]; // 输入矩阵 a 的每一行
for (int i = 0; i < n; i ++ ) cin >> b[i]; // 输入矩阵 b 的每一行
if (check()) cout << "Yes" << endl; // 检查是否存在旋转后与目标矩阵相等的情况,如果存在则输出 "Yes"
else cout << "No" << endl; // 如果不存在,则输出 "No"
return 0;
}
12/29
DFS - jgk模板
#include <iostream>
using namespace std;
const int N = 110; // 定义常量N为110,表示数组大小
int nxy[][2] = {1, 0, -1, 0, 0, 1, 0, -1}; // 方向数组,用于表示上下左右四个方向移动
int map1[N][N]; // 地图数组,存储地图信息
int vis[N][N] = {0}; // 访问标记数组,用于记录已经访问过的位置
long long ans; // 存储答案
long long sum; // 存储当前连通块的和
int n, m; // 输入的行数和列数
// DFS遍历连通块
void dfs(int x, int y)
{
if (x < 1 || x > n || y < 1 || y > m || map1[x][y] == 0 || vis[x][y] == 1)
return; // 边界判断和访问判断
vis[x][y] = 1; // 标记当前位置为已访问
sum += map1[x][y]; // 累加当前位置的值
for (int i = 0; i < 4; i++)
{
int nx = x + nxy[i][0]; // 计算下一个位置的x坐标
int ny = y + nxy[i][1]; // 计算下一个位置的y坐标
dfs(nx, ny); // 递归遍历下一个位置
}
}
int main()
{
// 输入行数和列数
cin >> n >> m;
// 输入地图信息
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
cin >> map1[i][j];
// 遍历每一个位置
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
if (map1[i][j] != 0)
{
sum = 0; // 初始化连通块的和
dfs(i, j); // DFS遍历连通块
}
ans = ans > sum ? ans : sum; // 更新答案
}
}
// 输出答案
cout << ans << endl;
return 0;
}
12/28
floor 下取整 ceil 上取整 为 <math,h>

n+x-1/x 向下取整
12/21
离散化模板
#include <bits/stdc++.h> // 包含常用的标准库头文件
using namespace std;
const int N = 1e5 + 9; // 定义常量N,表示数组a的最大长度
int a[N]; // 声明整型数组a,用于存储输入的原始数据
vector<int> L; // 声明整型向量L,作为离散化后的数组
// 获取元素在离散化后的数组中的下标
int getidx(int x) {
return lower_bound(L.begin(), L.end(), x) - L.begin(); // 使用lower_bound函数查找插入位置,计算下标并返回
}
int main() {
int n;
cin >> n; // 从标准输入读入一个整数n,表示数组的长度
for (int i = 1; i <= n; ++i)
cin >> a[i]; // 使用循环,从标准输入读入n个整数,并将其存储到数组a中
for (int i = 1; i <= n; ++i)
L.push_back(a[i]); // 使用循环,将数组a的元素添加到向量L中
sort(L.begin(), L.end()); // 对向量L进行排序,使其变为有序数组
L.erase(unique(L.begin(), L.end()), L.end()); // 使用erase函数去除向量L中的重复元素
cout << "离散化数组为:"; // 输出离散化后的数组L中的元素
for (const auto& i : L)
cout << i << ' ';
cout << '\n'; // 换行输出
int val;
cin >> val; // 从标准输入读入一个整数val
cout << getidx(val) << '\n'; // 调用getidx函数,计算val在离散化数组L中的下标,并输出结果
return 0;
}
12/20
前缀和模板
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5 + 7;
ll a[N];
ll prefix[N];
void solve()
{
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; i++)
cin >> a[i];
sort(a + 1, a + n + 1);
for (int i = 1; i <= n; i++)
prefix[i] = prefix[i - 1] + a[i];
ll ans = 0;
for (int i = 0; i <= k; i++)
{ // i次删前面,k-i删后面
ans = max(ans, prefix[n - k + i] - prefix[2 * i]);
}
cout << ans << endl;
}
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int t;
cin >> t;
while (t--)
solve();
return 0;
}
差分模板
15.肖恩的投球游戏 - 蓝桥云课 (lanqiao.cn)
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int b[N];
int main()
{
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n, q;
cin >> n >> q;
for (int i = 1; i <= n; ++i)
cin >> a[i];
for (int i = 1; i <= n; ++i)
b[i] = a[i] - a[i - 1];
while (q--)
{
int l, r, c;
cin >> l >> r >> c;
b[l] += c;
b[r + 1] -= c;
}
for (int i = 1; i <= n; ++i)
{
a[i] = a[i - 1] + b[i];
}
for (int i = 1; i <= n; ++i)
cout << a[i] << " ";
cout << endl;
return 0;
}
二维差分
#include <stdio.h>
int arr[1000][1000]; // 原二维数组
int d[1001][1001]; // 差分数组
// 插入操作,向差分数组中插入差分值
void insert(int x1, int y1, int x2, int y2, int c)
{
d[x1][y1] += c; // 左上角增加 c
d[x2 + 1][y1] -= c; // 右上角减去 c
d[x1][y2 + 1] -= c; // 左下角减去 c
d[x2 + 1][y2 + 1] += c; // 右下角增加 c
}
int main()
{
int n = 0, m = 0, q = 0; // n 表示行数,m 表示列数,q 表示操作次数
scanf("%d %d %d", &n, &m, &q);
int i = 0;
int j = 0;
// 输入整数矩阵,并计算二维差分
for (i = 0; i < n; i++)
{
for (j = 0; j < m; j++)
{
scanf("%d", &arr[i][j]);
insert(i, j, i, j, arr[i][j]); // 将原始值插入差分数组中
}
}
// 进行 q 次操作
while (q--)
{
int x1 = 0, y1 = 0, x2 = 0, y2 = 0;
int c = 0;
scanf("%d %d %d %d %d", &x1, &y1, &x2, &y2, &c); // 输入操作参数
insert(x1, y1, x2, y2, c); // 对差分数组进行插入操作
}
// 计算二维差分的前缀和,即原二维数组 arr
arr[0][0] = d[0][0];
for (j = 1; j < m; j++)
{
arr[0][j] = arr[0][j - 1] + d[0][j]; // 计算第一行的前缀和
}
for (i = 1; i < n; i++)
{
arr[i][0] = arr[i - 1][0] + d[i][0]; // 计算第一列的前缀和
}
for (i = 1; i < n; i++)
{
for (j = 1; j < m; j++)
{
arr[i][j] = arr[i - 1][j] + arr[i][j - 1] - arr[i - 1][j - 1] + d[i][j]; // 计算其他位置的前缀和
}
}
// 输出
for (i = 0; i < n; i++)
{
for (j = 0; j < m; j++)
{
printf("%d ", arr[i][j]); // 输出二维数组的值
}
printf("\n");
}
return 0;
}
12/9
accumulate是numeric库中的一个函数
accumulate是numeric库中的一个函数,主要用来对指定范围内元素求和,但也自行指定一些其他操作,如范围内所有元素相乘、相除等。
使用前需要引入相应的头文件。
#include
函数共有四个参数,其中前三个为必须,第四个为非必需。
若不指定第四个参数,则默认对范围内的元素进行累加操作。
accumulate(起始迭代器, 结束迭代器, 初始值, 自定义操作函数)
12/8
初始化:
全局初始化为 0 局部初始话为 随机
C++配置环境
-std=gnu11 -std=gnu14 -std=gnu17 -std=gnu20
覆盖区间问题 auto [l, r] :
auto [l, r] 是 C++17 的一种语法,称为结构化绑定(Structured Binding),它可以方便地将一个结构体或者数组中的元素赋值给多个变量。
在这里,[l, r] 表示一个包含两个元素的数组或者 pair,而 auto 关键字会让编译器自动推断变量类型,将左端点存储在变量 l 中,将右端点存储在变量 r 中。因此,在循环体中可以直接使用 l 和 r 这两个变量来访问当前区间的左右端点。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int n, len; // 区间个数和总长度
int pos[100010], s[100010]; // 区间位置和长度
bool check(int t)
{
vector<pair<int,int>> v; // 存储符合条件的区间的左右端点
// 遍历每个区间,根据条件将符合要求的区间的左右端点添加到 v 中
for(int i = 1; i <= n; i++)
{
if(s[i] > t) continue; // 如果长度大于 t,则跳过该区间
int ll = pos[i] - (t - s[i]); // 左端点为 pos[i] - (t - s[i])
int rr = pos[i] + (t - s[i]); // 右端点为 pos[i] + (t - s[i])
v.push_back({ll, rr}); // 将左右端点添加到 v 中
}
sort(v.begin(), v.end()); // 对 v 中的区间按照左端点进行排序
int now = 0; // 当前已经覆盖到的最远位置
// 遍历排序后的区间,检查是否能够覆盖到整个长度 len
for(auto [l,r] : v)
{
if(now + 1 >= l)
now = max(now, r); // 若当前位置已经大于等于 l,则更新最远位置为 r
else
return false; // 否则无法覆盖到整个长度 len,返回 false
}
if(now >= len)
return true; // 若最远位置已经大于等于长度 len,则返回 true
else
return false; // 否则返回 false
}
int main()
{
int res = -1; // 最终结果,默认为 -1
cin >> n >> len; // 输入区间个数和总长度
for(LL i = 1; i <= n; i++)
{
cin >> pos[i] >> s[i]; // 输入每个区间的位置和长度
}
int l = 0, r = 2e9; // 二分查找的左右边界
while(l <= r)
{
int mid = (r - l) / 2 + l; // 计算中间位置
if(check(mid)) // 判断是否满足条件
{
res = mid; // 更新结果为当前中间位置
r = mid - 1; // 缩小右边界
}
else
{
l = mid + 1; // 缩小左边界
}
}
cout << res << endl; // 输出结果
return 0;
}
12/7
C++进制转化的库函数
总结
n转十
char a[] = "目标数";
char *b ;
cout<<strtol(a,&b,n);
cout<<b<<endl;
十转n
int a = 目标数;
char b[100];
itoa(a,b,n);
cout<<b<<endl;
printf("%05o\n",35); //按八进制格式输出,保留5位高位补零
printf("%03d\n",35); //按十进制格式输出,保留3位高位补零
printf("%05x\n",35); //按十六进制格式输出,保留5位高位补零
cout << "36的8进制:" << std::oct << 36 << endl;
cout << "36的10进制" << std::dec << 36 << endl;
cout << "36的16进制:" << std::hex << 36 << endl;
cout << "36的2进制: " << bitset<8>(36) << endl;
1.strtol 函数:
它的功能是将一个任意1-36进制数转化为10进制数,传入字符串,返回是long int型。
函数为long int strtol(const char *nptr, char **endptr, int base)
base是被转化的数的进制,非法字符会赋值给endptr,nptr是要转化的字符,例如:
char buffer[20]="10379cend3";
char *stop;
printf("%d\n",strtol(buffer, &stop, 8));
printf("%s\n", stop);
输出结果:
543
9cend$3 //对八进制而言,‘9’是非法的,所以从该字符往后都赋给endptr(stop)
将一个8进制转化为10进制,读取1037(对应的10进制为543),其他后面的为非法字符,转化结果以long int型输出来。
另外,如果base为0,且字符串不是以0x(或者0X)开头,则按十进制进行转化。如果base为0或者16,并且字符串以0x(或者0X)开头,那么,x(或者X)被忽略,字符串按16进制转化。如果base不等于0和16,并且字符串以0x(或者0X)开头,那么x被视为非法字符。
最后,需要说明的是,对于nptr指向的字符串,其开头和结尾处的空格被忽视,字符串中间的空格被视为非法字符。
2.itoa函数:
它的功能是将一个10进制的数转化为n进制的值、其返回值为char型。(和上面的strtol效果相反)
例如:itoa(num, str, 2); num是一个int型的,是要转化的10进制数,str是转化结果,后面的值为目标进制。
#include<cstdlib>
#include<cstdio>
int main()
{
int num = 10;
char str[100];
char *s; //也可以
itoa(num, str, 2);
printf("%s\n", str); printf("%s\n", s);
return 0;
}
输出结果:
1010
3.指定进制的输出
C语言:
printf("%05o\n",35); //按八进制格式输出,保留5位高位补零
printf("%03d\n",35); //按十进制格式输出,保留3位高位补零
printf("%05x\n",35); //按十六进制格式输出,保留5位高位补零
运行结果:
00043
035
00023
C++:
std::bitset(转2进制),std::oct(转8进制),std::dec (转10进制),std::hex(转16进制)。
#include <bitset>
#include <iostream>
using namespace std;
int main()
{
cout << "36的8进制:" << std::oct << 36 << endl;
cout << "36的10进制" << std::dec << 36 << endl;
cout << "36的16进制:" << std::hex << 36 << endl;
cout << "36的2进制: " << bitset<8>(36) << endl;
return 0;
}
运行结果:
36的8进制:44
36的10进制36
36的16进制:24
36的2进制: 00100100
strcmp()
strcmp() 用来比较字符串(区分大小写),其原型为:
intstrcmp(const char*s1, const char *s2);
若参数s1 和s2 字符串相同则返回0。s1 若大于s2 则返回大于0 的值。s1 若小于s2 则返回小于0 的值。
compare()
说明string类型的字符串是可以拿来直接比较的。
当然在查找过程中也发现string类型的字符串比较还可以用compare()函数来进行。
12/6
memset简介
【注意事项】
1.二维整型数组直接利用 memset() 函数初始化时,只能初始化为 0 或 -1 ,否则将会被设为随机值。
2.二维 char 型数组利用 memset() 函数初始化时不受限制,可以初始化任意字符。
#include<stdio.h>
#include<string.h>
int main()
{
int a[10][10];
memset(a,0,sizeof(a));
for(int i = 0;i < 10;i++)
{
for(int j = 0;j < 10;j++)
printf("%d ",a[i][j]);
printf("\n");
}
return 0;
}
#include<stdio.h>
#include<string.h>
int main()
{
char a[10][10];
memset(a,'#',sizeof(a));
for(int i = 0;i < 10;i++)
{
for(int j = 0;j < 10;j++)
printf("%c ",a[i][j]);
printf("\n");
}
return 0;
}
memset是一个初始化函数,作用是将某一块内存中的全部设置为指定的值。
比直接赋值快一点
void *memset(void *s, int c, size_t n);
s指向要填充的内存块。
c是要被设置的值。
n是要被设置该值的字符数。
返回类型是一个指向存储区s的指针。
迷宫解决
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
struct node
{
int i, j;
string ans;
};
const int N = 30; // 地图的行数
const int M = 50; // 地图的列数
string map[500]; // 存储地图的字符串数组
char h[4] = {'D', 'L', 'R', 'U'}; // 方向对应的字符
string s;
int dx[4] = {1, 0, 0, -1}; // x 方向的移动
int dy[4] = {0, -1, 1, 0}; // y 方向的移动
void bfs()
{
node s ;
s.i = 0;
s.j = 0;
s.ans = "";
queue<node> q;
map[0][0] = '1'; // 将起点标记为已访问
q.push({0,0});
while(q.size())
{
node t = q.front(),b;
q.pop();
int x = t.i;
int y = t.j;
if (x == N-1 && y == M-1) // 到达终点
{
cout << t.ans << endl; // 输出路径
}
for(int i = 0 ; i < 4; i++) // 四个方向分别搜索
{
int xx = t.i + dx[i];
int yy = t.j + dy[i];
if(xx >= 0 && xx <= N-1 && yy >= 0 && yy <= M-1 && map[xx][yy] == '0')
{
map[xx][yy] = '1'; // 标记为已访问
b.ans = t.ans + h[i]; // 更新路径
b.i = xx;
b.j = yy;
q.push(b);
}
}
}
}
int main()
{
for(int i = 0 ; i < N ;i++) // 输入地图
{
cin >> map[i];
}
bfs(); // 开始搜索路径
return 0;
}
12/5
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
在算法竞赛中,我们经常能看到很多人写的代码中main()函数中第一行代码为:ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
这段代码的主要用途是在C++中关闭输入输出流的同步,以提高程序的执行效率。
具体而言,它的作用如下:
- 提高执行效率:默认情况下,C++的输入输出流与C标准库的输入输出函数是同步的,这会造成一定的性能损失。通过使用ios::sync_with_stdio(0)可以关闭这种同步,从而加快输入输出的速度,提高程序的执行效率。
- 解绑输入输出流:使用cin.tie(0)和cout.tie(0)可以取消cin与cout之间的绑定,这意味着在进行输入操作时,不需要强行刷新输出缓冲区。这样可以进一步提高程序性能。
注意事项:
- 不适用于混合输入输出:如果你的程序在输入输出中同时使用了C++的输入输出流和C标准库的输入输出函数(如scanf和printf),则不应该使用这段代码。因为这会导致输入输出之间的不同步。
- 不能混用输入输出函数:在使用了这段代码后,应避免使用C标准库的输入输出函数(如printf和scanf),因为这些函数与输入输出流的同步已被关闭。简单来说,关闭了同步流,就不能用scanf和printf。
- 不影响程序正确性:关闭输入输出流的同步不会影响程序的正确性,它只是为了提高程序的执行效率。因此,在一些对输入输出性能要求较高的场景下,可以考虑使用这段代码。
- 关闭了同步流(也就是使用这段代码),不能再用cout<<endl。而应该改用cout<<‘\n’。
因为通常情况下,cout<<endl会输出一个换行符并刷新输出缓冲区,确保内容立即显示。但是,当使用了上述代码时,cout<<endl不再具有自动刷新缓冲区的功能。
单调队列
411【模板】单调队列 滑动窗口最值 - 董晓 - 博客园 (cnblogs.com)
411【模板】单调队列 滑动窗口最值_哔哩哔哩_bilibili
#include <iostream>
using namespace std;
const int N = 1000010;
int a[N], q[N];
int main() {
int n, k; scanf_s("%d%d", &n, &k);
for (int i = 1; i <= n; i++) scanf_s("%d", &a[i]);
// 维护窗口最小值
int h = 1, t = 0; //清空队列
for (int i = 1; i <= n; i++) { //枚举序列
while (h <= t && a[q[t]] >= a[i]) t--; //队尾出队(队列不空且新元素更优)
q[++t] = i; //队尾入队(存储下标 方便判断队头出队)
if (q[h] < i - k + 1) h++; //队头出队(队头元素滑出窗口)
if (i >= k) printf("%d ", a[q[h]]); //使用最值
}
puts("");
// 维护窗口最大值
h = 1, t = 0;
for (int i = 1; i <= n; i++) {
while (h <= t && a[q[t]] <= a[i]) t--;
q[++t] = i;
if (q[h] < i - k + 1) h++;
if (i >= k) printf("%d ", a[q[h]]);
}
}
12/4
二进制数位判断是否为1
for (int j = 1; j< 30; ++j) //30位数可变其他数
if ((i >> j) & 1) //除以2 并取最后一位
++t;
for (int j = 1; j < 30; ++j):这是一个for循环,开始于j=1,每次循环j增加1,直到j等于30(不包括30)。if ((i >> j) & 1) ++t;:这是一个if判断语句。
(i >> j):这是右移运算符。它将数字i的二进制表示向右移动j位。例如,如果i是二进制的1101(十进制的13),那么i >> 2将得到二进制的1(十进制的1)。& 1:这是按位与运算符。它将结果限制在1位。如果i >> j的结果为0或2(在二进制中,只有最低位为1),那么结果为0。否则,结果为1。++t;:这是一个自增运算符。它增加变量t的值。
因此,整个循环的意思是:对于每个j(从1到2),如果i右移j位后结果的最低位是1,则t自增1。这在处理二进制数和位运算时常见,特别是当你需要计算一个数字在二进制下有多少个1时。
判断n 转16进制是否只有A~F

bool judge(int n)
{
while (n)
{
int t = n % 16;
if (t < 10)
{
return false;
}
n /= 16;
}
return true;
}
二 八 十 十六进制直接输出

#include <iostream>
#include<bitset>
using namespace std;
int main() {
int num = 123; // 十进制数
cout << "十进制: " << dec << num << endl;
cout << "八进制: " << oct << showbase << num << endl;
cout << "十六进制: " << hex << showbase << num << endl;
cout << "二进制: " << bitset<8> (num) << endl; // 使用bitset来显示二进制,注意需要指定位数
return 0;
}

0x或0X前缀用于表示紧随其后的数字是十六进制数。0b或0B:二进制前缀,用于表示紧随其后的数字是二进制数。例如,0b1010代表二进制的10,等同于十进制的2。- 0
:八进制前缀,如果一个数字序列以0开头,则表示这是一个八进制数。例如,0123`代表八进制的123,等同于十进制的83。

最小公倍数
a*b == _ _gcd(a,b) * 最小公倍数
最小公倍数 = a * b / gcd();
int Lcm(int a, int b)//最小公倍数函数
{
return a / __gcd(a, b) * b;
}
两个数的乘积等于这两个数的最大公约数与最小公倍数的积
11/30
输入行的要求
getchar();//读取那个换行符
string str;
getline(cin,str);//读一整行
11/29
阶乘约数
#include<bits/stdc++.h>
using namespace std;
/*
约数
1.唯一分解定理
对于一个大于1的整数n,可以将n分解成一些质因数的幂次和。
2.约数定理
一个正整数的正约数个数等于他通过唯一分解定理分解出来的所有质因数的次幂+1后的累乘结果
并且,求阶乘约数的时候
通过举例可以发现,n!的分解质因子的幂次等于1-n的分解每个数的质因子的幂次的和。
所以如果求100!的约数个数,就可以将1-100中所有的数分解后幂次相加再相乘*/
int a[105];//存储质因子的幂次
bool fun(int n)
{
//判断质数
for(int k = 2;k * k <= n;k++)
{
if(n % k == 0)
{
return false;
}
}
return true;
}
int main()
{
//根据唯一分解定理:对于一个大于1的整数n,n可以分解质因数为一些质因子的幂次的和
//枚举1-100求出质因子
for(int i = 1;i <= 100;i++)
{
//求出质因子
int t = i;//被除数
for(int j = 2;j <= i;j++)
{
//判断因数
if(i % j == 0)
{
//判断质数
if(fun(j) == true)
{
//求出幂
int temp = 0;//幂次
while(t % j == 0)
{
t /= j;
temp++;//幂次计数
}
//累加次幂
a[j] += temp;
}
}
}
}
long long int cnt = 1;
//最后根据约数定理
//一个正整数n的正约数等于分解定理分解的所有质因子的幂次+1的累乘
for(int i = 1;i <= 100;i++)
{
a[i]++;
cnt *= a[i];
}
cout << cnt << endl;
return 0;
}
11/27
1LL
int temp=1LL*(pow(x,i)+pow(y,j)+pow(z,k));
long long temp=1LL*(pow(x,i)+pow(y,j)+pow(z,k));
在代码中,1LL * (pow(x, i) + pow(y, j) + pow(z, k)) 表示将幂和计算的结果与 1LL 相乘,保证了结果的类型为长整型。
sqrtl
sqrtl是一个数学函数,用于计算 long double 类型数的平方根。具体来说,它返回一个 long double 类型的数,该数是传入参数的平方根
10^17 开根号用6次

gcd(int a,int b)
int gcd(int a,int b)
{
//return b == 0? a:gcd(b,a%b);
return b? gcd(b,a%b):a;
}
11/25
优先队列 priority_queue
priority_queue 是 C++ STL 中的一个容器适配器,它提供了一个优先队列的实现,保证在队列的头部始终是优先级最高的元素。默认情况下,priority_queue 以大根堆的形式进行存储和操作。
priority_queue 的常用操作包括:
push(x):将元素x插入到队列中。pop():弹出队列头部元素。top():访问队列头部元素。empty():判断队列是否为空。size():返回队列中元素的数量。
可以通过构造函数对队列进行一些初始化,例如指定队列的容量、比较函数等。
以下是一个使用priority_queue实现堆排序的示例代码:
#include <iostream>
#include <queue>
using namespace std;
int main() {
int a[] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
int n = sizeof(a) / sizeof(int);
// 创建一个大根堆
priority_queue<int> q;
// 将所有元素插入队列
for (int i = 0; i < n; i++)
q.push(a[i]);
// 依次弹出队列中的元素,得到从小到大排序的结果
while (!q.empty()) {
cout << q.top() << " ";
q.pop();
}
cout << endl;
return 0;
}
在这个例子中,我们先创建一个大根堆 priority_queue<int> q,然后将所有元素插入到队列中。由于默认的比较函数为 less<int>,因此 priority_queue 中的元素会按照从大到小的顺序排列。最后,我们依次弹出队列中的元素,得到从小到大排序的结果。
priority_queue<Type, Container, Functional> 是 std::priority_queue 的模板参数列表。
Type:表示队列中存储的元素类型。Container:表示底层容器的类型,默认情况下使用std::vector作为底层容器,但也可以选择其他容器,如std::deque。Functional:表示比较函数的类型,默认情况下使用std::less<Type>作为比较函数,即大根堆,但也可以选择std::greater<Type>来实现小根堆。
以下是对每个参数的详细说明:
Type:指定队列中元素的类型。例如,如果将int作为Type,则队列中存储的是整数类型的元素。Container(可选):指定底层容器的类型。默认情况下,底层容器为std::vector,但你可以选择其他容器,如std::deque等。在 STL 中,容器必须提供push_back()、pop_back()和back()等操作,以便priority_queue正常工作。Functional(可选):指定比较函数的类型。默认情况下,使用std::less<Type>,即大根堆。如果要实现小根堆,可以使用std::greater<Type>。比较函数用于确定元素的优先级。
以下是使用不同参数的示例:
maxHeap:大根堆,底层容器为std::vector。默认情况下,使用元素的<运算符进行比较。minHeap:小根堆,底层容器为std::deque。使用greater<int>函数对象作为比较函数,对元素进行比较。customHeap:自定义堆,元素为结构体Node。Node结构体重载了<运算符,根据val字段的值进行比较。strHeap:自定义堆,元素为字符串。使用 lambda 表达式cmp作为比较函数,根据字符串的长度进行比较。
#include <iostream>
#include <queue>
using namespace std;
int main() {
// 大根堆,底层容器为 std::vector
priority_queue<int> maxHeap;
// 小根堆,底层容器为 std::deque
priority_queue<int, deque<int>, greater<int>> minHeap;
// 自定义结构体作为元素,使用默认的比较函数(大根堆)
struct Node {
int val;
bool operator<(const Node& other) const {
return val < other.val;
}
};
priority_queue<Node> customHeap;
// 使用自定义的比较函数(小根堆)
auto cmp = [](const string& s1, const string& s2) {
return s1.length() > s2.length();
};
priority_queue<string, vector<string>, decltype(cmp)> strHeap(cmp);
return 0;
}
在这个例子中,我们展示了几种不同的 priority_queue 的使用方式。可以根据需要选择适合的参数类型,以满足对优先队列的需求。
struct tmp1 //运算符重载<
{
int x;
tmp1(int a) {x = a;}
bool operator<(const tmp1& a) const
{
return x < a.x; //大顶堆
return x > a.x; //小顶堆
}
};
压缩矩阵
#include <iostream>
using namespace std;
typedef long long LL; // 定义一个别名 LL,代表 long long 类型
int main()
{
LL n, q; // 输入的行数和查询次数
cin >> n >> q; // 输入行数和查询次数
LL num; // 存储每次查询的数字
while (q--)
{
LL i = 0, j = 0; // 初始化行号和列号为 0
cin >> num; // 输入查询的数字
i = (num + 1) / 3 + 1; // 根据查询数字计算对应的行号
j = num - 2 * i + 3; // 根据行号计算对应的列号
cout << i << " " << j << endl; // 输出查询结果
}
return 0;
}
11/24
高精度算法
#include<iostream>
using namespace std;
int a[5000]; // 定义一个数组,用于存储阶乘结果
int main()
{
int t; // t表示测试用例数目
cin >> t;
while (t--)
{
// 初始化数组,防止上一次计算结果影响本次计算
for (int i = 1; i <= 1001; ++i)
a[i] = 0;
a[1] = 1; // 对于0!和1!,直接赋值为1
int n, i, j, k, m;
int p = 1, jw = 0; // p表示数组a的有效位数,jw表示进位
cin >> n >> m; // 输入n和m
// 计算n!,并将结果存入数组a中
for (i = 2; i <= n; ++i)
{
jw = 0;
for (j = 1; j <= p; ++j)
{
a[j] = a[j] * i + jw; // 逐位相乘,并加上前一位的进位
jw = a[j] / 10; // 计算当前位产生的进位
a[j] = a[j] % 10; // 当前位只保留个位数
}
while (jw > 0)
{
a[j] = jw % 10; // 将最高位的进位赋给下一位
jw /= 10;
j++;
}
p = j - 1; // 更新数组a的有效位数
}
// 统计m在n!中出现的次数
long long sum = 0; // sum表示m在n!中出现的次数,使用long long类型防止溢出
for (i = p; i >= 1; i--)
{
if (a[i] == m) // 如果当前位等于m,则sum加1
{
sum++;
}
}
cout << sum << endl; // 输出结果
}
return 0;
}
模板
#include <cstring>
#include <iostream>
#define maxn 3000
int f[maxn];
using namespace std;
int main()
{
int i, j, n;
cin >> n;
memset(f, 0, sizeof(f)); // 将其中内存置于0
f[0] = 1; // 初始置于1
for (i = 2; i <= n; i++)
{
int jinwei = 0; // 定义进位初始为0
for (j = 0; j < maxn; j++)
{
int s = f[j] * i + jinwei; // 乘法结果为乘完加之前的进位
f[j] = s % 10;
jinwei = s / 10; // 获得进位数
}
}
/*下面这部分为了获取有多少位是有用的*/
for (j = maxn - 1; j >= 0; j--)
if (f[j] != 0)
break;
for (i = j; i >= 0; i--)
{
cout << f[i];
}
}
11/22
next_permutation() 全排列
next_permutation()是一个函数,通常在编程语言中用于生成给定序列的下一个排列。它可以按照字典序(升序)生成给定序列的下一个排列,并将其更新为下一个排列。
具体而言,next_permutation()函数接受一个序列作为参数,并将该序列重排为下一个字典序更大的排列。如果没有下一个更大的排列,则将序列重排为最小的(升序)排列。该函数返回一个布尔值,指示是否成功生成了下一个排列。
下面是一个示例,展示了如何使用next_permutation()函数来生成给定序列的所有排列:
cppCopy Code#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int arr[] = {1, 2, 3};
// 生成并打印所有排列
do {
for (int i = 0; i < 3; i++) {
cout << arr[i] << " ";
}
cout << endl;
} while (next_permutation(arr, arr + 3));
return 0;
}
输出结果将是:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
这个例子展示了如何使用next_permutation()函数生成给定序列的所有排列,并将它们打印出来。每次调用next_permutation()函数时,原始数组会被修改为下一个排列,直到没有更多的排列可生成为止。
需要注意的是,next_permutation()函数在不同的编程语言和库中可能有略微不同的实现方式,但其基本功能是相似的:生成给定序列的下一个排列。
E-排列式_蓝桥杯算法必刷题(一) (nowcoder.com)
#include<bits/stdc++.h>
using namespace std;
int main(){
int n[9]={1,2,3,4,5,6,7,8,9};
do{
int x1=n[4];
int y1=n[5]+10*n[6]+100*n[7]+1000*n[8];
int sum1=n[3]+10*n[2]+100*n[1]+1000*n[0];
int x2=n[5]+10*n[4];
int y2=n[6]+10*n[7]+100*n[8];
int sum2=n[3]+10*n[2]+100*n[1]+1000*n[0];
if(sum1==x1*y1){
printf("%d = %d x %d\n",sum1,x1,y1);
}
if(sum2==x2*y2){
printf("%d = %d x %d\n",sum2,x2,y2);
}
}while(next_permutation(n,n+9));
return 0;
}
11/19
c++ string 转 int stoi
std::stoi 是 C++ 标准库中的一个函数,用于将字符串转换为整数。它可以将包含数字的字符串转换为对应的整数值。
以下是一个 std::stoi 的使用示例:
#include <string>
int main() {
std::string str = "12345";
int num = std::stoi(str);
std::cout << "转换后的整数值为: " << num << std::endl;
return 0;
}
在这个示例中,std::stoi 函数被用于将字符串 “12345” 转换为整数值 12345,然后将其打印到控制台上。
需要注意的是,如果输入的字符串不是有效的整数,std::stoi 将抛出 std::invalid_argument 或 std::out_of_range 类型的异常。因此,在使用 std::stoi 时,最好处理可能出现的异常情况。
还有to_string
11/18
*max_element ()
*max_element()是 C++ 标准库<algorithm>中的一个函数,用于找到容器中的最大元素。它返回指向容器中最大元素的迭代器,通过*操作符可以获取该迭代器指向的值。下面是一个简单的示例,演示了
*max_element()的用法:在这个示例中,
max_it是指向容器vec中最大元素的迭代器,通过*max_it可以获取最大值并输出。
#include <iostream>
#include <vector>
#include <algorithm>
int main() {
std::vector<int> vec = {3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5};
auto max_it = std::max_element(vec.begin(), vec.end()); // 找到最大元素的迭代器
int max_value = *max_it; // 通过*操作符获取最大值
std::cout << "最大值为: " << max_value << std::endl;
cout<<*element(vec.begin(),vec.end());
return 0;
}
直线的斜率和截距公式
确定一条直线
k=(double)(y1-y2)/(x1-x2);
b=(double)(x1*y2-x2*y1)/(x1-x2);
11/17
单词分析
#include <iostream>
#include <map>
using namespace std;
map<char, int> a; // 使用 map 来存储每个字母出现的次数
int main()
{
string s;
cin >> s; // 输入单词
for (int i = 0; i < s.size(); ++i)
{
a[s[i]]++; // 统计每个字母出现的次数
}
char ans; // 存储出现次数最多的字母
int max = 0; // 存储出现次数最多的字母的次数
for (auto i : a)
{
if (i.second > max)
{
max = i.second;
ans = i.first;
}
}
cout << ans << endl; // 输出出现最多的字母
cout << max << endl; // 输出出现最多的字母的次数
return 0;
}
时间显示
#include <iostream>
using namespace std;
typedef long long LL;
int main()
{
LL n;
cin >> n; // 输入以秒为单位的时间
n /= 1000; // 将时间转换为以秒为单位
int a, b, c;
c = n % 60; // 计算秒数
n /= 60;
b = n % 60; // 计算分钟数
n /= 60;
a = n % 24; // 计算小时数
// 输出格式化的时间
printf("%02d:%02d:%02d", a, b, c);
return 0;
}
11/15
蓝桥杯经典题目 进制 转换
#include <bits/stdc++.h> // 导入标准 C++ 库中的所有内容,通常不建议使用这种方式,因为会导致编译时间增加和可能出现命名冲突
using namespace std;
int convert2ten(int a, int num) // 将 a 进制转换为十进制
{
int b = 0; // 初始化结果为0
int t;
int i = 0;
while (num != 0)
{
t = num % 10; // 取出num的个位数
num = num / 10; // 将num右移一位
b += t * pow(a, i); // 将t乘以a的i次幂后加到结果上
i++; // 更新指数
}
return b; // 返回结果
}
int convert2other(int a, int num) // 将十进制转换为 a 进制
{
queue<int> mod; // 定义一个队列存储余数
int t;
while (num != 0)
{
t = num % a; // 求num除以a的余数
num = num / a; // 更新num为num除以a的商
mod.push(t); // 将余数压入队列
}
int b = 0;
int i = 0;
while (!mod.empty())
{
t = mod.front(); // 取出队首元素
mod.pop(); // 弹出队首元素
b += t * pow(10, i); // 将t乘以10的i次幂后加到结果上
i++; // 更新指数
}
return b; // 返回结果
}
int main()
{
cout << convert2ten(9, 2022); // 输出将9进制数2022转换为十进制的结果
return 0;
}
日期模拟题
#include <iostream>
using namespace std;
// 定义一个数组来表示每个月份的天数
int days[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
// 判断是否为闰年
bool is_leap(int y)
{
return y % 400 == 0 || (y % 4 == 0 && y % 100 != 0);
}
// 计算某一年某个月的天数
int daysofmonth(int y, int m)
{
if (m == 2)
return is_leap(y) ? 29 : 28; // 如果是闰年,返回29天,否则返回28天
else
return days[m]; // 其他月份直接查表返回对应天数
}
int main()
{
int y = 2000, m = 1, d = 1, w = 6; // 初始化年、月、日和星期几
int ans = 0; // 初始化答案为0
while (y != 2020 || m != 10 || d != 2) // 循环直到日期达到 2020 年 10 月 2 日
{
if (d == 1 || w == 1)
ans += 2; // 如果是每月的第一天或者星期一,答案加2
else
ans++; // 否则答案加1
d++; // 天数加1
if (d > daysofmonth(y, m)) // 如果天数超过了这个月的天数
{
d = 1; // 天数重置为1
m++; // 月份加1
}
if (m > 12) // 如果月份超过12
{
m = 1; // 月份重置为1
y++; // 年份加1
}
w++; // 星期几加1
if (w == 8)
w = 1; // 如果超过7,重置为1
}
cout << ans << endl; // 输出答案
return 0;
}
11/14
并查集
int n = 1005; // n根据题目中节点数量而定,一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}
// 并查集里寻根的过程
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}
// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return u == v;
}
// 将v->u 这条边加入并查集
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[v] = u;
}
通过模板,我们可以知道,并查集主要有三个功能。
- 寻找根节点,函数:find(int u),也就是判断这个节点的祖先节点是哪个
- 将两个节点接入到同一个集合,函数:join(int u, int v),将两个节点连在同一个根节点上
- 判断两个节点是否在同一个集合,函数:isSame(int u, int v),就是判断两个节点是不是同一个根节点
10/29
欧拉函数和快速幂
欧拉函数
LL t = (n - 1) % (P - 1) * ((m - 1) % (P - 1)) % (P - 1);
欧拉函数(Euler’s totient function),也称为 phi 函数,用符号 φ(n) 表示,表示小于等于 n 的正整数中与 n 互质的数的个数。例如,φ(6) = 2,因为小于等于 6 的正整数中,与 6 互质的数是 1 和 5。
欧拉函数的计算可以使用以下算法:
- 首先,将 φ(n) 的初始值设为 n。
- 然后,对于 n 的每个质因子 p,将 φ(n) 减去 φ(n) / p。
- 最后,返回计算得到的 φ(n) 值。
这个算法的时间复杂度取决于分解质因数的速度。如果使用 trial division 等较慢的方法分解质因数,则时间复杂度为 O(√n log n);如果使用更快的分解质因数算法,如 Pollard-Rho 算法或 ECM 算法,则时间复杂度可能更低。
下面是一个使用 trial division 分解质因数的欧拉函数计算算法的示例代码:
在这个算法中,我们从 2 开始枚举每个质数 i,如果 n 可以被 i 整除,则将 φ(n) 减去 φ(n) / i,并重复除以 i 直到不能整除为止。最后,如果 n 大于 1,则说明 n 是一个大于 √n 的质因子,将 φ(n) 减去 φ(n) / n。最终返回计算得到的 φ(n) 值。
需要注意的是,在实际使用中,为了提高计算速度,可以预处理出小于等于某个数 N 的所有欧拉函数值,存储在数组中,以便快速查询。
int euler_phi(int n) {
int res = n;
for (int i = 2; i * i <= n; i++) {
if (n % i == 0) {
res -= res / i;
while (n % i == 0) n /= i;
}
}
if (n > 1) res -= res / n;
return res;
}
快速幂
LL qmi(LL a, LL b, LL p)
{
LL res = 1;
while (b)
{
if (b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
ll ksm( ll a, ll b)
{
ll res = 1;
while(b)
{
if(b & 1) res = res * a % mod;
a = a * a % mod;
b>>=1;
}
return res %mod;
}
这段代码实现了快速幂算法(Fast Power Algorithm),用于计算 a 的 b 次方对 p 取模的结果。
函数
qmi的参数说明如下:
a:底数b:指数p:模数
在函数内部,使用一个变量
res来保存最终的结果,初始值为 1。然后通过一个循环,不断地将底数a进行平方并对模数p取模,同时将指数b右移一位(相当于除以 2)。在每次循环中,通过判断指数
b的最低位是否为 1(即b & 1是否为真),来决定是否将当前的底数a乘到结果res上。如果最低位为 1,则将res乘以a并对p取模。最后,当指数
b变为 0 时,循环结束,函数返回最终的结果res。这个算法的时间复杂度为 O(log b),其中 b 是指数的大小。它通过将指数
b转化为二进制形式进行迭代计算,避免了对指数进行逐个相乘的操作,从而提高了计算效率。
总结:先判断b是否是奇数还是偶数,返回ans









 浙公网安备 33010602011771号
浙公网安备 33010602011771号