洛谷P1670 题解

题意简述

给定一个有 \(n\) 个节点的树，要求输出所有的节点 \(u\) 使得当这棵树以 \(u\) 为根的时候，其儿子为根的子树大小小于节点数 \(n\) 的一半。如果没有这样的 \(u\) 输出 NONE。

思维路径

首先考虑计算子树大小，使用 dfs 遍历一遍即可，时间复杂度为 \(O(n)\)，如果枚举每一个节点作为根则复杂度达到 \(O(n^2)\)，对于本题来说太大，因此我们需要更好的优化方案。

由此可见，我们大概率只会进行一次 dfs 遍历。我们将样例的图画出来，进行研究。

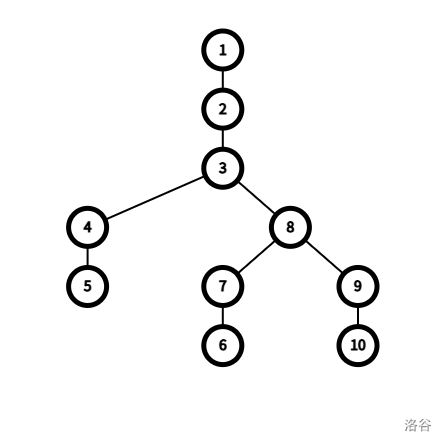
考虑到 3 号点是一个答案，我们以它为例研究，在下图中我标出了需要与 \(n/2\) 比较大小的子树。

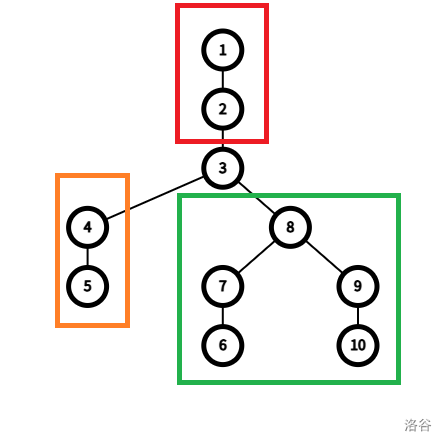
观察可见，橙框和绿框中的子树大小就是以 \(1\) 为根时子树大小，不必另外计算，而红框中的节点数恰好为总节点数 \(n\) 减去 \(3\) 号点的子树大小。通过这种方法即可仅用一次 dfs 计算出所有需要的数值。

随后遍历每个点是否符合条件即可，这个步骤也可以与 dfs 本身合并。

AC 代码

#include<bits/stdc++.h>
using namespace std;
const int N=10009;
int n,ok[N],ans,sz[N];
vector<int> es[N];

void input(){
	cin>>n;
	for(int i=1;i<n;i++){
		int u,v;
		cin>>u>>v;
		es[u].push_back(v);
		es[v].push_back(u); 
	}
}

void dfs(int u,int fa){
	for(int i=0;i<es[u].size();i++){
		int v=es[u][i];
		if(v==fa) continue;
		dfs(v,u);
		sz[u]+=sz[v];
		if(sz[v]>n/2) ok[u]=0;
	} 
	sz[u]++;
	if(n-sz[u]>n/2) ok[u]=0;
}

void solve(){
	for(int i=1;i<=n;i++) ok[i]=1; 
	dfs(1,0);
	for(int i=1;i<=n;i++){
		if(ok[i]){
			cout<<i<<"\n";
			ans++;
		}
	}
	if(!ans) cout<<"NONE";
}

int main(){
	input();
	solve();
	return 0;
}