tarjan求边双连通分量

点双连通分量见tarjan求点双连通分量
部分参考 lyd《算法竞赛进阶指南》

前置概念

给定无向图 \(G=(V,E)\)

• 桥（割边）：若 \(e \in E\)，如果删去 e 后图分裂成两个子图，那么 e 这条边就为桥（割边）。
• 时间戳：在深度优先访问时按照每个节点第一次被访问的时间顺序，依次给予 \(1\) ~ \(N\) 的标记，记为 \(dfn\) 数组。
• 搜索树：任选一个节点出发深度优先搜索，每个节点访问一次，所有发生递归的边组成的树。举例来说：图中红色的边即为搜索树中的一种，搜索树不唯一。
  
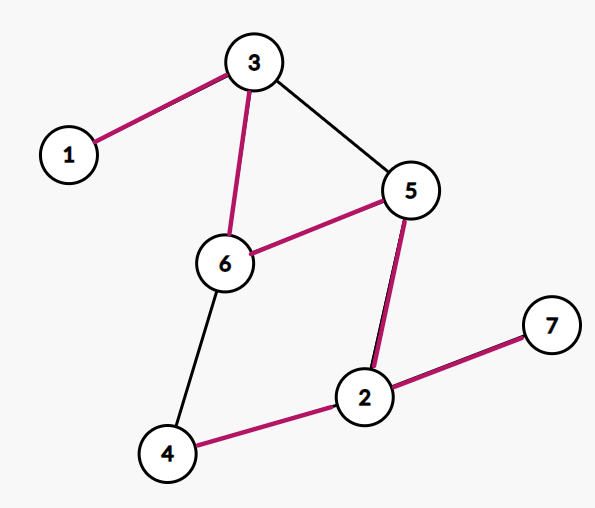
• 追溯值：记为 \(low\) 数组，定义为以下节点中的最小值：
  1.subtree中的节点。
  2.通过一条不在搜索树上的边能够到达subtree的节点。
• 边双连通图：一张不存在桥的无向连通图。
• 边双连通分量：简记为 “e-DCC”，表示无向连通图的极大边双连通子图。

追溯值的求法

1. 先令 low[x]=dfn[x]
2. 若在搜索树上，x 为 y 的父节点，则 low[x]=min(low[x],low[y])。
3. 若无向边 (x,y) 不是搜索树上的边，则 low[x]=min(low[x],dfn[y])。

割边（桥）的判定方法

若无向边 (x,y) 为桥，则 x,y 应当满足以下条件：

1. 边 (x,y) 在搜索树上
2. 令 y 为 x 的子节点，那么 dfn[x]<low[y]

原理：
当dfn[x]<low[y]时，表示 y 及其子树上的点无法通过除 (x,y) 以外的边到达其他点，也就是说，若 (x,y) 不存在，那么 y 及其子树无法与其他部分连通，那么 (x,y) 满足桥的定义，即确认 (x,y) 为桥。

例：P1656 炸铁路
很明显，题目中的 key road 就表示割边，这是一道典型的求所有割边的模板
（他的数据范围小到可以枚举，但是不妨碍它是一道求割边的模板）

My code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll M=5009;
const ll N=159;
ll n,m;
struct edge{
	ll to,nxt;
	bool bridge;
} e[M<<1];
struct ANS{
	ll from,to;
} ans[M];
ll nA;
ll hd[N],nE=1;
ll dfn[N],low[N],timer;

void add(ll u,ll v){
	e[++nE]=(edge){v,hd[u],false};
	hd[u]=nE;
}

void input(){
	cin>>n>>m;
	for(ll i=1;i<=m;i++){
		ll u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
}

void dfs_tarjan(ll u,ll in_edge){
	dfn[u]=low[u]=++timer;
	for(ll i=hd[u];i;i=e[i].nxt){
		ll v=e[i].to;
		if(!dfn[v]){
			dfs_tarjan(v,i);
			low[u]=min(low[u],low[v]);
			if(dfn[u]<low[v]){
				e[i].bridge=true;
				e[i^1].bridge=true;
			}
		}
		else if(i!=(in_edge^1)){
			low[u]=min(low[u],dfn[v]);
		}
	}
}

bool cmp(const ANS&a,const ANS&b){
	if(a.from<b.from) return true;
	else if(a.from>b.from) return false;
	else if(a.to<b.to) return true;
	else return false;
}

void solve(){
	for(ll i=1;i<=n;i++){
		if(!dfn[i]) dfs_tarjan(i,0);
	}
	for(ll i=2;i<=nE;i+=2){
		if(e[i].bridge){
			ans[++nA]=(ANS){min(e[i].to,e[i^1].to),max(e[i].to,e[i^1].to)};
		}
	}
	sort(ans+1,ans+nA+1,cmp);
	for(ll i=1;i<=nA;i++){
		cout<<ans[i].from<<" "<<ans[i].to<<endl;
	} 
}

int main(){
	input();
	solve();
	return 0;
}
 

边双连通分量的求法

将一张无向图中的所有桥删去后，无向图会分成若干个连通块，每一个连通块就是一个边双连通分量。
具体来说，在求桥的过程中，我们已经对所有桥的边进行了标记。再次深度优先搜索，不访问桥，对每一各连通块进行标记，则可以得到边双连通分量。

例：P8436 【模板】边双连通分量
模板题

My code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=500009;
const ll M=2000009; 
ll n,m;
struct edge{
	ll to,nxt;
	bool bridge;
} e[M<<1];
ll hd[N],nE=1;
ll dfn[N],low[N],timer;
ll clr[N],dcc;
vector<ll> ans[N];

void add(ll u,ll v){
	e[++nE]=(edge){v,hd[u],false};
	hd[u]=nE;
}

void input(){
	cin>>n>>m;
	for(ll i=1;i<=m;i++){
		ll u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
}

void dfs_tarjan(ll u,ll in_edge){
	dfn[u]=low[u]=++timer;
	for(ll i=hd[u];i;i=e[i].nxt){
		ll v=e[i].to;
		if(!dfn[v]){
			dfs_tarjan(v,i);
			low[u]=min(low[u],low[v]);
			if(dfn[u]<low[v]){
				e[i].bridge=true;
				e[i^1].bridge=true;
			}
		}
		else if(i!=(in_edge^1)){
			low[u]=min(low[u],dfn[v]);
		}
	}
}

void dfs_clr(ll u){
	clr[u]=dcc;
	ans[dcc].push_back(u);
	for(ll i=hd[u];i;i=e[i].nxt){
		if(e[i].bridge) continue;
		ll v=e[i].to;
		if(clr[v]) continue;
		dfs_clr(v);
	}
}

void solve(){
	for(ll i=1;i<=n;i++){
		if(!dfn[i]){
			dfs_tarjan(i,0);
		}
	} 
	for(ll i=1;i<=n;i++){
		if(!clr[i]){
			dcc++;
			dfs_clr(i);
		}
	}
	cout<<dcc<<endl;
	for(ll i=1;i<=dcc;i++){
		cout<<ans[i].size()<<" ";
		for(ll j=0;j<(ll)ans[i].size();j++){
			cout<<ans[i][j]<<" ";
		}
		cout<<endl;
	}
}

int main(){
	input();
	solve();
	return 0;
} 

完结撒花thx~