JZOJ 4308.长寿花

题面

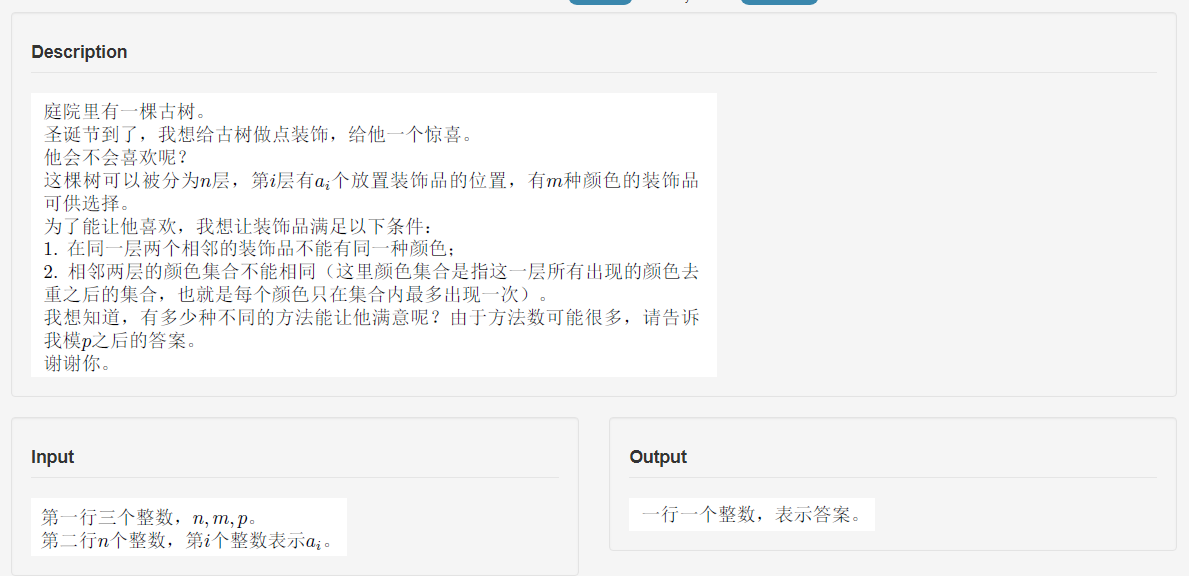
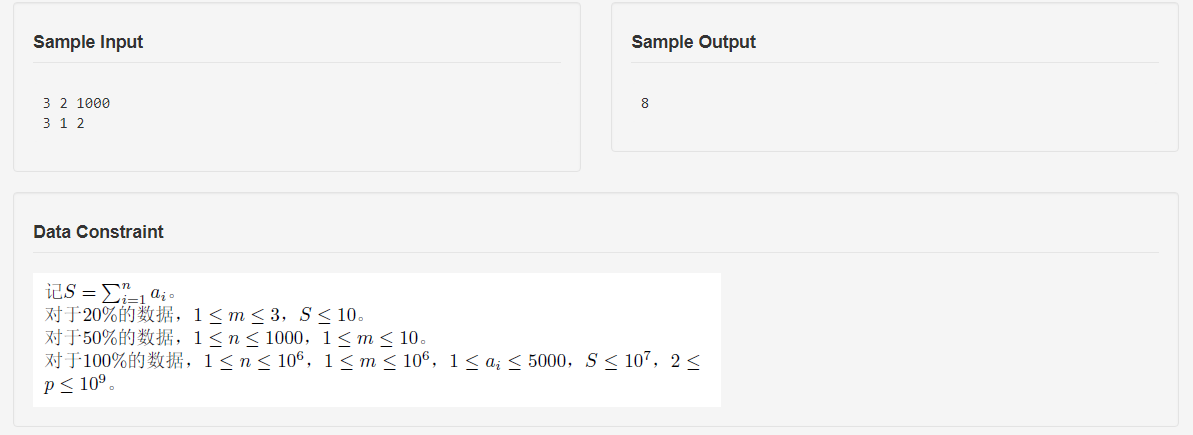
思路

这种题当然要 \(dp\) 啦
设 \(g_{i,j}\) 表示前 \(i\) 个位置用指定的 \(j\) 种颜色装饰（即用颜色 \(1..j\) 来装饰）
那么 \(g_{i,j}=g_{i-1,j}*(j-1)+g_{i-1,j-1}*j\)
前一项表示前 \(i-1\) 用了 \(j\) 种颜色，那么当前位可以用 \(j-1\) 种颜色，因为它和前面一个不能相同
后一项表示前 \(i-1\) 用了 \(j-1\) 种颜色，根据定义，前 \(i-1\) 位用的颜色是 \(1..j-1\)，而现在多了一种来用，那么在 \(i\) 这个阶段的前 \(i-1\) 位用 \(j-1\) 种颜色可供选择的方案是 \(\binom{j}{j-1}\)，即 \(j\) 种方案。选完后第 \(i\) 位就确定了，那么总的方案就是颜色选择方案乘上 \(g_{i-1,j-1}\)，后者可称为排法

再设 \(f_{i,j}\) 表示前 \(i\) 层放了装饰品且第 \(i\) 层选 \(j\) 种颜色的装饰品的方案数
那么 \(f_{i,j}={\sum_{k=1}^{a_{i-1}}f_{i-1,k}*C_{m}^{j}*g_{a_i,j}}-f_{i-1,j}*g_{a_i,j}\)
意思是前 \(i-1\) 层放的方案乘上本层 \(a_i\) 个位置选 \(j\) 种颜色的方案（乘法原理），因为 \(g\) 此前的定义是给定的 \(j\) 种颜色，然而在 \(f\) 中我们可以任意选 \(j\) 种，故要乘上 \(C_{m}^{j}\)
而题中规定本层与上一层颜色去重后的集合不能相同，所以我们再减去 \(f_{i-1,j}*g_{a_i,j}\) 即为前一个式子重复算的数量

而本题更恶心的是模数不一定是质数，所以再算组合数时我们需要质因数分解，加点奇技淫巧避免时间和空间裂开
看我们算 \(C\) 的过程，显然算 \(C_{m}^{j+1}\) 时可以从 \(C_{m}^j\) 处推来
所以我们分解质因数后存的东西不用清零，直接指数该加的加，该减的减
最后快速幂算一下剩下的指数和底数的贡献就行了

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
typedef long long LL;

const int M = 5005;
int n , m , a[1000005] , Mx , o , tot , pr[M] , vis[1000005] , num[1000005] , s[1000005] , cnt;
LL p , g[M][M] , f[3][M] , c[1000005] , sum , ans;

inline void getprime(int m)
{
	vis[0] = vis[1] = 1;
	for(register int i = 2; i <= m; i++)
	{
		if (!vis[i]) pr[++tot] = i;
		for(register int j = 1; j <= tot && pr[j] * i <= m; j++)
		{
			vis[pr[j] * i] = 1;
			if (i % pr[j] == 0) break;
		}
	}
}

inline LL fpow(LL x , int y)
{
	LL res = 1;
	while (y)
	{
		if (y & 1) res = res * x % p;
		y >>= 1 , x = x * x % p;
	}
	return res;
}

inline void up(int x)
{
	for(register int i = 1; i <= tot && pr[i] * pr[i] <= x; i++)
	if (x % pr[i] == 0)
	{
		if (!vis[pr[i]]) vis[pr[i]] = 1 , num[++cnt] = pr[i];
		while (x % pr[i] == 0) s[pr[i]]++ , x = x / pr[i];
	}
	if (x > 1)
	{
		if (!vis[x]) num[++cnt] = x , vis[x] = 1;
		s[x]++;
	}
}

inline void down(int x)
{
	for(register int i = 1; i <= tot && pr[i] * pr[i] <= x; i++)
	if (x % pr[i] == 0)
	{
		while (x % pr[i] == 0) s[pr[i]]-- , x = x / pr[i];
	}
	if (x > 1) s[x]--;
}

inline LL getc(int x , int y)
{
	LL res = 1;
	up(y) , down(x);
	for(register int i = 1; i <= cnt; i++)
		res = res * fpow((LL)num[i] , s[num[i]]) % p;
	return res;	
}

int main()
{
	freopen("kalanchoe.in" , "r" , stdin);
	freopen("kalanchoe.out" , "w" , stdout);
	scanf("%d%d%lld" , &n , &m , &p);
	for(register int i = 1; i <= n; i++) scanf("%d" , &a[i]) , Mx = max(Mx , a[i]);
	
	g[1][1] = 1;
	for(register int i = 2; i <= Mx; i++)
		for(register int j = 1; j <= i; j++)
			g[i][j] = (g[i - 1][j] * (j - 1) % p + g[i - 1][j - 1] * j % p) % p;
	
	getprime(m + 3);
	memset(vis , 0 , sizeof vis);
	
	for(register int i = 1; i <= min(m , Mx); i++) c[i] = getc(i , m - i + 1);
	
	sum = 1;
	for(register int i = 1; i <= n; i++)
	{
		o = 1 - o;
		for(register int j = 1; j <= min(a[i] , m); j++) 
			f[o][j] = ((sum * c[j] % p * g[a[i]][j] % p - f[1 - o][j] * g[a[i]][j] % p) % p + p) % p;
		sum = 0;
		for(register int j = 1; j <= min(a[i] , m); j++) sum = (sum + f[o][j]) % p;
		if (i > 1) for(register int j = a[i] + 1; j <= a[i - 2]; j++) f[o][j] = 0; 
	}
	for(register int i = 1; i <= min(a[n] , m); i++) ans = (ans + f[o][i]) % p;
	printf("%lld" , ans);
}