图之拓扑排序问题

这篇文章用来复习拓扑排序问题.
拓扑排序是对无圈图的顶点的一种排序,它使得若存在一条从u_i到u_j的路径,那么在排序中u_j就会出现在u_i的后面.

引用wiki的描述:
In the field of computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge uv from vertex u to vertex v, u comes before v in the ordering.

一个简单的求拓扑排序的算法是先找出任意一个没有入边的顶点.然后显示出该顶点,并将它和它的边一起从图中删除,然后对图的其余部分用同样的方法处理.

例如:

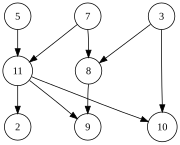
它的输出顺序可以为

5, 7, 3, 11, 8, 2, 9, 10

3, 5, 7, 8, 11, 2, 9, 10

5, 7, 3, 8, 11, 10, 9, 2

7, 5, 11, 3, 10, 8, 9, 2

5, 7, 11, 2, 3, 8, 9, 10

3, 7, 8, 5, 11, 10, 2, 9

可以发现顺序不是唯一的,但是都满足顶点的先后关系.

实现:

我使用了邻接矩阵来存储图,因为我当时认为这样可以方便查找顶点的入度(其实还有其他办法)

void CGraph::topologySort(){
	int indegreeIsZeroIndex = -1;
	// 寻找入度为0的点
	while ((indegreeIsZeroIndex = findIndegreeIsZero()) != -1)
	{
    	// 输出此顶点
		std::cout <<indegreeIsZeroIndex <<" ";
		// "移除"入度为0的点
		removeOutdegree(indegreeIsZeroIndex);
		// 标记为已访问
		setVertexState(indegreeIsZeroIndex,VISITED);
	}
	std::cout <<std::endl;
    // 判断是否有环
    for (int i = 0; i < vertexNum; i++)
	{
		if (visited[i] == NOVISIT)
		{
			std::cout <<"图中至少有一个环"<< std::endl;
			break;
		}
	}
}

使用场景:

• 拓扑排序可以用来检测图中是否有环
• 用来确定一个依赖关系中事物的发生的顺序
• ...

关于拓扑排序:

• 进一步优化
  还可以使用队列,将所有入度为0的顶点放入其中,此时负责查找入度为0的顶点的函数返回并删除队列中的顶点,当降低它的邻接顶点的入度时,检查它的入度,只要入度为0,就可以把该顶点放入队列中.

// 还可以使用队列,将所有入度为0的顶点放入其中
for each vertex V
	if (Indegree[v] == 0)
    	Enqueue(v,Q)

while (! IsEmpty (Q))
{
	//此时负责查找入度为0的顶点的函数返回并删除队列中的顶点
	v = Dequeue (Q);
    TopNum[v] = ++ counter;
    //当降低它的邻接顶点的入度时,检查它的入度,只要入度入为0,就可以把该顶点放入队列中
    for each w adjacent to V:
		if (-- Indegree[w])
			Enqueue(w,Q)
}
if (counter != NumVertex)
	Error ("图中有环");

• 时间复杂度
  若使用邻接表和队列的结合,那么使用这个算法所用的时间为O(E + V),当认识到for循环对每条边顶多执行一次的时,这个结果是明显的.队列操作对每个顶点最多进行一次,而初始化所花费的时间也和图的大小成正比.

详细代码请见我的github
但是这个实现的比较笨拙 😦